Тригонометрические уравнения

1.

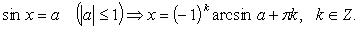
Частные случаи

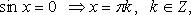
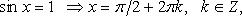
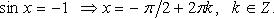
2.

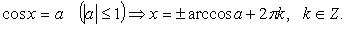
Частные случаи

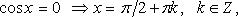
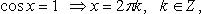
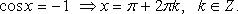
3.

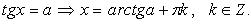
Частные случаи

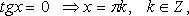
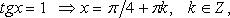
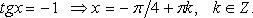
4.

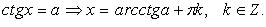
Частные случаи

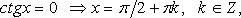
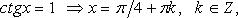
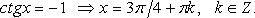
1.

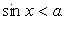
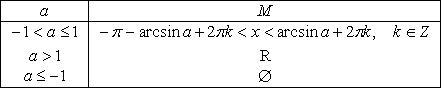
2.

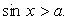
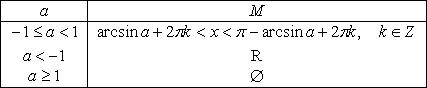
3.

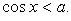
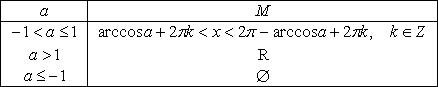
4.

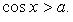
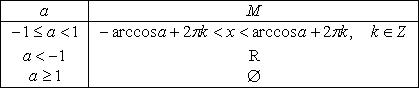
5.

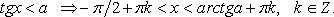
6.

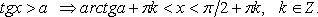
7.

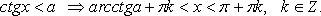
8.

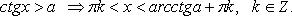
Функции arcsin a, arctg a являются нечетными; функции arccos a,

arcctg a не являются четными, не являются нечетными.

Для тригонометрических уравнений не существует единого метода

решения. В каждом конкретном случае успех определяется, в частности,

знанием тригонометрических формул и навыками решения задач.

Необходимо помнить следующие моменты:

При решении тригонометрических уравнений нельзя сокращать на

переменную величину, это может привести к потере корней уравнения.

Необходимо каждый множитель исследовать на решение.

2. При решении тригонометрических уравнений необходимо учитывать

область допустимых значений (О.Д.З.).

3. При возведении обеих частей уравнения в четную степень могут

появляться посторонние корни. Необходима отборка полученных

решений, но это сложно, поэтому по возможности нужно обходиться

без этой операции.

4. Потеря корней уравнения может произойти и от замены

тригонометрических функций через тангенс x = t 2tg − универсальная

тригонометрическая подстановка. Тогда sin x = ; 12 1 tg ( / 2) 2tg( / 2)

Функция tg (х/2) не существует для х/2 = π/2 + πn, т.е. х ≠ π +

2πn. Но sin x и cos x определены в этих точках. Поэтому необходимо

всегда проверять корни х = π + 2πn на решение отдельно.

o Простейшие тригонометрические уравнения.

o Уравнение sin x = a

Если | a | > 1, то уравнение sin x = a не имеет корней. Например, уравнение sin x = 2 не имеет корней.
Если | a | ≤ 1, то корни уравнения выражаются формулой x = ( —1)ⁿ arcsin a + πn, n ∈ Z.
Частные случаи:
1. sin x = 0 ⇒ x = πn, n ∈ Z.
2. sin x = 1 ⇒ x = π/2 + 2πn, n ∈ Z.
3. sin x = -1 ⇒ x = -π/2 + 2πn, n ∈ Z.

o Уравнение cos x = a

Если | a | > 1, то уравнение cos x = a не имеет корней. Например, уравнение cos x = —1,5 не имеет корней.
Если | a | ≤ 1, то корни уравнения выражаются формулой x = ±arccos a + πn, n ∈ Z.
Частные случаи:
1. cos x = 0 ⇒ x = π/2 + πn, n ∈ Z.
2. cos x = 1 ⇒ x = 2πn, n ∈ Z.
3. cos x = -1 ⇒ x = π + 2πn, n ∈ Z.

o Уравнение tg x = a

Уравнение tg x = a имеет корни при любом значении a. Корни уравнения выражаются формулой x = arctg a + πn, n ∈ Z.

o Уравнение ctg x = a

Уравнение ctg x = a имеет корни при любом значении a. Корни уравнения выражаются формулой x = arcctg a + πn, n ∈ Z.