Де γ – контур, що охоплює всі полюсы функції X(z). Співвідношення(3.8) зворотне Z- перетворення.

Приклад: Нехай задане Z- перетворення вхідного сигналу.

Потрібно знайти вихідний сигнал.

Функція x(z) (x(z)=(z+1)/z) аналитична на всій площині, за винятком т. z=0. Звертаючи до формули (3.8), знайдемо:

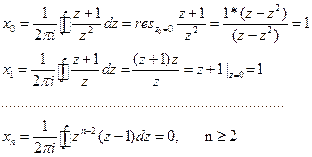
Вихідний сигнал має вид x(n)=(1,1,0,0,0,…)...

Розглянемо найважливіші властивості Z-перетворення: вони аналогічні властивостям Лапласа:

1) Лінійність.

Якщо X₁(n) і X₂(n) – числові послідовності, що відображають дискретні сигнали Z-перетворення, що мають, _X1(z) і _X2(z), то лінійна комбінація сигналів

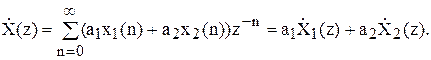X₃(n)=a₁x₁(n)+a₂x₂(n) має Z-перетворення у виді лінійної комбінації їхніх Z-перетворень.

2) Теорема зсуву. (Z-перетворення зміщеного сигналу)

Нехай x₂(n) отриманий з x₁(n) зсувом останнього убік запізнювання на одну позицію: x₂(n)=x₁(n-1).

Безпосереднє обчислення Z-перетворення приводить до результату:

X₂(z)=x₁(z)z^-1, при запізнюванні на m позицій:

X₂(z)=x₁(z)z^-m, еквівалентно множенню перетворення на z^-m.

3) Теорема про згорток.

Z-перетворення дискретної згортки 2-х послідовностей дорівнює добутку Z-перетворень цих послідовностей:

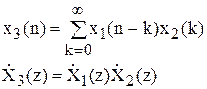
На підставі викладених властивостей сформулюємо алгоритм аналізу ЛЦФ методом Z-перетворення.

Користаючись теоремою про згорток, можна записати Z-перетворення вихідного сигналу через добуток Z-перетворень вхідного сигналу й імпульсної характеристики ЛЦФ.

Визначення. Z-перетворення імпульсної характеристики називають передатною функцією ЛЦФ чи його системною функцією.

За аналогією з рівнянням згортки сигналів у часовій області

для перебування вихідної послідовності Y(z)=G(z)X(z) необхідно визначити:

1) Z-перетворення вхідної послідовності x(n)

2)
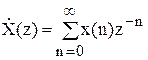
Передатну функцію G(z) по відомій імпульсній характеристиці g(n)

3)
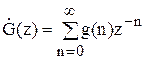
Z-перетворення вихідної послідовності

4)
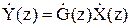
Саму вихідну послідовність

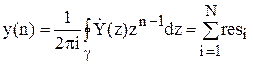
за допомогою теореми про лишки.

Способи визначення передатної функції ЛЦФ.

1) Прямим Z-перетворенням імпульсної характеристики ЛЦФ:

2)
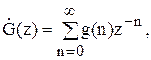
По різницевому рівнянню.

Нехай рекурсивний ЛЦФ описується різницевим рівнянням виду:

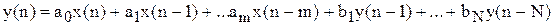
Застосувавши до рівняння Z-перетворення, одержимо.

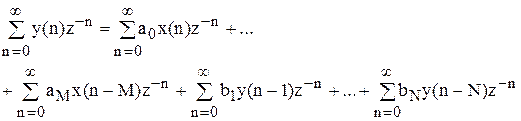
кожна з напівнескінченних сум дорівнює: (користаючись властивістю лінійності і теоремою зсуву)

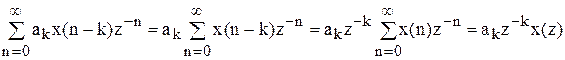
для трансверсальної частини суми.

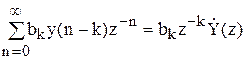
для рекурсивної частини суми.

Таким чином, Z-перетворення різницевого рівняння:

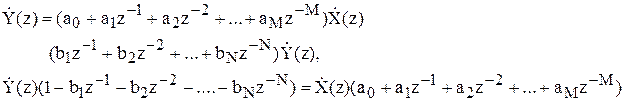
Маємо передатну функцію ЛЦФ:

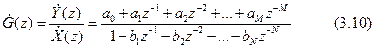
Вираження (3.10) має велике значення, тому що зв'язуючи передатну функцію і різницеве рівняння ЛЦФ, дозволяє вирішити також і зворотню задачу – по передатній функції ЛЦФ G(z) знайти його різницеве рівняння і по ньому побудувати структурну схему фільтра. Задачі подібного типу (установлення структури по характеристиках) звуться задач синтезу, чи в даному випадку задач реалiзацii ЛЦФ.

По вираженню типу (3.10) будується різницеве рівняння виду

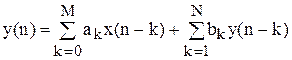
Приклад: Реалізуємо фільтр із передатною функцією

G(z)=(2z^-1+1)/(4z^-2+4z^-1+2).

Розділивши вираження на коефіцієнт при z^-1 у чисельнику, маємо

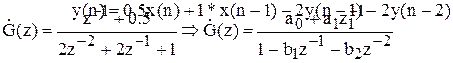
Тобто M=1; a₀=0.5; a₁=1; N=2; b₁=-2; b₂=-2, і

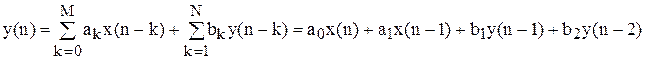Побудуємо по різницевому рівнянню структурну схему ЛЦФ.

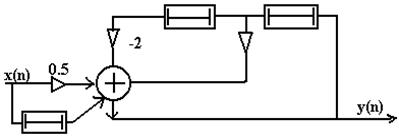Рис.3.1

Приклад. Знайдемо вихідний сигнал методом Z-перетворення побудованого ЛЦФ. Подамо на його вхід послідовність x(n)=(1/2)ⁿ і визначимо y(n).

1) Z-перетворення вхідної послідовності

2)
Як пам'ятаємо, передатна функція

3)
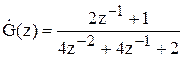
Z-перетворення вхідного сигналу:

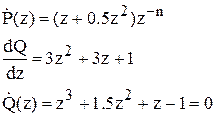4) Вихідна послідовність сигналу:

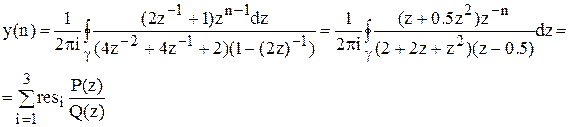
Знайдемо полюси підінтегральної функції – корені знаменника: 2+2z+z²=0,

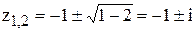z-0.5=0, тоді z₃=0.5

Знайдемо лишки:

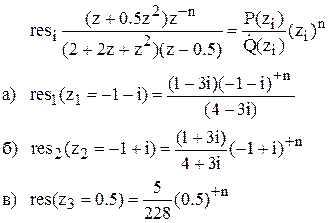
Представляючи комплексні числа в показовій формі *ρe^iφ знайдемо

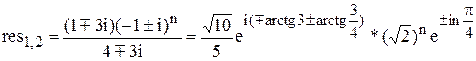
Вихідна послідовність як сума лишкiв res₁, res₂, res₃ дорівнює:

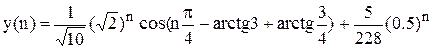
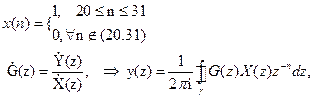Знайти y(n), якщо

Приклад Нехай дана передатна функція ЛЦФ у виді

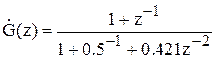
хоча легше в даному випадку побудувати y(n) по різницевому рівнянню, користаючись передатною функцією:

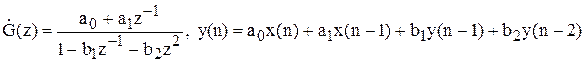
y(n)=x(n)+1*x(n-1)-0.5y(n-1)-0.421y(n-2)

Побудуємо структурну схему ЛЦФ по різницевому рівнянню.

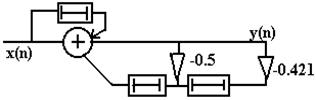Рис.3.2

Розрахунок ЛЦФ (перетворення y(n) по x(n)) можна реалізувати у виді програми розрахунку y(n) по різницевому рівнянню, задаючи у виді масиву x(n) – вхідну послідовність і знаходячи масив y(n) – вихідну послідовність.