Моменты инерции сечения
В дальнейшем при изучении деформаций изгиба и кручения придется пользоваться новыми геометрическим характеристиками — моментами инерции сечения.
Осевым моментом инерции сечения относительно данной оси называется сумма произведений элементарных площадей dА на квадрат их расстояний до данной оси (например, х или у), которая распространяется на всю площадь сечения А.
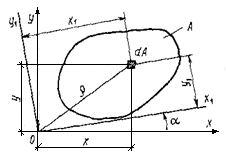
Рисунок 2.2.3
Так, осевые моменты инерции (рис.2.2.3) относительно осей х и у равны:
; 
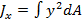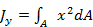(2.2.4)
Полярным моментом инерции сечения относительно данной точки (полюс 0) называется сумма произведений элементарных площадей dА на квадраты их расстояний до этой точки, которая распространяется на всю площадь сечения А.
Следовательно,
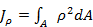(2.2.1)
Осевые и полярный моменты ц всегда положительны и выражаются в см4 или м4.
Отметим интересное свойство: полярный момент инерции Jp равен сумме осевых моментов инерции Jx и Jy, относительно любой пары взаимно перпендикулярных осей х и у, проходящих через полюс 0. Действительно, как видно из рисунка, ρ2= х2 + у2, и =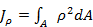 
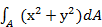
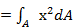
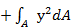= Jx + Jy , следовательно:
Jp = Jx + Jy (2.2.6)
Если оси х и у повернуть относительно полюса О некоторый угол α (рис. 2.2.3), то ρ2=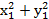 
и, следовательно Jp = Jx1 + Jy1, т. е. при любом повороте осей относительно моментов инерции остается постоянной: Jx + Jy= Jx1 + Jy1= Jp=const.
Центральным моментом инерции сечения относительно осей координат (например, осей х и у) называется сумма произведений элементарных площадей dА на их расстояния до этих осей, которая распространяется на всю площадь сечения А.
Таким образом:
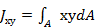(2.2.7)
Центробежный момент инерции Jxу выражается в см4 или м4 и может быть положительным, отрицательным и равным нулю в зависимости от положения сечения относительно осей координат.
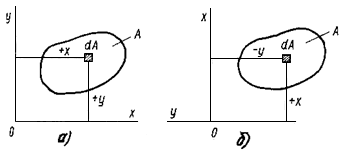
Рисунок 2.2.4
Если сечение занимает положение относительно осей х н у, как показано на рис. 2.2.4, а, то в этом случае Jxу>0, так как координаты х и у положительны. Повернем оси координат на 90° против хода часовой стрелки (рис. 2.2.4, б) Теперь Jxу <0, так как х>0, а у<0. Отсюда следует, что при повороте осей на некоторый угол <90° центробежный момент может быть равен нулю Jxу = 0.
Для некоторых сечений можно сразу указать оси, относительно которых Jxу = 0. Центробежные моменты полусечений симметричных тел, расположенные по разные стороны от оси симметрии у, равны между собой, но отличаются знаками. Следовательно, Jxу = 0.
Пример 2.2.1 Определить моменты инерции относительно центральных осей х н у (рис.2.2.5)
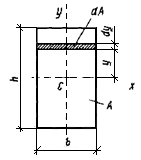
Рисунок 2.2.5
Решение. Разобьем площадь прямоугольника на элементарные прямоугольники с размерами b (ширина) и dy (высота). Тогда площадь такого прямоугольника (на рис 2.2.5 она заштрихована) равна dA=bdy. Подставляя значение dA в формулу (2.2.4) и интегрируя получим:
= 
= 
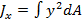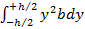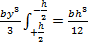
По аналогии запишем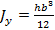 
Центробежный момент инерции Jxу = 0, так как оси х и у являются осями симметрии.