Кривая второго порядка – гипербола. Основные характеристики
Гиперболой называется множество точек плоскости разность расстояний от каждой с которых до двух данных точек 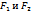 называемых фокусами есть величина постоянная меньшая расстояния между фокусами.
называемых фокусами есть величина постоянная меньшая расстояния между фокусами.
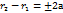 2a<2c
2a<2c
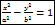 каноническое уравнение гиперболы
каноническое уравнение гиперболы
а- действительная полуось
в – мнимая полуось
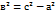
Асимптотами гиперболы называются прямые имеющие уравнение 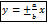 они же диагонали прямоугольника гиперболы.
они же диагонали прямоугольника гиперболы.
Асимптотой кривой называется прямая расстояние до которой от точки лежащей на кривой стремится к 0 при неограниченном удалении этой точки от начала координат.
Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной оси.
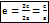 Эксцентриситет
Эксцентриситет
 фокальные радиусы гиперболы
фокальные радиусы гиперболы
Кривая второго порядка – парабола. Основные характеристики
Параболой называется множество точек плоскости в каждой из которых находится на одинаковом расстоянии от данной точки (фокуса) и данной прямой (директрисой).
Начало координат делит пополам отрезок от директрисы до фокуса и этот отрезок (половина) р- параметр параболы.
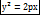 каноническое уравнение параболы
каноническое уравнение параболы
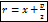 фокальный радиус
фокальный радиус
Точка пересечения параболы с осью симметрии называется вершиной параболы.
Уравнение плоскости. Расстояние от точки к плоскости
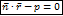 нормальное уравнение плоскости в векторной форме
нормальное уравнение плоскости в векторной форме
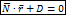 общее уравнение плоскости в векторном виде
общее уравнение плоскости в векторном виде
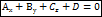 общее уравнение плоскости в координатной форме
общее уравнение плоскости в координатной форме
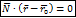 уравнение связки плоскостей в векторной форме
уравнение связки плоскостей в векторной форме
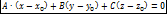
Уравнение связки плоскостей в координатной форме
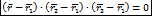 уравнение плоскости проходящей через 3 точки в векторной форме
уравнение плоскости проходящей через 3 точки в векторной форме
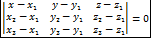 уравнение плоскости проходящей через 3 точки в координатной форме
уравнение плоскости проходящей через 3 точки в координатной форме
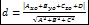 расстояние от точки к плоскости
расстояние от точки к плоскости
Угол между двумя плоскостями. Условия их параллельности и перпендикулярности
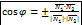 угол между плоскостями в векторной форме
угол между плоскостями в векторной форме
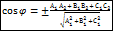 угол между плоскостями в координатной форме
угол между плоскостями в координатной форме
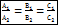 условие параллельности плоскостей
условие параллельности плоскостей
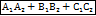 условие перпендикулярности плоскостей
условие перпендикулярности плоскостей
Уравнение прямой в пространстве. Переход от общего уравнения прямой к каноническому
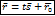 параметрическое уравнение прямой в векторной форме, где t – параметр
параметрическое уравнение прямой в векторной форме, где t – параметр
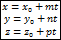 параметрическое уравнение прямой в координатной форме
параметрическое уравнение прямой в координатной форме
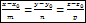 каноническое уравнение прямой
каноническое уравнение прямой
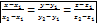 уравнение прямой проходящей через две точки
уравнение прямой проходящей через две точки
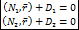 общее уравнение прямой в векторной форме
общее уравнение прямой в векторной форме
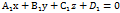
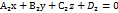 общее уравнение прямой в координатной форме
общее уравнение прямой в координатной форме
При переходе от общего уравнения к каноническому виду надо найти какую-либо точку принадлежащую прямой и вместо коэффициентов m и nподставить пропорциональные им числа.
