Линейные операции над векторами в координатах
Пусть заданы векторы в прямоугольной системе координат
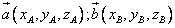 тогда линейные операции над ними в координатах имеют вид:
тогда линейные операции над ними в координатах имеют вид: 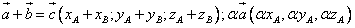
Скалярное произведение векторов и его свойства. Скалярное произведение векторов в координатах.
Скалярным произведением векторов 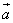 и
и 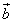 называется число, равное произведению длин этих сторон на косинус угла между ними
называется число, равное произведению длин этих сторон на косинус угла между ними 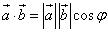 . Свойства:
. Свойства: 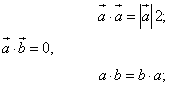 .
.
Если вектора заданы в системе координат, то находим ск пр по формуле: 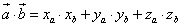 .
.
Приложение скалярного произведения векторов.
С помощью ск пр можно найти: 1)квадрат вектора; 2)угол между векторами; 3)проекцию вектора на вектор; 4)работу силы на перемещение.
Векторное произведение векторов. Свойства векторного произведения векторов.
Упорядоченная тройка некомплинарных векторов а,в,с с общим началом в точке О – называется правой тройкой векторов, если при наблюдении происходит поворот против часовой стрелки, то тройка левая. Векторное произв векторов а на в – наз вектор с, кот удовлетвор след условиям: 1)векторы а,в,с образуют правую тройку; 2)вектор с перпендикулярен а и в; 3) 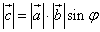 , где фи угол между векторами а и в. Векторное произв обозначается с=ахв или [а;в]. Свойства:1)аха=0, 2)ахв=-вха, 3)ахв=0(параллельны), 4)(альфа*а)хв=альфа*(ахв).
, где фи угол между векторами а и в. Векторное произв обозначается с=ахв или [а;в]. Свойства:1)аха=0, 2)ахв=-вха, 3)ахв=0(параллельны), 4)(альфа*а)хв=альфа*(ахв).
Векторное произведение векторов в координатах.
Если заданы векторы 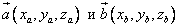 в декартовой прямоугольной системе координат с единичными векторами
в декартовой прямоугольной системе координат с единичными векторами 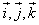 , то
, то 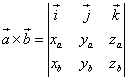 .
.
Приложение векторного произведения векторов.
1)Sпараллелограмма=[axb], 2) Sтреугольника=1/2[axb], 3)опр численности момента силы относительно плеча l в точку О [M]=[Fxl], 4)установление коллониальности векторов ахв=0, а параллельна в или xa/xb=ya/yb=za/zb.
Смешанное произведение векторов. Свойства.
Смешанным произведением векторов а,в,с называется число, равное скалярному произведению вектора а на вектор, равный векторному произведению векторов в,с: а*(вхс). Обозначается 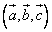 . Смешанное произведение
. Смешанное произведение 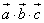 по модулю равно объему параллелепипеда, построенного на векторах
по модулю равно объему параллелепипеда, построенного на векторах 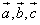 .
.
Свойства смешанного произведения: 1)Смешанное произведение равно нулю, если: а) хоть один из векторов равен нулю; б) два из векторов коллинеарны; в) векторы компланарны; 2) 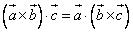 ; 3)
; 3) 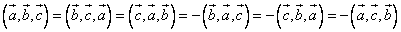 ; 4)
; 4)  .
.
Выражение смешанного произведения векторов через координаты.
Если 3 вектора заданы своими координатами, то смешенное пр находится по формуле (Если 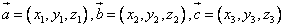 , то
, то 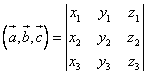 ).
).
Приложение смешанного произведения векторов.
1)3 вектора комплинарны(лежат в одной плоскости) если их вмешанное произведение =0; 2)Объем треугольной пирамиды, образованной векторами 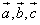 , равен
, равен 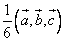 ; 3) объем параллепипеда постоенного на векторох а,в,с равен V=[(а;в;с)].
; 3) объем параллепипеда постоенного на векторох а,в,с равен V=[(а;в;с)].
