Скалярное произведение
Функцию 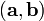 (в другом обозначении
(в другом обозначении 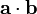 ) ,ставящию любым двум векторам
) ,ставящию любым двум векторам 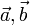 в соответствие число и удовлетворяющию следующим аксиомам:
в соответствие число и удовлетворяющию следующим аксиомам:
- Линейность по первому аргументу:
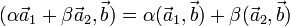 , где α,β - произвольные числа
, где α,β - произвольные числа - Эрмитова симметричность:
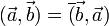 (в случае если вектора определенны над полем действительных чисел, то
(в случае если вектора определенны над полем действительных чисел, то 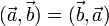 )
) - Положительная определённость:
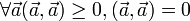 тогда и только тогда, когда
тогда и только тогда, когда 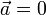
Называется скалярным произведением.
Угол ϕ между векторами 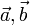 определяется, как
определяется, как 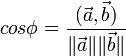
Иногда, когда не известны кооринаты векора, для нахождения скалярного произведения удобнее использовать эту формулу.
Геометрически скалярное произведение есть произведение длины одного из сомножителей на ортогональную проекцию другого на направление первого (или наоборот). Скалярное произведение какого-то вектора 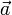 с единичным вектором есть ортогональная проекция вектора
с единичным вектором есть ортогональная проекция вектора 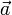 на направление единичного вектора.
на направление единичного вектора.
Векторное произведение
Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям:
- длина вектора c равна произведению длин векторов a и b на синус угла φ между ними
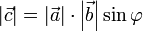
- вектор c ортогонален каждому из векторов a и b
- вектор c направлен так, что тройка векторов abc является правой.
Обозначение: 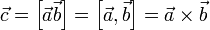
Геометрически векторное произведение 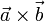 есть ориентированная площадь параллелограмма, построенного на векторах
есть ориентированная площадь параллелограмма, построенного на векторах 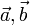 , представленная псевдовектором, ортогональным этому параллелограмму.
, представленная псевдовектором, ортогональным этому параллелограмму.
Свойства векторного произведения:
- При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е
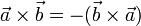
- Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть
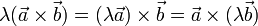
- Векторное произведение обладает распределительным свойством:
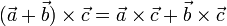
] Смешанное произведение
Сме́шанное произведе́ние 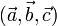 векторов
векторов 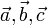 — скалярное произведение вектора
— скалярное произведение вектора 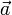 на векторное произведение векторов
на векторное произведение векторов 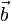 и
и 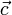 :
:
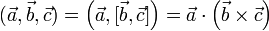
(равенство записано для разных обозначений скалярного и векторного произведения).
Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрически смешанное произведение 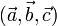 есть (ориентированный) объём параллелепипеда, построенного на векторах
есть (ориентированный) объём параллелепипеда, построенного на векторах 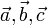 .
.
Вычетание векторов
Чтобы из вектора а вычесть вектор b надо к вектору а прибавить вектор, противоположный вектору b. Полученный в результате этой операции вектор си будет являться разностью векторов аи b. Таким образом,
с = а − b = а + (− b).
Рисунок 5 иллюстрирует операциювычитания векторов.

