Скалярное произведение
Разложение вектора по ортам координатных осей.
Модуль вектора. Направляющие косинусы
Рассмотрим в пространстве прямоугольную систему координат Охуг. Выделим на координатных осях Ох, Оy и Оz единичные векторы (орты), обозначаемые 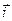 ,
, 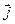 ,
, 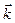 соответственно (рис. 2.5).
соответственно (рис. 2.5).
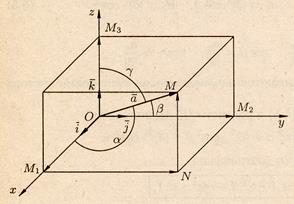
Рис. 2.5.
Выберем произвольный вектор 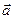 пространства и совместим его начало с началом координат:
пространства и совместим его начало с началом координат: 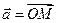 .
.
Проведем через конец вектора 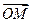 плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через
плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через 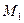 ,
, 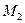 ,
, 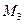 . Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор
. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор 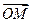 .
.
Тогда, используя определение суммы векторов, последовательно получаем.
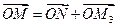 ,
, 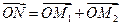 ,
, 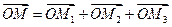 и, следовательно
и, следовательно
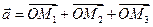 . . | (2.2) |
Учитывая, что вектор равен произведению его модуля на орт, получаем
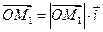 , , 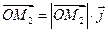 , , 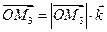 . . | (2.3) |
Обозначим
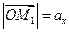 ,
, 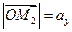 ,
, 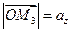
тогда из равенств (2.2) и (2.3) следует, что
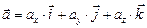 | (2.4) |
Представление вектора 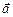 в виде (2.4) называется разложением вектора
в виде (2.4) называется разложением вектора 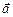 по базису
по базису 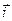 ,
, 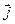 ,
, 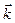 .
.
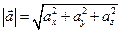 | (2.5) |
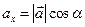 , , 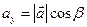 , , 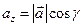 | (2.6) |
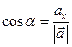 , , 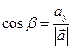 , , 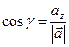 | (2.7) |
Координаты вектора 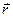 в базисе
в базисе 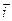 ,
, 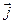 ,
, 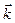 обозначим x, у, z. Таким образом, координаты точки М (x, у, z) – это также и координаты
обозначим x, у, z. Таким образом, координаты точки М (x, у, z) – это также и координаты 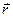 , поэтому
, поэтому 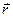 = х
= х 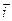 + y
+ y 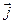 + z
+ z 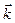 .
.
Направленные прямые, проходящие через точку О и сонаправленные с базисными векторами 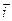 ,
, 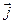 ,
, 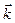 называются осями координат соответственно Ох, Оy и Оz. Координаты вектора
называются осями координат соответственно Ох, Оy и Оz. Координаты вектора 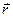 ( x, у, z ) – это проекции вектора
( x, у, z ) – это проекции вектора 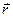 на оси Ох, Оy и Оz.
на оси Ох, Оy и Оz.
Рассмотрим две точки А(x1 , y1, z1) и В (x2, y2, z2), радиус-векторы которых 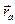 и
и 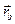 . Так как
. Так как 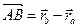 = (x2– x1, y2– y1, z2– z1), то приходим к следующему выводу: чтобы найти координаты вектора
= (x2– x1, y2– y1, z2– z1), то приходим к следующему выводу: чтобы найти координаты вектора 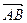 , нужно из координат его конца вычесть соответствующие координаты его начала.
, нужно из координат его конца вычесть соответствующие координаты его начала.
Пример 2.1
Найти вектор 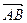 , если А(5;8;–1), В(1;3;2).
, если А(5;8;–1), В(1;3;2).
Решение
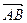 =(1–5; 3–8; 2–(–1)) Þ
=(1–5; 3–8; 2–(–1)) Þ 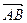 =(– 4; –5; 3) или
=(– 4; –5; 3) или 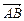 =
= 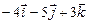 .
.
Для случая плоскости декартова система координат определяется началом координат О и двумя базисными векторами 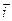 ,
, 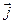 .
.
Соответственно применяются записи для точки плоскости М (х, у) и вектора в плоскости 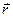 (x, у).
(x, у).
Пример 2.2
Найти орт 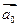 вектора
вектора 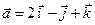 .
.
Решение
Из решения получаем 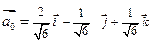 .
.
Векторы 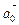 и
и 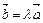 коллинеарны (параллельны). Из равенства векторов
коллинеарны (параллельны). Из равенства векторов 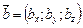 и
и 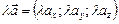 следует равенство соответствующих координат bx=lax, by=lay, bz=laz. Из этих трех равенств получается условие коллинеарности векторов
следует равенство соответствующих координат bx=lax, by=lay, bz=laz. Из этих трех равенств получается условие коллинеарности векторов 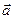 и
и 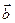 :
:
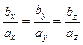 | (2.8) |
Пример 2.3
При каких значениях a и b векторы 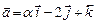 и
и 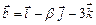 коллинеарны?
коллинеарны?
Решение
Из коллинеарности векторов 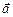 и
и 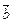 следует пропорциональность их координат
следует пропорциональность их координат
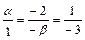 Þ a =
Þ a = 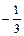 ,
, 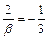 Þ b = – 6.
Þ b = – 6.
Сумма и разность векторов 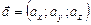 и
и 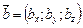 определяется по формулам
определяется по формулам
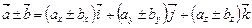 .
.
Сумма векторов 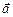 и
и 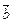 , начала которых совмещены, изображается вектором с тем же началом, совпадающим с диагональю параллелограмма, сторонами которого являются векторы
, начала которых совмещены, изображается вектором с тем же началом, совпадающим с диагональю параллелограмма, сторонами которого являются векторы 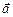 и
и 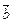 . Разность
. Разность 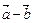 этих векторов изображается вектором, совпадающим со второй диагональю того же параллелограмма, причем начало этого вектора находится в конце вектора
этих векторов изображается вектором, совпадающим со второй диагональю того же параллелограмма, причем начало этого вектора находится в конце вектора 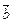 , а конец – в конце вектора
, а конец – в конце вектора 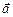 (см. рис.1.2).
(см. рис.1.2).
Скалярное произведение
Определение. Скалярным произведением векторов 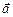 и
и 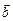 называется число, равное произведение модулей этих векторов на косинус угла между ними. Обозначается скалярное произведение так:
называется число, равное произведение модулей этих векторов на косинус угла между ними. Обозначается скалярное произведение так: 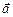 ×
× 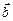 или
или 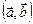 . Таким образом, по определению,
. Таким образом, по определению,
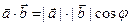 , , | (2.9) |
где j – угол между векторами 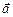 и
и 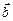 .
.
Свойства.Рассмотрим некоторые важные свойства скалярного произведения:
1. 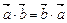 .
.
2. 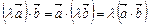 .
.
3. 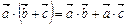 .
.
4. 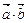 =0 тогда и только тогда, когда сомножители ортогональны (один из них может быть нулевым вектором)
=0 тогда и только тогда, когда сомножители ортогональны (один из них может быть нулевым вектором)
5. 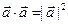 .
.
6. 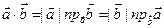 .
.
Свойства 1), 4), 5) следуют непосредственно из определения скалярного произведения.
Докажем свойство 6. По определению, 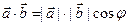 . Но
. Но 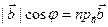 , откуда
, откуда 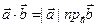 . Совершенно аналогично доказывается, что
. Совершенно аналогично доказывается, что 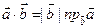 .
.
Свойства 2) и 3) доказываются с помощью свойства 6) и свойств проекций. Действительно, 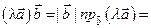
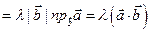 ;
;
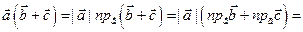
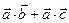 .
.
Величина 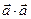 называется скалярным квадратом вектора
называется скалярным квадратом вектора 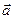 и обозначается символом
и обозначается символом 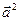 . Из свойства 5) следует, что скалярный квадрат вектора равен квадрату его модуля
. Из свойства 5) следует, что скалярный квадрат вектора равен квадрату его модуля 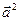 =
= 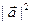 .
.
Вычисление.Выведем формулу вычисления скалярного произведения векторов, заданных координатами.
Рассмотрим базис 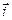 ,
, 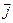 ,
, 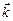 . Скалярные произведения одноименных векторов базиса равны единице:
. Скалярные произведения одноименных векторов базиса равны единице: 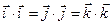 =1, так как это скалярные квадраты единичных векторов. Скалярные произведения различных векторов базиса равны нулю:
=1, так как это скалярные квадраты единичных векторов. Скалярные произведения различных векторов базиса равны нулю:
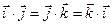 = 0, так как это скалярные произведения
= 0, так как это скалярные произведения
ортогональных векторов.
Пусть 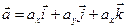 ,
, 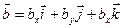 . Используя свойства 2 и 3 скалярного произведения, последовательно получаем
. Используя свойства 2 и 3 скалярного произведения, последовательно получаем
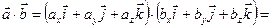
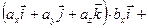
+ 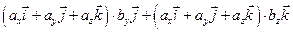 =
= 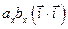 +
+
+ 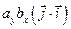 +
+ 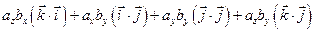 +
+
+ 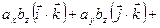
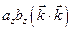 =
= 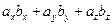 .
.
Таким образом, скалярное произведение векторов равно сумме произведений соответствующих координат
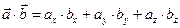 . . | (2.10) |
В частности, 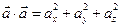 , поэтому, учитывая свойство 5) скалярного произведения, получаем |
, поэтому, учитывая свойство 5) скалярного произведения, получаем | 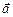 |=
|= 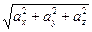 (см. формулу (2.5).
(см. формулу (2.5).
Пример 2.1
Вычислить 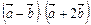 , если |
, если | 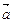 |=3, |
|=3, | 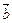 |= 4,
|= 4, 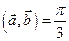 .
.
Решение
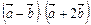 =
= 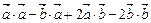 =
= 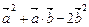 =
= 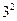 +
+ 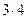 ×
× 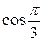 –
– 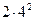 = 9 +
= 9 + 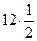 –32 = –17.
–32 = –17.
Пример 2.2
Найти скалярное произведение векторов
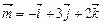 и
и 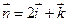 .
.
Решение
По формуле (2.10), получаем 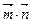 = (–1)× 2 + 3×0 + 2×1 = 0. Отметим, что из равенства нулю скалярного произведения, следует, что векторы
= (–1)× 2 + 3×0 + 2×1 = 0. Отметим, что из равенства нулю скалярного произведения, следует, что векторы 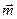 и
и 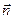 ортогональны.
ортогональны.
Приложения.Рассмотрим некоторые приложения скалярного произведения
1. Вычисление угла между векторами 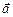 и
и 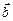 :
:
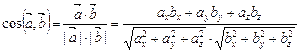 | (2.11) |
Пример 2.3
Найти внутренний угол при вершине С в треугольнике АВС, если A(1;–2; 3), B(–2; –1; 1), C(–3; 4; 5).
Решение
Искомый угол a это угол между векторами 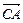 =(4; –6;–2)и
=(4; –6;–2)и 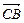 = (1; –5;–4); тогда
= (1; –5;–4); тогда
сos a = 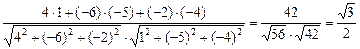 Þ
Þ
Þ a = p/6.
2. Вычисление проекции вектора 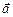 на вектор
на вектор 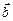 :
:
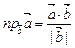 | (2.12) |
Пример 2.4
Найти проекцию вектора 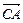 на вектор
на вектор 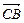 из примера 2.3.
из примера 2.3.
Решение
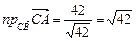 .
.
3. Условие ортогональности векторов 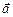 и
и 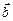 :
:
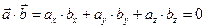 . . | (2.13) |
Пример 2.5
При каком значении 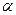 вектор
вектор 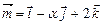 ортогонален вектору
ортогонален вектору 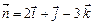 ?
?
Решение
Запишем условие ортогональности (2.13) для векторов 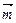 и
и 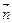 : 1×2 + (–a)×1 + + 2×(–3) = 0. Из этого уравнения получаем значение
: 1×2 + (–a)×1 + + 2×(–3) = 0. Из этого уравнения получаем значение 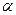 = – 4.
= – 4.
4. Вычисление работы 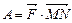 при прямолинейном перемещении точки из положения М в положение N под действием силы
при прямолинейном перемещении точки из положения М в положение N под действием силы 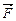 .
.
Пример 2.6
Вычислить работу, которую производит сила 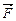 =(3; –5; –6) на отрезке пути AB, если A(1; –3; –2), B(3; –7; –1).
=(3; –5; –6) на отрезке пути AB, если A(1; –3; –2), B(3; –7; –1).
Решение
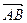 = (2; – 4; 1); А =
= (2; – 4; 1); А = 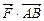 = 3×2 + (–5)×(–4) + (–6)×1 = 20 (ед. работы).
= 3×2 + (–5)×(–4) + (–6)×1 = 20 (ед. работы).
