Выражение скалярного произведения через координаты

Линейные операции над векторами.

1. Суммой любого конечного числа векторов есть отрезок соеденяющий начало первого с концом последнего, при условии что в-ра расположенны так что конец предидущего совпадает с началом последующего .

1. Правило паралелограма: суммой двух ненулевых векторов выходящей из одной точки есть третий вектор являющийся диагональю паралелограмма построенного на 2х данных векторах как на сторонах.

2. Правило Паралелепипеда: суммой 3х ненулевых векторов имеющих общее начало есть 4й вектор выходящей из того же начала и совпадающий с диагональю паралелепипеда построенного на векторах как на рёбрах.

2. Умножение векторов на скаляр. Произведением вектора А на число k есть вектор у которого:
1. Длина совпадёт с направлением вектора А если k>0 и противоположно если k <0.

Свойства:

1. (k1+ k2)*А=А* k1+А* k2.

2. k 1* k2*А= k1*( k2*А)= k2*( k1*А)

3. K*(А+В)= k*А+ k*А

Вычитание векторов

1. Разница 2х ненулевых векторов А и В выходящих из одного начала есть третий вектор С соединяющий конец вычитаемого с концом уменьшаемого.

СВОЙСТВА.

1. Любой ненулевой вектор можна выразить через орт.

2. 2 колинеарных вектора всегда можна выразить один через другой.

3. Если вектор R компланарен 2м неколинеарным векторам А и В, то: R=m*a+n*b. R – разложен по А и В. Любой ненулевой вектор можна еденичным способом разложить по 2м некомпланарным векторам в-ам.

5.Разложение вектора по ортам координатных осей.

1. Выделим на осях орты I j k, поместим в это пространство А, совместив начало вектора с началом координат. Найдём проэкции этого вектора на оси координат – для этого проведём через точку М или плоскости перпендикулярных осям ординаты. Обозначим точки пересечения М1 М2 М3 соответственно. Рассмотрим ОМ1, ОМ2, ОМ3.

ОМ1=|OM1|*i=a_x*i

OM2=|OM2|*j=a_y*j

OM3=|OM3|*k=a_z*k

Найдём сумму ОМ1+ОМ2+ОМ3=А.

А= a_x*i+a_y*j+a_z*k.

a_y a_x a_z – проекции вектора на оси соответственно.

Следствия:

1. Координаты орт. А совпадают с его направляющим косинусом. Направляющие косинусы: cosα= a_x/|A|, cosβ= a_y/|A|, cosγ= a_z/|A|

2. Для любоо вектора справедливо равенство cos² α+ cos² β+ cos² γ=1.

6. Действия над векторами:

рассматриваются вектора и в пространстве.

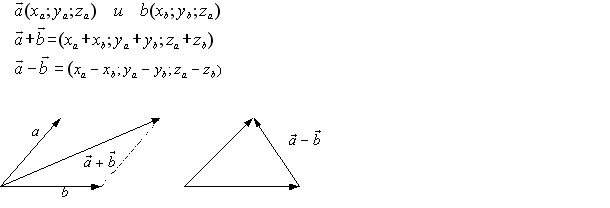
Скалярное произведение векторов и его свойства

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними.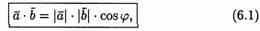

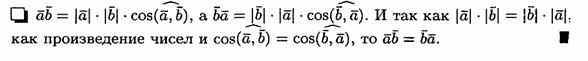
Если векторы а и b(ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a ^b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а¹ 0 ¹b, то а ^ b

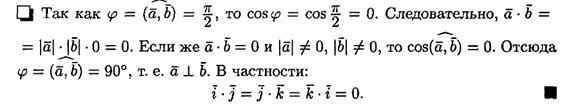
Выражение скалярного произведения через координаты

Пусть заданы два вектора

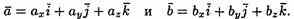
Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:

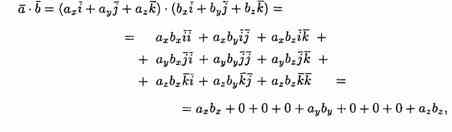
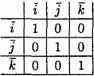
т.е

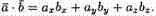
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.