Понятие линейной зависимости векторов

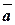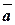Определение 9.Пусть дана система векторов ₁, ₂, …, 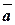_n и совокупность 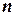вещественных чисел 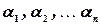. Тогда выражение вида 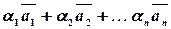называется линейной комбинацией векторов, а числа 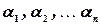называются коэффициентами линейной комбинации. Если некоторый вектор 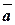представлен как линейная комбинация векторов 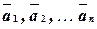, т.е. в виде: 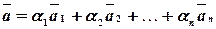, то говорят, что вектор 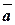разложен по этим векторам.

Определение 10.Векторы 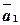, , 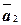…, 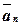называются линейно зависимыми, если существует набор коэффициентов 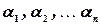, одновременно не равных нулю 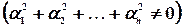и таких, что

.

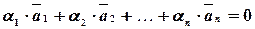Определение 11.Векторы 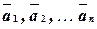называются линейно независимыми, если равенство нулю линейной комбинации этих векторов возможно лишь при всех коэффициентах одновременно равных нулю.

Определение 12. Базисом на прямой называется любой ненулевой вектор на этой прямой.

Определение 13. Базисом на плоскости называются два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.

Определение 14.Базисом в пространстве 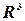называются три линейно независимые вектора в этом пространстве, взятые в определенном порядке.

Теорема 1 (о разложении вектора по базису в пространстве R³)

Пусть даны три некомпланарные вектора: 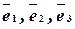. Любой вектор 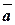раскладывается по ним. Такое разложение единственно. Существует набор чисел 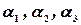такой, что:

_.

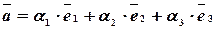Свойства линейно зависимой и линейно независимой системы векторов:

1) Если хотя бы один из 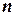векторов есть нуль вектор, то все 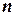векторов линейно зависимы.

2) Если среди 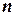векторов какие-либо 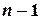векторов линейно зависимы, то все 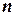векторов линейно зависимы.

3) Для того чтобы два ненулевых вектора были линейно зависимы необходимо и достаточно, чтобы они были коллинеарными.

4) Пусть 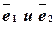- два неколлинеарных вектора плоскости. Любой компланарный с ними вектор 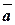раскладывается по ним: 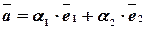. Такое разложение единственно.

5) Три компланарных вектора линейно зависимы. Три некомпланарных вектора пространства линейно независимы.

6) Любые четыре вектора пространства 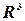линейно зависимы.

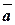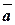7) Система векторов ₁, ₂, …, 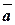_n линейно зависима тогда и только тогда, когда один из них раскладывается в линейную комбинацию остальных.

Понятие о проекциях.

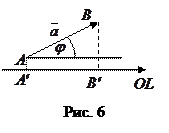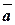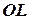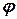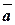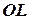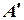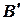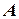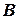Пусть дан вектор и ось , - угол между вектором и положительным направлением оси . и - основания перпендикуляров, опущенных из точек и соответственно (см. рис. 6).

Определение 15.Проекцией вектора на ось называется длина отрезка оси 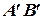, взятая со знаком плюс, если вектор 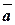образует острый угол с направлением оси, и со знаком минус в противоположном случае.

Теорема 2.Проекция вектора 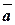на ось 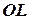равна произведению длины вектора на косинус угла между вектором и осью: .

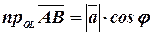Следствие. При умножении вектора 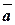на некоторое число 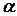его проекция умножается на это же число: .

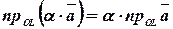Теорема 3 (о проекции суммы).Проекция суммы некоторого числа векторов на ось 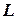равна сумме проекций слагаемых векторов: , .

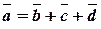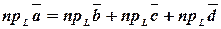Декартова система координат.

Ортонормированный базис образуют взаимно перпендикулярные векторы 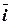, , 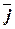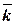единичной длины, т.е.

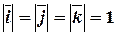и .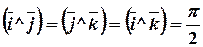

Точка 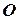- начало координат 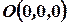. Прямые, проходящие через начало координат в направлении векторов 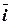, , 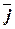, 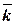называются осями координат. Векторы 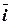, , 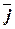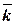соответствуют положительному направлению осей координат: 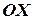, , 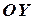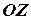- оси абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями 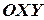, , 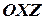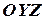(см. рис. 7).

Определение 16. Прямоугольной системой координат называется совокупность точки ( 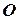) и ортонормированного базиса.

Определение 17. Радиус-вектором произвольной точки 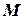по отношению к точке 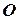, называется вектор 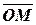. Точке 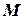можно сопоставить упорядоченную тройку чисел ( 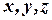) - компоненты ее радиус-вектора: 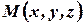и 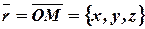(см. рис. 8).

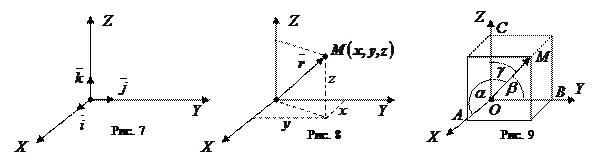Определение 18.Компоненты радиус-вектора точки 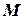по отношению к началу координат называют координатами точки 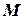в рассматриваемой системе координат.

Координаты вектора совпадают с проекцией вектора на соответствующие оси координат (рис.8):

, , , ,

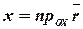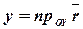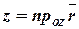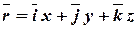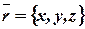
Согласно рис. 9 имеем: , , , ,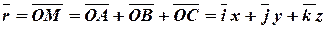

.

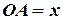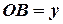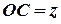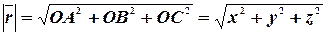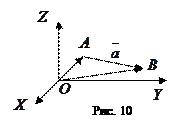Пусть вектор 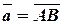задан координатами крайних точек, 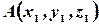и 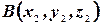(рис. 10).

Тогда

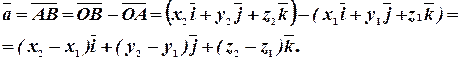
Следовательно, чтобы определить координаты вектора по координатам крайних точек, надо из координат конца вычесть соответствующие координаты начала: .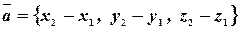

Определение 19. Пусть 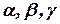- углы между вектором 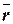и соответственно ортами 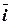, , 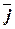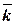(рис. 9), тогда направляющие косинусывектора 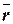определяются по правилу:

,

,

,

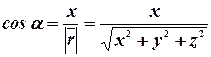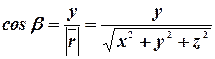Следовательно, сумма квадратов направляющих косинусов равна : .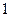

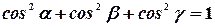Пример 1. Даны точки , , , .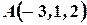

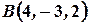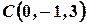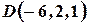Найти координаты и длину вектора .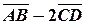

Решение. Найдем координаты векторов 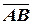и :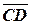

, ,

, .

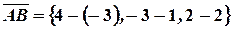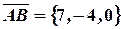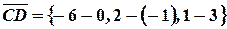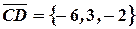По правилам действий с векторами, получим:

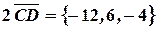и }.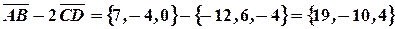

Теперь находим длину искомого вектора:

= = .

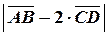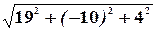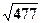Пример 2. Даны точки , .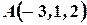

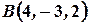Найти направляющие косинусы вектора .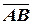

Решение. Так как 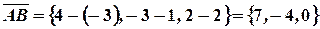, то 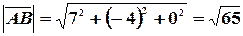и направляющие косинусы находятся согласно формулам:

, , .
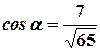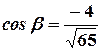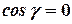