Умножение вектора на число

Свойства

Ортогональность

Векторы являются ортогональными тогда и только тогда, когда их скалярное произведение равно нулю.

Часто вместо этого термина употребляют термин «перпендикулярность», однако следует учитывать, что нулевой вектор ортогонален любому вектору, но понятие перпендикулярности для него не определено, поскольку не определён угол между нулевым и другим вектором.

Пример:
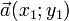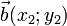Даны два вектора и , с координатами в ортонормированном базисе. Эти векторы будут ортогональными, если выражение x₁x₂ + y₁y₂ = 0.

Коллинеарность

Два не нулевых вектора 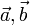называются коллиниарными, если 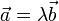, где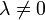

Векторы являются коллинеарными тогда и только тогда, когда их векторное произведение равно нулю.

Часто вместо этого термина употребляют термин «параллельность», однако следует учитывать, что нулевой вектор коллинеарен любому вектору, но понятие параллельности для него не определено, поскольку не определён угол между нулевым и другим вектором.

Сложение геометрических векторов

Два вектора u, v и вектор их суммы

Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.

Правило треугольника. Для сложения двух векторов 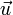и 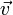по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Правило параллелограмма. Для сложения двух векторов 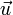и 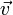по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

А модуль (длину) вектора суммы 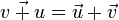определяют по теореме косинусов 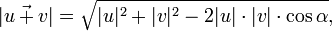где 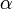— угол между векторами, когда начало одного совпадает с концом другого. Так же используется формула 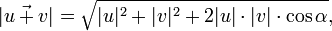теперь 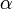— угол между векторами выходящими из одной точки.

Умножение вектора на число

Произведением вектора 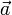и числа λ называется вектор, обозначаемы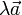й (или 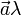), модуль которого равен , а направление совпадает с направлением вектора 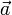, если 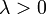, и противоположно ему, если 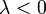. Если же 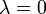, или вектор 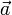нулевой, тогда и только тогда произведение 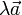— нулевой вектор.

• Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе, .

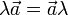Из определения произведения вектора на число легко вывести следующие свойства: