Основы теории нечетких множеств и нечеткой логики

Одним из методов изучения множеств без уточнения их границ является теория нечетких множеств, которая была предложена в 1965 г. профессором Калифорнийского университета Лотфи Заде. Первоначально она разрабатывалась как средство моделирования неопределенности естественного языка. Однако впоследствии круг задач, решаемых с использованием аппарата нечетких множеств, значительно расширился и сейчас включает в себя такие области, как анализ данных, распознавание, исследование операций, моделирование сложных систем, поддержка принятия решений и т. д. [4, 5].

Нередко при определении и описании характеристик объектов оперируют не только количественными, но и качественными значениями. В частности, рост человека можно количественно измерить в сантиметрах, а можно описать, используя качественные значения: карликовый, низкий, средний, высокий или гигантский. Интерпретация качественных значений носит субъективный характер, т.е. они могут по-разному трактоваться разными людьми (субъектами). В силу нечеткости (размытости) качественных значений, при необходимости перехода от них к количественным величинам возникают определенные трудности.

В системах, построенных на базе нечетких множеств, используются правила вида «ЕСЛИ А ТО В» (А ® В), в которых как в А (условие, предпосылку), так и в В (результат, гипотезу) могут входить качественные значения. Например, «ЕСЛИ Рост = "высокий" ТО Вид_спорта = "баскетбол"».

Переменная, значение которой определяется набором качественных значений некоторого свойства, в теории нечетких множеств называются лингвистической. В приведенном примере правила используются две лингвистические переменные: Рост и Вид_спорта.

Каждое значение лингвистической переменной определяется через так называемое нечеткое множество. Нечеткое множество определяется через некоторую базовую шкалу X и функцию принадлежности (характеристическую функцию) m(х), где х Î Х. При этом, если в классическом канторовском множестве элемент либо принадлежит множеству (m(х) = 1), либо не принадлежит (m(х) = 0), то в теории нечетких множеств m(х) может принимать любое значение в интервале [0, 1]. Над нечеткими множествами можно выполнять стандартные операции: дополнение (отрицание), объединение, пересечение, разность и т. д. (рис. 33).

Для нечетких множеств существует также ряд специальных операций: сложение, умножение, концентрирование, расширение и т. д.

При задании лингвистической переменной ее значения, т. е. нечеткие множества, должны удовлетворять определенным требованиям (рис. 34).

1. Упорядоченность. Нечеткие множества должны быть упорядочены (располагаться по базовой шкале) в соответствии с порядком задания качественных значений для лингвистической переменной.

2. Ограниченность. Область определения лингвистической переменной должна быть четко обозначена (определены минимальные и максимальные значения лингвистической переменной на базовой шкале). На границах универсального множества, где определена лингвистическая переменная, значения функций принадлежности ее минимального и максимального нечеткого множества должны быть единичными. На рисунке Т₁ имеет неправильную функцию принадлежности, а Т₆ – правильную.

3. Согласованность. Должно соблюдаться естественное разграничение понятий (значений лингвистической переменной), когда одна и та же точка универсального множества не может одновременно принадлежать с m(х) = 1 двум и более нечетким множествам (требование нарушается парой Т₂ – Т₃).

4. Полнота. Каждое значение из области определения лингвистической переменной должно описываться хотя бы одним нечетким множеством (требование нарушается между парой T₃ – Т₄).

5. Нормальность. Каждое понятие в лингвистической переменной должно иметь хотя бы один эталонный или типичный объект, т. е. в какой-либо точке функция принадлежности нечеткого множества должна быть единичной (требование нарушается T₅).

m(х)

0 20 40 60 80 100 110 120 140 160 X

Нечеткое множество «низкий рост» m_н(х)

m(х)

0 20 40 60 80 100 110 120 140 160 X

Нечеткое множество «высокий рост» m_в(х)

m(х)

0 20 40 60 80 100 110 120 140 160 X

Д = Н : Дополнение нечеткого множества «низкий рост»

m_д(х) = 1 – m_н(х)

m(х)

0 20 40 60 80 100 110 120 140 160 X

Н È В : Объединение нечетких множеств «низкий рост» и «высокий рост»

m_нв(х) = mах(m_н(х), m_в(х))

m(х)

0 20 40 60 80 100 110 120 140 160 X

Н Ç В : Пересечение нечетких множеств «низкий рост» и «высокий рост»

m_нв(х) = min(m_н(х), m_в(х))

Рис. 33. Операции над нечеткими множествами

m(х) Т₁ Т₂ Т₃ Т₄ Т₅ Т₆

X

Рис. 34. Пример задания нечетких множеств для линг­вис­тической переменной с нарушением требований

Требования 2–4 можно заменить одним универсальным – сумма функций принадлежности m(х) по всем нечетким множествам в каждой точке области определения переменной должна равняться 1.

При обработке правил с лингвистическими переменными (нечетких правил) для вычисления истинности гипотезы применяются правила нечеткой логики. Нечеткая логика – разновидность непрерывной логики, в которой предпосылки, гипотезы и сами логические формулы могут принимать истинностные значения с некоторой долей вероятности.

Основные положения нечеткой логики:

· истинность предпосылки, гипотезы или формулы лежит в интервале [0, 1];

· если две предпосылки (Е₁ и Е₂) соединены Ù (логическим И), то истинность гипотезы Н рассчитывается по формуле t(Н) = MIN(t(Е₁), t(Е₂));

· если две предпосылки (Е₁ и Е₂) соединены Ú (логическим ИЛИ), то истинность гипотезы Н рассчитывается по формуле t(Н) = MAX(t(Е₁), t(Е₂));

· если правило (П) имеет свою оценку истинности, тогда итоговая истинность гипотезы Н_итог корректируется с учетом истинности правила t(Н_итог) = MIN(t(Н), t(П)).

Процедура обработки нечетких правил состоит из 4 этапов.

Этап 1. Вычисление значений функций принадлежности (истинности) для нечетких множеств лингвистических переменных, входящих в левые части правил.

Этап 2. Модификация нечетких множеств для лингвистической переменной, указанной в правой части правил, в соответствии со значениями функции принадлежности, полученными на первом этапе.

Этап 3. Объединение (суперпозиция) модифицированных множеств.

Этап 4. Скаляризация результата суперпозиции – переход к числовым значениям лингвистических переменных, указанных в правой части. Обычно определяется как центр тяжести суперпозиции соответствующих модифицированных множеств.

4.2. Лабораторная работа № 8. Решение прикладной задачи
с использованием нечетких множеств

Цель работы:освоение аппарата теории нечетких множеств на примере решения прикладной задачи.

Описание задачи и пример ее решения

А. Описание задачи

Вентилятор комнатного кондиционера управляется встроенным программно-аппаратным блоком, работающим на базе нечетких множеств.

Основу программной реализации составляют три экспертных правила, определяющие зависимость скорости вращения вентилятора V от температуры воздуха в помещении t.

1. ЕСЛИ t = «низкая», ТО V = «низкая».

2. ЕСЛИ t = «средняя», ТО V = «средняя».

3. ЕСЛИ t = «высокая», ТО V = «высокая».

Данные правила определяют две лингвистические переменные:

· температура воздуха в помещении t Î {«низкая», «средняя», «высокая»};

· скорость вращения вентилятора V Î {«низкая», «средняя», «высокая»}.

Для каждого качественного значения каждой лингвистической переменной экспертным путем определены нечеткие множества. При этом температура воздуха в комнате может варьироваться от 0 до 60 °С,
а скорость вращения вентилятора – от 0 до 1000 об/мин (рис. 35).

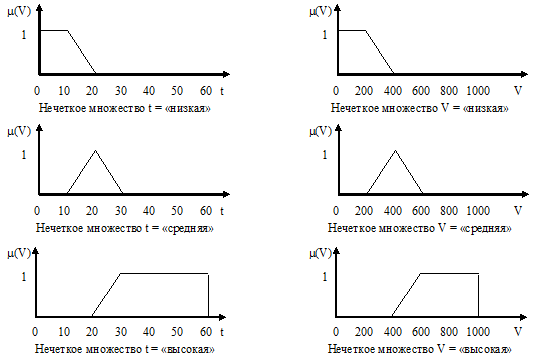
Рис. 35. Нечеткие множества для лингвистических переменных t и V

Предположим, что датчик кондиционера определил температуру воздуха в помещении, равную 22 °C. Процедура определения скорости вращения вентилятора выглядит следующим образом.

Этап 1. В левых частях правил указаны три нечетких множества, заданных на интервале t. Определенные значения функции принадлежности: m_{Tнизкая}(22) = 0, m_{Tсредняя}(22) = 0,8 и m_{Tвысокая}(22) = 0,2.

Этап 2. Полученные значения используются для модификации нечетких множеств правых частей методом «умножения» (рис. 36).

h XK9tu+4/Bcz9/XgO4+MPlukPAAAA//8DAFBLAwQUAAYACAAAACEAC86jsN8AAAAIAQAADwAAAGRy cy9kb3ducmV2LnhtbEyPQUvDQBCF74L/YRnBm90kJTXGbEop6qkItoJ4m2anSWh2NmS3SfrvXU96 HN7He98U69l0YqTBtZYVxIsIBHFldcu1gs/D60MGwnlkjZ1lUnAlB+vy9qbAXNuJP2jc+1qEEnY5 Kmi873MpXdWQQbewPXHITnYw6MM51FIPOIVy08kkilbSYMthocGetg1V5/3FKHibcNos45dxdz5t r9+H9P1rF5NS93fz5hmEp9n/wfCrH9ShDE5He2HtRKcgXT0GUsFTAiLEyyxNQRwDl2QRyLKQ/x8o fwAAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0Nv bnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAALAAAAAAAAAAAAAAAA AC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQAco9GvFwMAAPgMAAAOAAAAAAAAAAAAAAAA AC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQALzqOw3wAAAAgBAAAPAAAAAAAAAAAA AAAAAHEFAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAfQYAAAAA "> 1 * 0,8 =     0 200 400 600 800 1000

0,8 0 200 400 600 800 1000

1 * 0,2 =     0 200 400 600 800 1000

0,2 0 200 400 600 800 1000

Рис. 36. Модификация нечетких множеств

Рис. 37. Объединение модифи­ци­ро­ван­ных нечетких множеств

Этап 3. Объединение (суперпозиция) модифицированных нечетких множеств (рис. 37).

Этап 4. Скалярное значение суперпозиции соответствует координате центра тяжести на базовой шкале. Для ее определения фигуру, указанную на рис. 37, необходимо разбить на элементарные треугольники и прямоугольники (рис. 38), определение центров тяжести которых не составляет труда.

0,8

0,2

F1

F3

F2

0 200 400 600 800 1000

Рис. 38. Разбиение на элементарные фигуры

Геометрически центр тяжести треугольника находится на пересечении медиан, прямоугольника – диагоналей. Математически координаты центра тяжести этих фигур определяются по следующим формулам:

а) треугольника:

; ;

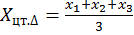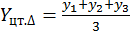б) прямоугольника:

; ,

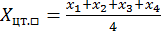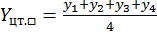где x_i и y_i – координаты i-й вершины треугольника (прямоугольника).

Координаты третьей вершины треугольника F₂ можно определить, исходя из подобия треугольников.

.

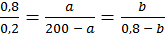Рис. 39. Схема для определения координат третьей вершины треугольника

Из соотношения получаем: а = 160 и b = 0,64. Таким образом, x₃ = 560 и y₃ = 0,16.

Координаты центров тяжести фигур:

; ;

; ;

; .

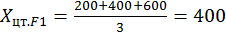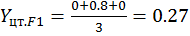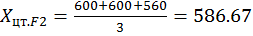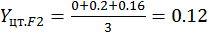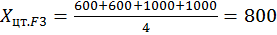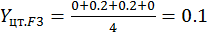Центр тяжести суперпозиции определяется как средневзвешенная величина по формулам:

;

;

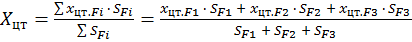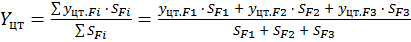где S_Fi – площадь i-й фигуры.

Площади фигур:

;

;

.

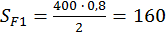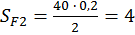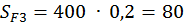Центр тяжести суперпозиции:

;

.

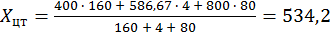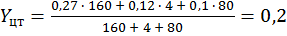Таким образом, скорость вращения вентилятора при t = 22 °C должна быть V = X_цт = 534,2 об/мин.

Задание на выполнение работы

Выполнить расчеты скорости вращения вентилятора V в зависимости от температуры воздуха t для пяти итераций с использованием нечетких множеств.

А. Индивидуальный вариант начальной температуры (температуры для первой итерации):

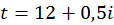, °С,

где 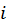– номер варианта.

Б.Для оставшихся итераций температуру принять по формуле

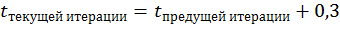, °С.

В. Отчет должен содержать:

· титульный лист;

· номер варианта;

· правила корректировки скорости вращения вентилятора;

· исходные графики (см. рис. 35);

· для каждой итерации:

o значение текущей температуры;

o графики для этой температуры (см. рис. 36);

o расчет площадей и координат X центров тяжести элементарных фигур, входящих в суперпозицию множеств (см. рис. 38);

o расчет координаты X центра тяжести суперпозиции множеств (определенная скорость вращения вентилятора);

· итоговый график изменения скорости вращения вентилятора в зависимости от температуры воздуха в помещении по результатам расчета пяти итераций V(t).

Контрольные вопросы

1. Дайте определения понятий «лингвистическая переменная» и «нечет­кое множество».

2. Перечислите основные операции над нечеткими множествами.

3. Перечислите требования, предъявляемые к заданию нечетких мно­жеств.

4. Опишите процедуру обработки нечетких множеств.

5. В чём заключается отличие нечеткой логики от традиционной?

ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ

Эволюционные вычисления

Эволюционные вычисления являются одним из возможных эвристических подходов к решению оптимизационных задач большой размерности за счет сочетания элементов случайности и детерминированности точно так, как это происходит в живой природе [5]. Информационные системы эволюционных вычислений построены на принципах генетических и эволюционных процессов в природе, когда из набора кандидатов (популяции), получаемого посредством скрещивания и мутаций, по принятому критерию отбираются лучшие, наиболее приспособленные для решения задачи.

Одно из наиболее популярных направлений эволюционных вычислений – генетические алгоритмы, предложенные профессором Мичиганского университета Джоном Холландом в 1975 г. Отличительной особенностью генетических алгоритмов является представление любой альтернативы решения в виде кодовой строки фиксированной длины, большинство манипуляции с которой производится в отсутствие всякой связи с ее смысловой интерпретацией. В теории генетических алгоритмов применяется определенная терминология.

Ген (свойство) – атомарный элемент хромосомы. Ген может быть битом, числом или неким другим объектом.

Хромосома (цепочка) – упорядоченная последовательность генов.

Генотип (код) – упорядоченная последовательность хромосом.

Особь (индивидуум) – конкретный экземпляр генотипа.

Фенотип – аргумент (аргументы) целевой функции, соответствующий генотипу (т. е. интерпретация генотипа с точки зрения решаемой задачи).

В наиболее распространенном случае генотип состоит из одной хромосомы и представляется в виде битовой строки. Тогда ген – это бит; генотип (хромосома) – битовая строка, заданной размерности и с определенным положением битов; особь – конкретный набор битов (0 и 1).

Поиск решения задачи с помощью генетического алгоритма, как в большинстве методов математическом программирования, заключается в использовании итерационной процедуры, когда исходное решение с каждой итерацией постепенно улучшается. В отличие от методов математического программирования на каждой итерации рассматриваются сразу несколько альтернативных вариантов (особей) решения задачи. Совокупность особей, используемых в итерации, называется популяцией.

На каждой итерации генетический алгоритм обновляет популяцию путем создания новых особей и уничтожения худших. Генерация новых особей происходит на основе моделирования процесса размножения с помощью оператора скрещивания. Порождающие особи называются родителями, а порожденные – потомками. Выбор родителей (пары кодовых строк) для скрещивания выполняется случайным образом. При этом один родитель может участвовать в нескольких скрещиваниях и необязательно, чтобы все родители участвовали в размножении. Более того, раз выбор родителей выполняется случайным образом, то может получиться, что одна особь скрещивается сама с собой. Родительская пара, как правило, порождает пару потомков. Непосредственная генерация новых кодовых строк из двух выбранных происходит за счет обмена между родителями случайно выбранными наборами генов.

Моделирование процесса мутации новых особей осуществляется за счет работы оператора мутации, применяемого к случайно выбранным потомкам за счет изменения случайного выбранного гена (генов).

Поскольку размер популяции фиксирован, то порождение потомков должно сопровождаться уничтожением особей. Выбор лучших («жизнеспособных») особей из числа родителей и потомков выполняется в операторе редукции, который уничтожает худшие («малоприспособленные») особи. Основным правилом отбора является закон эволюции: «выживает сильнейший», который обеспечивает улучшение искомого решения.

Операторы скрещивания, мутации и редукции называют генетическими операторами. Скрещивание и мутация выполняются с использованием элементов случайности, а редукция – по строго определенным правилам.

Общая схема работы алгоритма представлена на рис. 40.

Создание исходной популяции

Размножение родителей и создание потомков (оператор скрещивания)

Сокращение расширенной популяции до исходного размера (оператор редукции)

Определение лучшей особи в конечной популяции

Да

Нет

Начало

Мутация потомков (оператор мутации)

Критерий остановки выполнен?

Конец

Рис. 40. Общая схема работы генетического алгоритма

Критерием остановки работы генетического алгоритма может быть одно из следующих событий:

· сформировано заданное число поколений;

· исчерпано время, отведенное на эволюцию;

· популяция достигла заданного качества (значение критерия одной (нескольких, всех) особей превысило заданный порог);

· достигнут некоторый уровень сходимости (особи в популяции стали настолько подобными, что дальнейшее их улучшение происходит чрезвычайно медленно);

· и т. д.

5.2. Лабораторная работа № 9. Решение оптимизационной задачи
с использованием генетического алгоритма

Цель работы:освоение методов эволюционных вычислений на примере генетического алгоритма.

Описание задачи и пример ее решения

А. Описание задачи

Целевая функция задана выражением f(x) = 25 + 10x – 46x² + x³. Требуется найти максимальное и минимальное значение целевой функции в интервале x Î [-10, 53].

Б. Решение с помощью математического анализа (точный метод решения оптимизационных задач)

Очевидно, что данную задачу можно решить с помощью методов математического анализа. Последовательность решения выглядит следующим образом.

1. Определение первой производной: f’(x) = 10 – 92x + 3x².

2. Определение корней квадратного уравнения 10 – 92x + 3x² = 0: x₁ = 30.558, x₂ = 0.109.

3. Определение второй производной: f”(x) = –92 + 6x.

4. Определение типа экстремумов:

· f”(30.558) = –92 + 6 × 30.558 = 91.348 > 0 ® минимум;

· f”(0.109) = –92 + 6 × 0.109 = –91.348 < 0 ® максимум.

5. Определение значений функции в точках экстремумов:

· f(30.558) = 25 + 10 × 30.558 – 46 × 30.558² + 30.558³ = -14089;

· f(0.109) = 25 + 10 × 0.109 – 46 × 0.109² + 0.109³ = 25.5.

6. Определение значений функции на границах интервала:

· f(-10) = 25 + 10 × (-10) – 46 × (-10)² + (-10)³ = -5675;

· f(53) = 25 + 10 × 53 – 46 × 53² + 53³ = 20218.

7. Определение максимального и минимального значений целевой функции:

· максимум: y_max = MAX(-14089, 25.5, -5675, 20218) = 20218 при
x = 53;

· минимум: y_min = MIN(-14089, 25.5, -5675, 20218) = -14089 при
x = 0.56.

Результаты расчетов подтверждаются графиком функции рис. 41.

В. Решение с помощью генетического алгоритма (эвристический метод решения оптимизационных задач)

Несмотря на то, что точное решение может быть легко найдено методами математического анализа, ниже приводится решение задачи с помощью генетического алгоритма на примере одной итерации вычисления максимального значения целевой функции.

Вариант решения задачи (особь) можно представить в виде битовой строки, которая будет соответствовать целочисленному значению x в заданном интервале. Таким образом, ген – это отдельный бит строки, хромосома – последовательность из 6 битов, генотип состоит из одной хромосомы (генотип Û хромосома), фенотип – десятичное представление битовой строки минус 10.

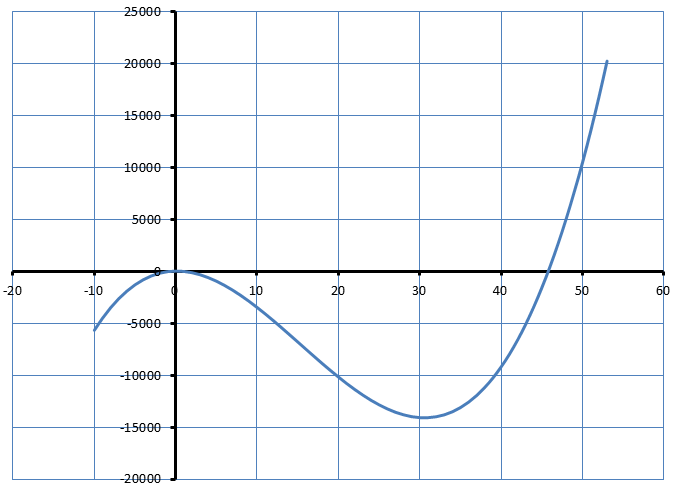
Рис. 41. График функции f(x) = 25 + 10x – 46x² + x³ в интервале x Î [-10, 53]

Пусть размер популяции будет 4 особи, число скрещиваний – 2, число мутаций – 1 потомок на поколение. Процесс мутации заключается в инверсии одного из битов строки, выбираемого случайно.

1. Случайным образом генерируются особи исходной популяции
(табл. 11).

Таблица 11

Исходная популяция

№	Представление особи	Фенотип, x	Значение целевой функции, f(x) = a + bx + cx2 + dx3
битовое	десятичное
				-8186
				-12407
			-6	-1355

2. Первая итерация – оператор скрещивания. Для скрещивания случайным образом выбраны две пары особей (1, 2) и (2, 4). В каждой паре разбиение на подстроки происходит независимо от другой пары и случайным образом. Потомки получаются в результате объединения левой подстроки одного родителя с правой подстрокой другого (табл. 12).

Таблица 12

Популяция после скрещивания

№ пары	Родитель	Потомок
№	Битовое представление	№	Битовое представление
		01 | 1011
	10 | 0010
		1000 | 10
	1110 | 01

3. Первая итерация – оператор мутации. Для мутации случайным образом выбран потомок 7, а в нем для инверсии случайно выбран 3 бит. В результате код особи изменился с 100001 на 101001.

4. Первая итерация – оператор редукции. Отбор лучших особей из родителей и потомков выполняется по максимальным значениям целевой функции с учетом требуемого размера популяции (табл. 13).

Таблица 13