Формула полной вероятности и формулы Байеса
Следствием основных теорем теории вероятностей – теоремы сложения и теорем умножения – является так называемая формула полной вероятности.
Теорема. Пусть событие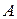 
может наступить в результате появления одного из несовместных событий 
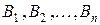, образующих полную группу. Пусть известны вероятности 
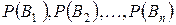и условные вероятности 
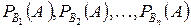. Тогда имеет место формула
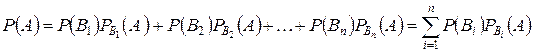, (8)
которая называется формулой полной вероятности.
Замечание 1. Так как события 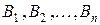образуют полную группу, то сумма их вероятностей равна единице, то есть
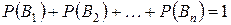, (11)
причем формула (11) служит контрольной формулой при решении задач.
Замечание 2. События 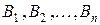называют ещё гипотезами, так как заранее неизвестно, в результате наступления какого из этих событий наступит событие .
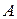Пример. По самолету производится три одиночных выстрела. Вероятность попадания при первом выстреле равна 0,4, при втором – 0,5, при третьем – 0,7. Для выхода самолета из строя заведомо достаточно трех попаданий; при одном попадании самолет выходит из строя с вероятностью 0,2, при двух попаданиях - с вероятностью 0,6. Найти вероятность того, что в результате трех выстрелов самолет будет выведен из строя.
Решение. Пусть событие 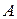- самолет выведен из строя. Рассмотрим четыре гипотезы:
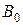- в самолет не попало ни одного снаряда,
.
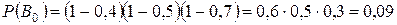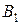- в самолет попал один снаряд,
.
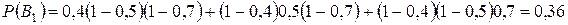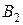- в самолет попало два снаряда,
.
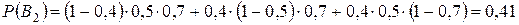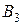- в самолет попало три снаряда,
.
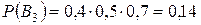Контрольная формула:
.
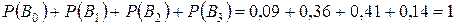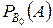- вероятность выхода самолета из строя при осуществлении гипотезы , 
.
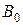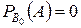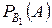- вероятность выхода самолета из строя при осуществлении гипотезы , 
.
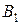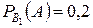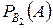- вероятность выхода самолета из строя при осуществлении гипотезы , 
.
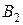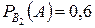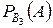- вероятность выхода самолета из строя при осуществлении гипотезы , 
.
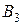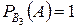Применяя формулу полной вероятности, получим:
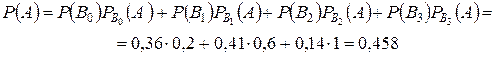
Допустим теперь, что произведено испытание, и событие 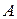уже произошло. Тогда вероятности гипотез изменятся. Определим условные вероятности этих гипотез в связи с тем, что событие 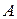наступило, то есть найдем
.
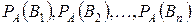По теореме умножения имеем:
.
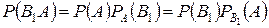Отсюда
,
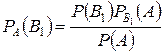подставив вместо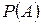 
формулу (8), получим:
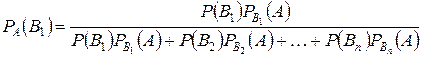
или
.
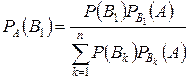Окончательно для всех гипотез
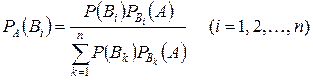(12)
Замечание. Формулы (12) называются формулами Байеса и позволяют переоценить вероятности гипотез после того, как известен результат испытания, в итоге которого появилось событие .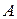
Пример. В пирамиде установлено 10 винтовок, из которых 4 имеют оптический прицел. Вероятность поражения мишени из винтовки с оптическим прицелом равна 0,95, а из винтовки без оптического прицела - 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: была взята винтовка с оптическим прицелом или без него?
Решение. Пусть событие 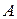- мишень поражена. Рассмотрим две гипотезы:
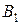- винтовка с оптическим прицелом, 
.
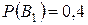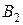- винтовка с оптическим прицелом, 
.
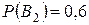Контрольная формула:
.
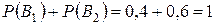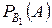- вероятность поражения мишени при осуществлении гипотезы , 
.
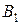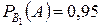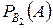- вероятность поражения мишени при осуществлении гипотезы , 
.
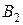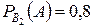Переоценим вероятности гипотез после опыта по формулам Байеса:
.
.
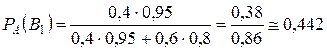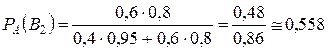Вероятнее, что цель была поражена винтовкой без оптического прицела.