Двоично-десятичное кодирование

В некоторых случаях при представлении чисел в памяти ЭВМ используется смешанная двоично-десятичная "система счисления", где для хранения каждого десятичного знака нужен полубайт (4 бита) и десятичные цифры от 0 до 9 представляются соответствующими двоичными числами от 0000 до 1001. Например, упакованный десятичный формат, предназначенный для хранения целых чисел с 18-ю значащими цифрами и занимающий в памяти 10 байт (старший из которых знаковый), использует именно этот вариант.

Представление целых чисел в дополнительном коде

Другой способ представления целых чисел — дополнительный код. Диапазон значений величин зависит от количества бит памяти, отведенных для их хранения. Например, величины типа Integer (все названия типов данных здесь и ниже представлены в том виде, в каком они приняты в языке программирования Turbo Pascal. В других языках такие типы данных тоже есть, но могут иметь другие названия) лежат в диапазоне от -32768 (-2¹⁵) до 32767 (2¹⁵ - 1) и для их хранения отводится 2 байта (16 бит); типа LongInt — в диапазоне от -2³¹ до 2³¹ - 1 и размещаются в 4 байтах (32 бита); типа Word — в диапазоне от 0 до 65535 (2¹⁶ - 1) (используется 2 байта) и т.д.

Как видно из примеров, данные могут быть интерпретированы как числа со знаком, так и без знака. В случае представления величины со знаком самый левый (старший) разряд указывает на положительное число, если содержит нуль, и на отрицательное, если — единицу.

Вообще, разряды нумеруются справа налево, начиная с 0. Ниже показана нумерация бит в двухбайтовом машинном слове.

Дополнительный код положительного числа совпадает с его прямым кодом. Прямой код целого числа может быть получен следующим образом: число переводится в двоичную систему счисления, а затем его двоичную запись слева дополняют таким количеством незначащих нулей, сколько требует тип данных, к которому принадлежит число.

Например, если число 37₍₁₀₎ = 100101₍₂₎ объявлено величиной типа Integer (шестнадцатибитовое со знаком), то его прямым кодом будет 0000000000100101, а если величиной типа LongInt (тридцатидвухбитовое со знаком), то его прямой код будет 00000000000000000000000000100101. Для более компактной записи чаще используют шестнадцатеричное представление кода. Полученные коды можно переписать соответственно как 0025₍₁₆₎ и 00000025₍₁₆₎.

· Комбинаторика и теория вероятностей. (Г)

Правило суммы и произведения. Размещение с повторениями. Размещения без повторений. Перестановки. Сочетания без повторений. Случайные события и их виды. Полная группа случайных событий. Классическое определение вероятности случайного события. Относительная часто та случайного события. Теоремы сложения и умножения вероятностей. Закон больших чисел. Теоремы Чебышева и Бернулли, их практический смысл.

Комбинаторика

Раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненным тем или иным условиям, можно составить из заданных объектов называется комбинаторикой.

На вопросы типа «Сколько всего трехзначных чисел, в которых ровно две цифры — девятки» дает ответ комбинаторика.

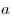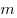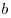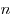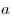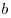Правило суммы: если элемент можно выбрать различными способами и независимо от него элемент можно выбрать различными способами, то выбрать все различные комбинации элементов « или » можно сделать 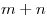способами.

Правило произведения: если элемент 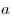можно выбрать 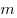различными способами и независимо от него элемент 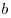можно выбрать 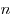различными способами, то все различные комбинации элементов « 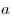и 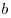» можно выбрать 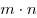способами.

Правила суммы и произведения естественным образом обобщаются и на случай комбинаций многих элементов, а именно, если первый элемент совокупности из 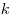различных элементов можно выбрать 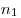способами, второй — 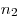способами и так далее, 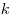-й элемент — 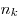способами, то всевозможных комбинаций соответственно 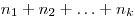и