В двоичной системе счисления (как и в других системах счисления, кроме десятичной) знаки читаются по одному. Например, число 1012 произносится «один ноль один»

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 5

Тема: Перевод информации в двоичную систему счисления

Цель: научиться переводить числа из одной системы счисления в другую; перечислять особенности и преимущества двоичной формы представления информации.

Подготовка студентов к занятию:

Ефимова О. Курс компьютерной технологии с основами информатики: Уч. пособие для старших классов/О. Ефимова, В. Морозов, Н. Угринович. – М.: ООО«Издательство АСТ»; ABF, 2002. -424.(стр. 13-18 )

Пояснения к выполнению работы:

Двоичная система счисления — позиционная система счисления с основанием 2. Благодаря непосредственной реализации в цифровых электронных схемах на логических вентилях, двоичная система используется практически во всех современных компьютерах и прочих вычислительных электронных устройствах. Алфавит этой системы счисления - цифры от 0 до 1.

В двоичной системе счисления (как и в других системах счисления, кроме десятичной) знаки читаются по одному. Например, число 1012 произносится «один ноль один».

Восьмиричная система счисления (восьмиричные числа) — позиционная система счисления по целочисленному основанию 8.

Алфавит этой системы счисления - цифры от 0 до 7, то есть (0, 1, 2, 3, 4, 5, 6, 7).

Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16.

Алфавит этой системы счисления - цифры от 0 до 9 и латинские буквы от A до F, а для обозначения цифр от 10₁₀ до 15₁₀, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).

Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения

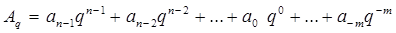(1),

где а – цифры системы счисления n и m – число целых и дробных разрядов, соответственно.

Пример: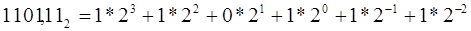

Перевод чисел из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную.

Правило перевода положительного целого десятичного числа в двоичную, восьмеричную, шестнадцатеричную систему счисления, необходимо:

1. разделить исходное число на основание системы ;

2. выделить целую часть частного и остаток. Остаток-младший разряд искомого двоичного числа. Целую часть частного принять за исходное число. Перейти к п..1.

Пример:

Число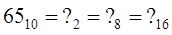

в двоичную в восьмеричную в шестнадцатеричную

в двоичную в восьмеричную в шестнадцатеричную

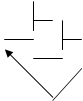
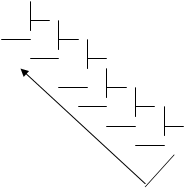
65 2 65 8 65 16

64 32 2 64 8 8 64 4

1 32 16 2 1 8 1 1

0 16 8 2 0

0 8 4 2

0 4 2 2

0 2 1

0

Ответ:

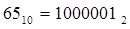
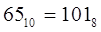
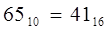
Правило перевода правильных десятичных дробей в двоичную систему состоит в следующем:

1. Умножить исходное число на основание системы 2;

2. Выделить целую и дробную части произведения. Целая часть является старшим после запятой разрядом искомой двоичной дроби. Считать дробную часть произведения исходным числом, прейти к п.1.

3. Процесс перевода заканчивается в двух случаях:

- дробная часть некоторого произведения равна 0;

- достигнута заданная точность перевода.

Пример: перевести число 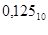в двоичную систему счисления.

0,125*2=0,250 /0

0,25*2=0,5 /0

0,5*2=1,0 /1

Ответ: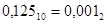

Перевод из двоичной в десятичную:

Для перевода из двоичной системы счисления в десятичную воспользуемся формулой (1), где q=2 и А=1110011:

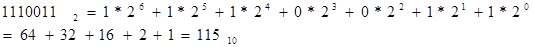
Двоичная арифметика

0+0=0 1+0=1 0-0=0 1-1=0 0*0=0 1*0=0

0+1=1 1+1=10 1-0=1 10-1=1 0*1=0 1*1=1

Таблица сложения
+
		10(перенос в старший разряд)

Таблица вычитания
-
	(заём из старшего разряда) 1

Пример сложения «столбиком» (14₁₀ + 5₁₀ = 19₁₀ или 1110₂ + 101₂ = 10011₂):

+

Таблица умножения

×

Пример умножения «столбиком» (14₁₀ * 5₁₀ = 70₁₀ или 1110₂ * 101₂ = 1000110₂):

×
+

Пример деления «столбиком»:

10010111₂ / 101₂

Ищем число, от старшего разряда которое первое было бы больше чем делитель. Это четырехразрядное число 1001. Оно выделено жирным шрифтом. Теперь необходимо подобрать делитель выделенному числу. И здесь мы опять выигрываем в сравнении в десятичной системой. Дело в том, что подбираемый делитель это обязательно цифра, а цифры у нас только две. Так как 1001 явно больше 101, то с делителем всё понятно это 1. Выполним шаг операции.

-

Итак, остаток от выполненной операции 100. Это меньше чем 101, поэтому чтобы выполнить второй шаг деления, необходимо добавить к 100 следующую цифру, это цифра 0. Теперь имеем следующее число:

-

1000 больше 101 поэтому на втором шаге мы опять допишем в частное цифру 1 и получим следующий результат (для экономии места сразу опустим следующую цифру).

-
	-

Третий шаг. Полученное число 110 больше 101, поэтому и на этом шаге мы запишем в частное 1. Получиться так:

-
	-
			-

Полученное число 11 меньше 101, поэтому записываем в частное цифру 0 и опускаем вниз следующую цифру. Получается так:

-

-

-

Полученное число больше 101, поэтому в частное записываем цифру 1 и опять выполняем действия. Получается такая картина:

-

-

-

-

Полученный остаток 10 меньше 101, но у нас закончились цифры в делимом, поэтому 10 это окончательный остаток, а 1110 это искомое частное.

Проверим в десятичных числах

10010011 = 147

101 = 5

10 = 2

11101 = 29

-
	-

На этом мы заканчиваем описание простейших арифметических операций, которые необходимо знать, для того, чтобы пользоваться двоичной арифметикой, и теперь попробуем ответить на вопрос "Зачем нужна двоичная арифметика". Конечно, выше уже было показано, что запись числа в двоичной системе существенно упрощает арифметические операции, но в то же время сама запись становится значительно длиннее, что уменьшает ценность полученного упрощения, поэтому необходимо поискать такие задачи, решение которых существенно проще в двоичных числах.