Преобразование заданной функции
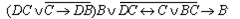
Для упрощения преобразования я разделил всю процедуру на 3 этапа.
Этап 1. Преобразование первой части функции (DC ˅ ⌐(C→DB))B. Следуя правилу замены операции импликации ⌐(C→DB) можно записать как ⌐(⌐C˅DB).По закону де Моргана ⌐(⌐C ˅(DB))=⌐⌐С⌐(DB)=C⌐(DB)=С(⌐D ˅⌐B). По закону дистрибутивности С(⌐D ˅⌐B)=C⌐D˅C⌐B.Получилось (DC ˅С⌐D˅C⌐B)B. Вынес С за скобку по закону дистрибутивности получил(D ˅⌐D ˅⌐B)BС. Сократил
D ˅⌐D ˅ по закону исключающего третьего и получил ⌐BBC, сократил ⌐BB. Остаток С и есть результат первого этапа.
Этап 2. Преобразование второй части функции ⌐ (DC↔C˅BC).Следуя закону поглощения C˅BC=С. По правилу замены эквивалентности
DC↔C=(DCC) ˅ (⌐DC⌐C). Воспользовался законом идемпотентности и сократил DCC=DC, разложил ⌐DC по закону де Моргана и получил DC˅ ((⌐D˅⌐C) ⌐C.По закону поглощения (⌐D˅ ⌐C) ⌐C=⌐C, я получил DC˅⌐C. Воспользовавшись правилом свертки DC˅⌐C=⌐C˅D. Последняя операция во второй части, это разложение по закону де Моргана и преобразование по закону двойного отрицания⌐ (⌐C˅D)=⌐⌐C⌐D=C⌐D.
Этап 3. По двум предыдущим этапам я получил общую формулу функции С˅C⌐D→B. Здесь также можно сократить по правилу сверткиС˅C⌐D =C⌐D. И окончательный результат преобразования получился f(x)= C⌐D→B.
Построение таблицы для упрощенной функции.
Для полученной функции таблица истинности построена без использования промежуточных разложений. Формула ячеек результата иметь следующий вид=ЕСЛИ(И((И(C4;НЕ(D4)))=ИСТИНА;B4=0);ЛОЖЬ;ИСТИНА).
Сравнение таблиц истинности.
Сравнение таблиц истинности выполняется с использованием функций Excel.
Формула для определения выглядит следующим образом:
=ЕСЛИ(И(L4=O4;L5=O5;L6=O6;L7=O7;L8=O8;L9=O9;L10=O10;L11=O11); "Разложение верно";"Разложение ошибочно")
Результат анализа показан на рисунке 2.
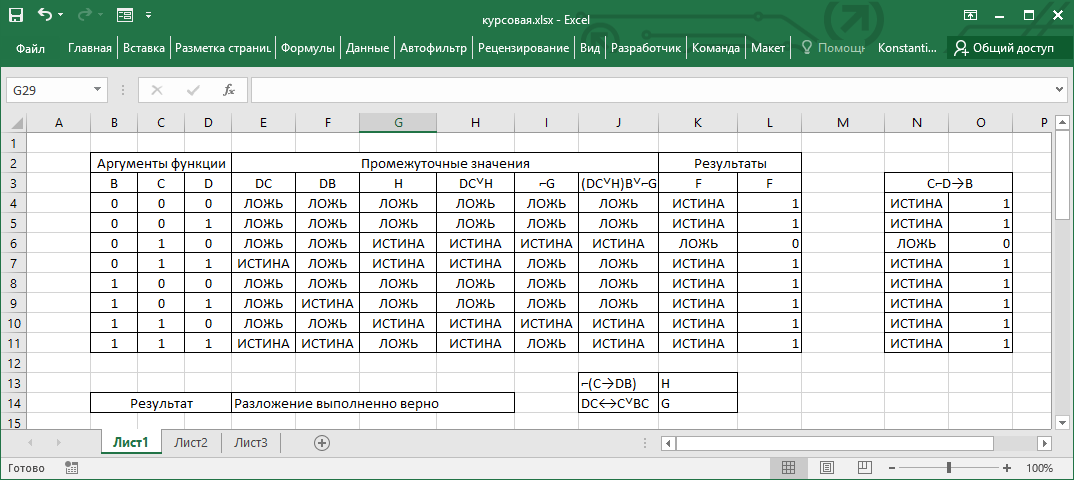
Рисунок 2 – Результат анализа разложения
Представление функции в форме СДНФ.
| B | C | D | F(B,C,D) |
Таблица 3 – Таблица истинности
В первой строке значения всех трех переменных равны 0. Следовательно первый член СДНФ рассматриваемой функции выглядит так : ⌐B⌐C⌐D
Переменные второго члена СДНФ: B=0; C=0; D=1. Второй член СДНФ равен ⌐B⌐CD.
Значение функции третьей строки равно 0. Поэтому третий член не записывается.
Переменные четвертого члена СДНФ: B=0; C=1; C=1.Четвертый член СДНФ равен ⌐BCD.
Переменные пятого члена СДНФ: B=1; C=0; D=0. Пятый член СДНФ равен B⌐C⌐D.
Переменные шестого члена СДНФ: B=1; C=0; D=1.Шестой член СДНФ равен B⌐CD.
Переменные седьмого члена СДНФ: B=1; C=1; D=0.Седьмой член СДНФ равен BC⌐D.
Переменные восьмого члена СДНФ: B=1; C=1; D=1;. Восьмой член СДНФ равен BCD.
Результат представления функции СДНФ:
F(B,C,D)= (⌐B⌐C⌐D) ˅ (⌐B⌐CD) ˅ (⌐BCD) ˅ (B⌐C⌐D) ˅ (B⌐CD) ˅ (BC⌐D) ˅ (BCD)
Упрощение формы СДНФ.
Для упрощения СДНФ формы я использовал законы алгебры логики:
- Закон поглощения A ˅ AB = A;
- Правило склеивания AB ˅ A⌐B = A;
- Правило свертки A ˅ ⌐AB = A ˅ B, ⌐A ˅ AB = ⌐A ˅ B;
- Законы де Моргана ⌐ (AB)= ⌐A ˅ ⌐B, ⌐ (A ˅ B) = ⌐A⌐B
F(B,C,D)= (⌐B⌐C⌐D) ˅ (⌐B⌐CD) ˅ (⌐BCD) ˅ (B⌐C⌐D) ˅ (B⌐CD) ˅ (BC⌐D) ˅ (BCD) =
(⌐B⌐C) ˅ (⌐BCD) ˅ (B⌐C) ˅ (B⌐C) ˅ (BC) =
(⌐B⌐C) ˅ (B⌐C) ˅ (⌐BCD) ˅ (BC) =
⌐C ˅ (⌐BCD) ˅ (BC) =
⌐C ˅ (⌐BD) ˅ (BC) =
(⌐BD) ˅ ⌐C ˅ B =
B ˅ ⌐C ˅ D.
Для проверки полученной упрощенной формы СДНФ построил таблицу истинности и сравнил с исходной таблицей. Результат таблицы истинности для полученной формы показан на рисунке 3.
Для сравнения полученной и исходной таблицы использовал формулу =ЕСЛИ(И(G5=L5;G6=L6;G7=L7;G8=L8;G9=L9;G10=L10;G11=L11;G12=L12); "Разложение верно";"Разложение ошибочно"). Результат сравнения показан на рисунке 4.
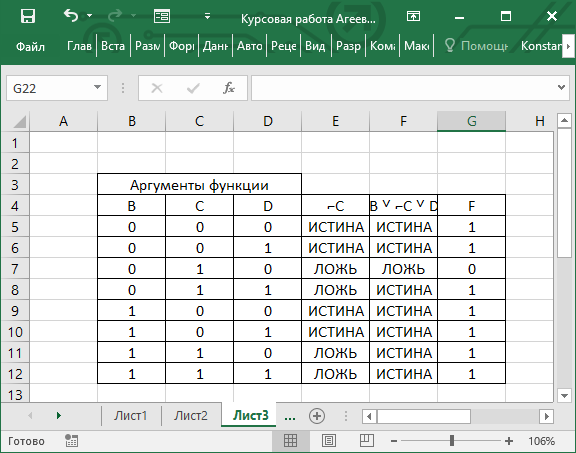
Рисунок 3 – Таблица истинности для упрощенной формы СДНФ
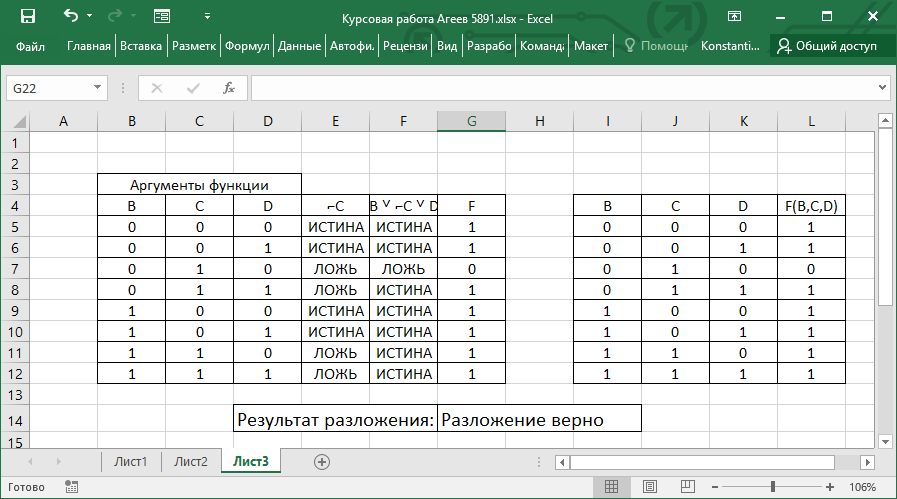
Рисунок 4 – Результат сравнения полученной таблицы
Заключение
В процессе работы освоил основные приемы работы с логическими функциями пакета MS Excel, освоил на практике изученные теоретические основы алгебры логики.
Для функции, заданной в виде аналитического выражения построил таблицу истинности. Представил функцию в форме СДНФ, упростил полученную СДНФ функцию, построил таблицу истинности для упрощенного выражения. Сравнил полученные результаты.
