Задача 10. Найти предел функции с точностью до ε.

Эта задача существенно отличается от предыдущей, и в первую очередь тем, что у функции при Z = 1 существует два предела: левый предел L равный -1, и правый предел R равный 1. Во-вторых, вещественный аргумент функции Z стремится к конечному значению 1, в то время как в предыдущем примере целочисленное n, отражающее номер члена последовательности стремилась к бесконечности. Однако алгоритм нахождения предела мы будем использовать прежний. Для этого нужно сделать преобразование исходной формулы путем замены переменных. Вместо исходного предела функции мы введем в рассмотрение два предела L и R:

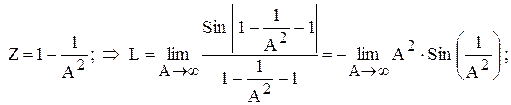(8)

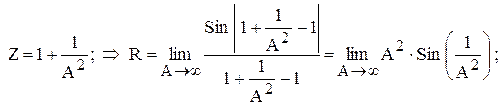(9)

На втором шаге преобразований, заменим вещественную величину A на целочисленную переменную N. И тем самым осуществим переход от предела функции к пределу последовательности 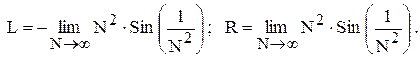(10):

(10)

Из полученных формул (10) видно, что достаточно вычислить величину правого предела R, а левый предел можно найти, положив
L = -R. Чтобы окончательно свести рассматриваемую задачу к предыдущей введем в рассмотрение последовательность 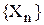, которая определена следующим образом:

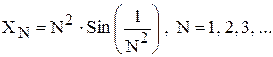(11)

Предел этой последовательности будет численно равен 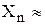R с точностью ε, если .

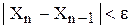После проделанных преобразований алгоритм задачи подобен алгоритму предыдущей задачи, таблица имён точно такая же. Приведем только блок-схему (рис.10) и код программы – процедуру pr10.

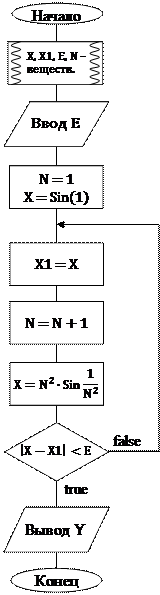Табулирование функции

Задача 11. Табулировать функцию F(X) в N равноотстоящих точках, заданную на промежутке [X₀, X_n], где

.

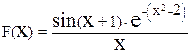Задача табулирования функции предполагает получение таблицы значений функции при изменении аргумента с фиксированным шагом. В качестве исходной информации должны быть заданы: X₀, X_n – начало и конец промежутка табулирования, при этом (X₀ <X_n); n - число интервалов разбиения промежутка [X₀, X_n]; F(X) - описание табулируемой функции.

При составлении алгоритма предполагается, что X - текущее значение аргумента; 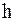- шаг изменения аргумента (иногда его называют шагом табуляции функции); 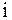- текущий номер точки, в которой вычисляются функция (i = 0 .. n).

Количество интервалов n, шаг табуляции h и величины X₀, X_n связаны между собой формулой:

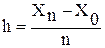(11)

Интерпретация переменных (т. е. их обозначение в математической постановке задачи, смысл и тип, обозначения в программе) приведены в таблице имен.

Математ. величина	Обозначение в программе	Содержательный смысл	Тип переменной
N	N	Число точек на интервале разбиения [X0, Xn]	целый
X0	X0	Начало промежутка	вещественный
Xn	XN	Конец промежутка	вещественный
X	X	Текущее значение аргумента	вещественный
F(X)	Y	Текущее значение функции	вещественный
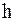	H	Шаг табулирования	вещественный

Необходимо учесть, что при некоторых значениях X функция Y не существует. В данной задаче при X = 0 функция имеет разрыв.

Блок-схема алгоритма решения задачи представлена на рис. 11.

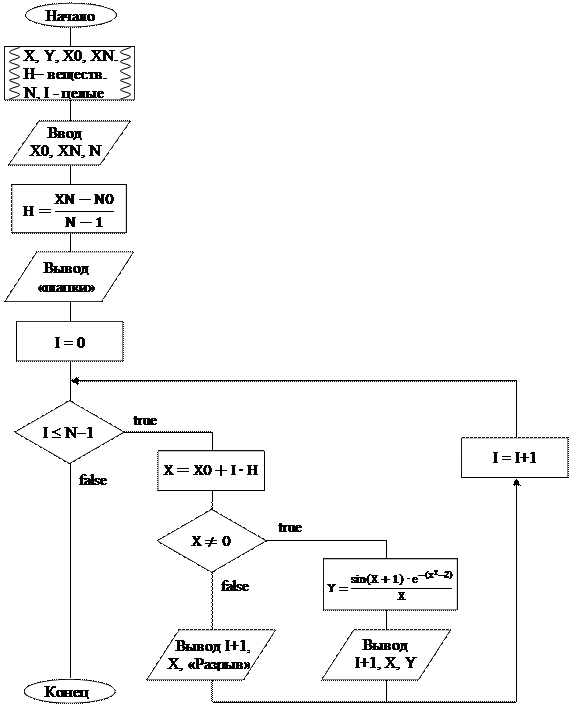Рис. 11. Блок-схема алгоритма решения задачи 11

Следует заметить, что блок-схема разрабатывается для последующей кодировки на различных алгоритмических языках программирования и может не учитывать особенности конкретного языка (способы выделения динамической памяти, особенности ввода и вывода и т. п.). Так, на блок-схеме решения данной задачи осуществляется построчный вывод номера точки, значения X и Y в цикле, но функция вывода VBA MsgBox будет выводить каждую строчку таблицы в отдельном окне. Поэтому, чтобы увидеть таблицу целиком, необходимо накапливать строки вывода в строковой переменной, которую следует вывести по окончании цикла.

Код программы представлен процедурой pr11_1.

Sub Pr11_1()

Dim X As Double, Y As Double, I As Integer, N As Integer

Dim H As Double, X0 As Double, XN As Double

Dim Prompt As String

X0 = InputBox(“Введите Xначальное”)

XN = InputBox(“Введите Xконечное”)

N = InputBox(“Введите количество точек”)

H = (XN - X0)/(N-1)

‘ Формирование “шапки”

Prompt = “N точки │ X │ Y │” & vbNewLine

Prompt = Prompt & _

“_____________________________” & vbNewLine

For I = 0 To N - 1

X = X0 + I*H;

If X <> 0 Then

Y= SIN(X+1)*EXP(2 – X^2) / X

Prompt = Prompt & “ “ & I+1 & “ │ “ & _

Format(X,##0.000) & “ │ “ & Format(Y,##0.000) & _

“ │“ & vbNewLine

Else

Prompt = Prompt & “ “ & I+1 & “ │ “ & _

Format(X,##0.000) & “ │ разрыв │“ & vbNewLine

End If

Next I

MsgBox(Prompt)

End Sub

Вывод таблицы-результата решения задачи удобно осуществлять на лист Excel. Выполним решение данной задачи с выводом результата на активный лист Excel. Блок-схема при этом не меняется, а код в модернизированном виде представлен процедурой pr11_2.

Sub Pr11_1()

Dim X As Double, Y As Double, I As Integer, N As Integer

Dim H As Double, X0 As Double, XN As Double

X0 = InputBox(“Введите Xначальное”)

XN = InputBox(“Введите Xконечное”)

N = InputBox(“Введите количество точек”)

H = (XN - X0)/(N-1)

‘ Формирование “шапки”

Cells(1, 1) = ”N точки”

Cells(1, 2) = ”X”

Cells(1, 3) = ”Y”

For I = 0 To N - 1

X = X0 + I*H;

If X <> 0 Then

Y= SIN(X+1)*EXP(2 – X^2) / X

Cells(I+2, 1) = I+1

Cells(I+2, 2) = Format(X,##0.000)

Cells(I+2, 3) = Format(Y,##0.000)

Else

Cells(I+2, 1) = I+1

Cells(I+2, 2) = Format(X,##0.000)

Cells(I+2, 3) = “разрыв”

End If

Next I

End Sub