Нахождение наибольшего и наименьшего значений.
Нахождение указанных значений функции у = f(х) выполняется в цикле, в котором вычисляется текущее значение функции и сравнивается с наибольшем или наименьшем из всех предыдущих значений этой функции. Если текущее значение функции окажется больше наибольшего из предыдущих значений, то его надо считать новым наибольшим значением. В противном случае наибольшее значение остаётся прежним. Обычно выбор начального наибольшего значения зависит от условия задачи.
Пример 4. Составить программу для нахождения наибольшего значения функции у = х sin(с х +d) при изменении аргумента х от А до В с шагом Н.
INPUT A,B,C,D,H
YMAX=-1E-10
for x =A to B step H
у=x* sin(c* x +d)
if у>YMAX then YMAX =у
next x
print YMAX
end
Пример 5. Составить программу для нахождения наименьшего элемента массива Х(50) и его порядкового номера.
option base 1
dim X(50)
for i=1 to 50
input X(i)
next i
XMIN =X(1)
for i=2 to 50
if X(i)<XMIN then XMIN=X(i) : k= i
next i
print k, XMIN
end
Простейшие алгоритмы обработки массивов.
Элементы массивов могут быть использованы для вычислений только после того, как их значения будут записаны в память ЭВМ. Простейшим способом ввода является последовательная запись вводимых элементов с помощью операторов READ-DATA. Например,
dim C(3)
READ C(0), C(1), C(2),C(3)
DATA 3.,4.86,3E-5,-1.22
В данном фрагменте программы осуществляется ввод четырёх элементов массива С. Данный способ, естественно, применим только для ввода небольшого количества элементов.
Более употребительным является ввод массива, реализованный с помощью циклического вычислительного процесса. Например,
а) DIM A(9)
for i=0 to 9
read A(i)
next
DATA 1.,2.,3.,4.,5.
DATA 6.,7.,8.,9.,10.
б) DIM(9)
for i=0 to 9
input A(i)
next
Ввод элементов двумерного массива обычно осуществляется по строкам. Например, с помощью операторов
а) DIM S(3,2)
for i=0 to 3
for j=0 to 2
read S(i, j)
next j
next i
DATA 1.,2.,3.,4.,5.,6.
DATA 7.,8.,9.,10.,11.,12.
б) DIM S(3,2)
for i=0 to 3
for j=0 to2
input S(i, j)
next j
next i
задаем массив
| 1 2 3 |
| 4 5 6 |
| 7 8 9 |
| 10 11 12 |
При большом количестве элементов в массиве удобно при использовании оператора INPUT пользоваться такой последовательностью операторов
DIM S(3,2)
for i=0 to 3
INPUT S(i,0),S(i,1),S(i,2)
next i
При этом на каждый знак вопроса печатаются через запятую и вводятся все элементы соответствующей строки.
Вывод массивов может осуществляться такими же последовательностями операторов печати PRINT.
Рассмотрим в качестве примера вывод на печать (по строкам) двумерного массива.
for i=1 to n
for j=1 to k
PRINT A(i, j)
next j
next i
Наглядность вывода может быть нарушена, если элементы массива А представляется различным числом значащих цифр. В этом случае можно предложить:
а) использование зонного формата, поставив запятую в строке с оператором PRINT вместо точки с запятой;
б) использование оператора PRINT USING.
При решении многих практических задач могут производиться различные операции над массивами. Рассмотрим примеры таких задач.
Задача 1. Сортировка элементов массива.
Выполнить сортировку элементов какого-нибудь множества – это значит упорядочить их по выбранному признаку. Число можно сортировать по величине, детали –по весу, список авторов составляется в порядке алфавита. Задача сортировки- одна из практически важных, и поэтому математики и программисты потратили немало усилий для отыскания эффективных алгоритмов её решения. Приведём пример простейшей программы сортировки чисел по их величине. В этой программе используется стандартная функция
SWAR A,B
которая меняет между собой значения двух переменных А и В одного и того же типа, что невозможно выполнить двумя последовательными операторами присваивания (А=В: В=А).
Сортировка элементов массива
INPUT N
OPTION BASE 1
DIM A(N)
for i=1 to N.
INPUT A(I)
next i
PRINT "Укажите принцип сортировки"
PRINT "По возрастанию элементов? Да или Нет"
INPUT K$
if K$="Да'' then m1
for i=1 to N-1
for j=1+i to N
if A(i)<A(j) then m2
goto m3
m2:
SWAR A(i),A(j)
m3:
next j
next i
goto m4
m1:
for i=1 to N-1
for j=1+1 to N
if A(I)>=A(J) then m5
goto m6
m5:
SWAR A(I),A(J)
m6:
next j
next i
m4:
PRINT "Печать отсортированного массива"
for k=1 to N
print A(k);
next k
end
Задача 2. Вычисление площади многоугольника.
Если координаты вершин n-угольника равны (X i, Y i), где i=0,1,…n, то площадь многоугольника может быть вычислена по формуле
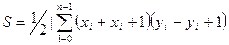
где (X0,Y0)=(X n, Y n). В программе используются переменные: N- количество вершин многоугольника; S- его площадь; X i, Y i- координаты вершин.
Площадь многоугольника.
INPUT "Количество вершин N=";N
DIM X(N), Y(N)
Print "Введите координаты(x,у) вершин"
for i=1 to N
INPUT X(i), Y(i)
next i
X(0)=X(N): Y(0)=Y(N): S=0
for i=0 to N-1
S=S+(X(i)+X(i+1))*(Y(i)-Y(i+1))
next
S=ABS(S)/2
Print "ПлощадьS="; S
end
Задача 3. Перестановка строк матрицы.
Пусть в матрице А(n, m) необходимо выполнить перестановку i-й и j-й строк. Запишем лишь фрагмент программы.
for k=1 to m
SWAR A(i, k), A(j, k)
next k
Задача 4. Преобразование матрицы в одномерный массив.
Требуется переслать элементы матрицы А(n, m) в одномерный массив Х того же размера с сохранением порядка следования по строкам.
Приведём фрагмент программы.
for i=1 to n
for j=1 to m
X((i-1)*m+ j)=A(i, j)
next j
next i
Задача 5. Поиск минимального элемента матрицы А(N,M).
Приведем лишь фрагмент программы.
P=A(1,1): k=1: L=1
for i=1 to n
for j=1 to m
if P>=A(i, j) goto m1
P=A(i, j): k= i: L= j
m1:
next j
next i
Подпрограммы и процедуры
Подпрограмма- это группа операторов или часть программы, описывающая некоторый алгоритм, который можно многократно использовать, обращаясь к нему из различных точек программы. Подпрограммы снимают те ограничения, которые имеют функции пользователя:
а) они состоят из одного оператора,
б) с их помощью можно вычислять только одно значение,
в) ими можно пользоваться только в той программе, в которой они определены.
С программами, не подозревая об этом, мы часто сталкивались в программах, записывая обращения к стандартным функциям (sin, abs, exp и т. д.). Каждая из них представляет собой небольшую программу, точнее, подпрограмму, поскольку имеет подчиненную роль в процессе счета. Обнаружив в операторе имя стандартной функции, ЭВМ вычисляет её аргумент (фактический параметр) и с этим значением переходит из программы на блок вычисления значения функции, запомнив при этом место возврата.
Для обращения к подпрограмме используют оператор
GOSUB m1
где GOSUB (перейти к программе)- имя оператора; m1- метка первого оператора подпрограммы. Любая подпрограмма должна завершаться специальным оператором возврата
RETURN
После выполнения подпрограммы оператор RETURN возвращает управление оператору, следующему за оператором GOSUB
Подпрограмма может располагаться в любом месте программы, однако удобнее размещать её в конце программы перед оператором END. Например, для вычисления корней двух квадратных уравнений вида Ах^2+Вх+0=0 может быть записана следующая программа
DATA 1.4,5.2,0.77,2.6,4.8,1.1
READ A,B,C
GOSUB m1
READ A,B,C
GOSUB m1
STOP
m1:
D=B*B-4*A*C
IF D<0 THEM PRINT "Корней нет": GOTO m3
X1=(-B+SQR(D))/(2*A)
X2=(-B-SQR(D))/(2*A)
PRINT "X1=";"X2=";X2
m3:
RETURN
END
Следует обратить внимание, что если бы в программе отсутствовал оператор STOP, то подпрограмма выполнялась бы и в третий раз, но при попытке выхода из неё произошла бы ошибка, т. к. переход на подпрограмму был осуществлен не оператором GOSUB.
Подпрограммы могут содержать обращения к другим подпрограммам. Пусть, например, требуется считать данные, подставить их в разные формулы и напечатать полученные результаты. Вычисления по формулам и печать результатов оформим как подпрограммы.
DATA 2, 4
READ A, B
GOSUB m1
STOP
m1:
X=A: Y=B
GOBUS m2
X=X^2: Y=Y^2
GOBUS m2
X=X+1/A: Y=Y-1/A
m2:
PRINT X,Y
RETURN
END
Заметим, что здесь один оператор RETURN обслуживает три оператора GOSUB. Результатом работы этой программы является следующая информация:
2 4
4 16
4,5 15,5
При использовании подпрограммы необходимо заботиться о присвоении необходимых значений входным параметром подпрограммы и о сохранении результатов её выполнения, иначе они будут испорчены при повторных обращениях к ней.
Процедурами называются части программы, ограниченные операторами SUB и END SUB. Существует формальный синтаксис объявления процедуры:
SUB имя процедуры [список параметров]
[объявление переменных]
операторы
процедуры
END SUB
Параметр "имя процедуры" задаёт имя процедуры, которое может иметь длину до 31 символа, но не может содержаться больше ни в одном операторе SUB данной программы. "Список параметров" представляет собой список формальных параметров, разделённых запятыми, которые определяют переменные передаваемые процедуре при её вызове. (Любой процедуре может быть передано не более 16 параметров).
Обращение к процедуре осуществляется с помощью оператора CALL. Рассмотрим программу, которая определяет и вызывает процедуру ADD.
SUB ADD 9(a, b, c, d)
S= a+ b+ c+ d
Print S
END SUB
w=1: x=2: y=0: z=3
CALL ADD(w, x, y, z)
Процедуру позволяют передавать в качестве аргументов целые массивы. То, что аргумент процедуру является массивом, показывается добавлением к имени переменной круглых скобок, в которых заключена числовая константа, значение которой указывает на размерность массива, но не на его размер. Проиллюстрируем это:
SUB ANNA (A(1),N,K)
'Переменная K возвращает количество нулевых
'элементов в одномерном массиве A чисел с обычной
'точностью, который содержит N+1 элемент
K=0
for i=0 to N
if A ( i )=0 then K=K+1
NEXT i
END SUB
Наличие A(1) в списке параметров определяет первый аргумент процедуры ANNA как одномерный массив. При этом ничего не сообщается о величине этого массива. Эта задача возлагается на второй аргумент- N. Вызов процедуры ANNA осуществляется следующим образом:
N=100: DIM X(N)
CALL ANNA (X(),N,L)
PRINT L
END
Затем, это Turbo Basic осуществляет контроль числа и типов аргументов в вызовах процедур и функций в программе на соответствие их числа и типу формальных параметров в соответствующих определениях. Для правильной организации взаимосвязи основной программы с подпрограммой или процедурой важно помнить, что глобальные переменные, значения которых используются до и после вхождения в программу (процедуру), могут быть в ней изменены.
Чтобы помочь решению этой проблемы, в Turbo Basic предусмотрены "локальные" переменные для процедур, которые существуют только в той программной структуре, где они объявлены. Это является достаточно веским основанием, чтобы вообще отказаться от подпрограмм. Локальные переменные могут быть массивами; просто надо задать размерность массива после того, как его имя объявлено локальным. Например, в программе
cls
option base 1
k=5
dim X(k), y(k)
for i=1 to k
read X( i )
Y( i )= X( i )
next i
data 1, 2, 3, 4, 5
CALL Dammy (X(), k s)
print "Сумма равна"; s
print x(1); x(2); x (3); x (4); x(5)
print y(1); y(2); y (3); y(4); y(5)
end
'Процедура вычисления суммы элементов массива
SUB Dammy (X(1), k, s)
LOCAL Y( )
dim Y(k)
s=0
for m=1 to k
s= s+ X(m)
Y(m)= X(m)^2
next m
END SUB
Сумма равна 15
1 2 3 4 5
1 2 3 4 5
элементы массива Y после выполнения процедуры Dammy не изменили своего значения, так как этот массив объявлен "локальным" и является рабочим в данной процедуре.
Включение процедур в исходную программу позволяет делить её на отдельные частицы, которые могут быть сохранены и использованы с другими программами.
Процедура, как отдельная часть программы, может быть сохранена на диске в виде программного файла, к которому можно обращаться с помощью специального оператора
$ INCUDE имя файла
Каждый дисковый файл имеет имя, которое может содержать до восьми символов и расширения имени, состоящего из точки, за которой следует не более трёх символов. Например,
BAI.BAS – программный файл(программа написанная на BASIK)
OPAL.PAS – программа написанная на PASCAL
MISHEL.DAT – файл данных
Использование стандартных процедур
Для решения задач матричной алгеброй
QBASIС, не содержит библиотеки стандартных подпрограмм, для решения типовых математических задач. Однако потребность в программах, реализующих стандартные математические методы, часто возникает при решении инженерно-технических и научных проблем.
В качестве иллюстрации рассмотрим использование библиотеки стандартных процедур для решения задач матричной алгеброй.
1) Процедура GMTRA производит транспонирование матрицы A размером N´M c образованием результирующей матрицы R размером M´N.
Обращение: CALL GMTRA (A( ), n1, R(), n1, n, m)
Описание параметров
N- число строк матрицы А и столбцов матрицы R;
M- число столбцов матрицы А и строк матрицы R;
n1- число элементов в матрицах А и R(n1=N´M).
Пример пользования:
$ INCLUD "GMTRA.BAS"
option base 1
cls
n=2: m=3
dim A(n, m), R(m, n)
for i=1 to n
for j=1 to m
read A(i, j): next: next
DATA 1, 2, 3, 4, 5, 6
n1=n´m
CALL GMTRA (A( ), n1, R( ),n1, n, m)
print "Результирующая матрица"
for i=1 to m
for j=1 to n
print R(i, j);
next j
next i
end
Результирующая матрица
1 4
2 5
3 6
2) Процедура GMADD производит сложение матриц А и В размером
N´M c образованием результирующей матрицы R размера N´M
Обращение: CALL GMADD (A( ), n1, B( ), n1, R( ), n1)
где n1- число элементов матриц А, В и R (n1=N´M).
Пример использования:
$ INCLUDE "GMADD.BAS"
option base 1
cls
n=2: m=3
dim A(n, m), B(n, m), R(n, m)
for i=1 to n
for j=1 to m
read A(i, j): next: next
DATA 1, 2, 3, 4, 5, 6
for i=1 to n
for j=1 to m
read B(i, j): next: next
DATA 0, 1, 0, 1, 0, 1
n1=n*m
CALL GMADD (A( ), n1, B( ), n1, R( ), n1)
print "Сумма матриц А+В=R"
for i=1 to n
for j=1 to m
print R(i, j);
next j
end
Сумма матриц А+В=R
1 3 3
5 5 7
3) Процедура GMSUB производит вычитание двух матриц А и В размером
N´M c образованием результирующей матрицы R размером N´M.
Обращение: CALL GMSUB (A( ),n1,B( ),n1,R( ),n1)
где n1- число элементов матриц А, В и R (n1=N´M)
Пример использования:
$ INCLUDE "GMSUB.BAS"
option base 1
cls
n=2: m=3
dim A(n, m),B(n, m),R(n, m)
for i=1 to n
for j=1 to m
read A(i, j): next: next
DATA 1, 2, 3, 4, 5, 6
for i=1 to n
for j=1 to m
read B(i, j): next: next
DATA 0, 1, 0, 1, 0, 1
n1=n*m
CALL GMSUB (A( ), n1, B( ), n1, R( ), n1)
print "Разность матриц А-В=R"
for i=1 to n
for j=1 to m
print R(i, j);
next j
next i
end
Разность матриц А-В=R
1 1 3
3 5
4) Процедура PGM2 вычисляет определитель det (A) матрицы А размер
N´M
Обращение: CALL PGM (n, A(), n1, D)
Описание параметров:
А- имя вводимой матрицы;
n- число строк и столбцов матрицы;
n1- число элементов матрицы A(n1-n*n);
D- значения определителя.
Примечание. После работы процедуры массива А портится.
Пример использования:
$INCLUDE "PGM2. BAS"
option base 1
cls
n=3
dim A(n, n)
for i=1 to n
for j=1 to n
read A(i, j): next: next
DATA 3, 2, 1, 5, 3, 6, 4, 3, 6
n1=n*m
CALL PGM2 (n, A( ), n1, D)
print "Определитель матрицы А равен"; D
end
Определитель матрицы А равен –8,999999046325684
5) Процедура GMPRD производит умножение матрицы А размером N´M
на матрицу В размером M´L с получением результирующей матрицы R
размером N´L.
Обращение: CALL GMPRD (A( ), n1, B( ), n2, R( ), n3, N, M, L)
Описание параметров:
N- число строк матрицы А и R;
М- число столбцов в матрице А и строк в матрице В;
L- число столбцов матриц В и R;
n1- число элементов (N*M) матрицы А;
n2- число элементов (M*L) матрицы В;
n3- число элементов (N*L) матрицы R;
Пример пользования.
$INCLUDE "GMPRD. BAS"
option base 1
cls
n=2: m=3: l=3
dim A(n, m), B(M, l), R(n, l)
for i=1 to n
for j=1 to m
read A(i, j): next: next
DATA 3, 2, 1, 2, 1, 3,4, 3, 0
n1=n*m: n2=m*l: n3=n*l
CALL GMPRD (A( ), n1, B( ), n2, R( ), n3, n, m, 1)
print "Программирование матриц А´В"
for i=1 to n
for j=1 to l
print R (i, j);
next j
next i
end
Произведение матриц А´В
19 13 7
46 31 19
6) Процедура MINV производит обращение квадратной матрицы А
порядка N.
Обращение: CALL MINV (n, A( ), n1, D)
Описание параметров:
А- имя обращаемой матрицы;
n- порядок матрицы;
n1- число элементов матрицы А(n1=n*n)
D- определитель матрицы А.
Примечание. После работы процедуры в массиве А хранится обратная матрица.
Пример использования.
$INCLUDE "MINV. BAS"
option base 1
cls
n=3
dim A(n, n)
for i=1 to n
for j=1 to n
read A(i, j): next: next
DATA 3, 2, -1, 1, 1, 2, 2, 2, 5
n1=n*m
CALL MINV (n, A( ), n1, D)
print using "Определитель матрицы А равен #. #"; D
print "Обратная матрица"
for i=1 to n
for j=1 to n
print using "###. #", A(i, j)
next j
next i
end
Определитель матрицы А равен 1.0
Обратная матрица:
1.0 -12.0 5.0
-1.0 17.0 –7.0
0.0 –2.0 1.0
7) Процедура SIMQ реализует решение системы линейных уравнений
АХ=В.
Обращение:
CALL SIMQ (n, A( ), n1, B( ), n)
Описание параметров:
n- число уравнений;
А- матрица коэффициентов при неизвестных размера N´N.
n1- число элементов матрицы А(n1=N*N);
B - столбец свободных членов (массив размерности N).
Примечание. После выполнения процедуры массивы А и В портятся; результаты (решение системы) хранятся в массиве В.
Пример использования.
$INCLUDE "SIMQ. BAS"
cls
n=3
dim A(n, n), B(n)
for i=1 to n
for j=1 to n
read A(i, j): next: next
DATA 1, 1, 1, 1, 0, -1, 1, 2, 1
For i=1 to n
read B(i): next
DATA 6, -2, 8
N1=n*m
CALL SIMQ (n, A( ), n1, B( ), n)
print "Решение системы уравнений"
for i=1 to n
print B(i);
next i
end
Решение системы уравнений
1 2 3
Заметим, что система линейных уравнений АХ=В можно решить используя известные процедуры MINV и GMPRD:
Х=А-1В
Например решение системы уравнений
|2 –4 3| |x1| |1|
| 1 3 2 | |x2| = |4|
|3 –5 4| |x3| |1|
может быть выполнено с помощью программы
$INCLUDE "MINV. BAS"
$INCLUDE "GMPRD. BAS"
option base 1
cls
n=3: m=3: l=1
dim A(n, m), B(m, l), X(n, l)
for i=1 to n
for j=1 to n
read A(i, j): next: next
DATA 2, -4, 3, 1, 3, 2, 3, -5, 4
for i=1 to n
for j=1 to l
read B(i, j): next: next
DATA 1, 4, 1
n1=n*n: n2=m*l:n3=n*l
CALL MINV (n, A( ), n1, D)
CALL GMPRD (A( ), n1, B( ), n2, X( ), n3, n, m, l)
print"Решение системы'
for i=1 to n
for j=1 to l
print using "##. #", X(i, j)
