Системы поддержки принятия решения на основе нечетких множеств

Как правило, данные, обрабатываемые в информационных системах, носят четкий, числовой характер. Однако в запросах к базам данных, которые пытается формулировать человек, часто присутствуют неточности и неопределенности.

Нет ничего удивительного, когда на запрос в поисковой системе Интернет пользователю выдается множество ссылок на документы, упорядоченных по степени релевантности запросу. Потому что текстовой информации изначально присуща нечеткость и неопределенность, причинами которой является семантическая неоднозначность языка, наличие синонимов и т.д.

Например, из базы данных требуется извлечь следующую информацию:

"Получить список молодыхсотрудников с невысокойзаработной платой"

"Найти предложения о сдаче не очень дорогогожильяблизко к центру города"

Здесь высказывания "Молодой", "Невысокая", "Не очень дорогой", "Близко" имеют размытый, неточный характер, хотя заработная плата определена до рубля, а удаленность квартиры от центра - с точностью до километра. Причиной всему служит то, что в реальной жизни мы оперируем и рассуждаем неопределенными, неточными категориями.

Концепция нечетких запросов базируется на математической теории нечетких множеств (fuzzy sets) и аппарате нечеткой логики (fuzzy logic), предложенной Л. Заде в 1965 году. Нечеткая логика - черезвычайно полезный инструмент для моделирования приближенных рассуждений. Она позволяет аккумулировать знания о некоторой предметной области, или, проще говоря, является одной из моделей представления знаний.

Нечетким множеством A в непустом четком пространстве X называется множество пар вида A={ х / MF(x) },

где MF(x) - функция принадлежности нечеткого множества A. Эта функция приписывает каждому элементу x є Х степень его принадлежности к нечеткому множеству A.

Например, формализуем нечеткое понятие А="Высокая цена на нефть" (долл. за баррель). Для этого введем область изменения значений переменной "Цена на нефть" X= [15; 30] и зададим множество пар:

A = {20/0,2; 21/0,35; 22/0,4; 23/0,5; 24/0,7; 25/0,8; 26/0,9; 27/0,95; 28/1,0; 29/1,0; 30/1,0}.

Знак "/" в данном случае не означает деление, а означает присваивание конкретным элементам множества соответствующих степеней принадлежности. Степень принадлежности не нужно путать с вероятностью, носящей объек­тивный характер и подчиняющейся другим математическим зависимостям.

Лингвистическая переменная (ЛП) — это переменная, значение которой задается набором вербальных (то есть словесных) характеристик некоторого свойства.

В общем случае лингвистическая переменная представляет собой набор, в состав которого входят:

• название лингвистической переменной (например, "Цена акции");
• универсальное множествоX, или область определения лингвистической переменной;
• множество ее значений T (базовое терм-множество), представляющих собой наименования нечетких переменных, например: "Низкая (цена)", "Высокая (цена)" и т.д.

Для задания нечетких множеств часто используют стандартные формы функций принадлежности. Наибольшее распространение получили кусочно-линейные формы, а именно: треугольная и трапецеидальная (Рис.1).

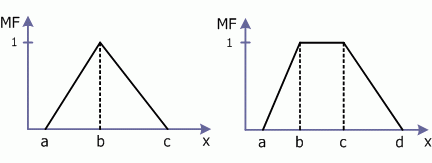
Рис. 1 Треугольная и трапецеидальная функции принадлежности

Треугольная функция принадлежности задается тройкой чисел a, b, c:

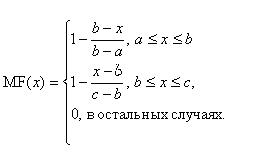
При b-a=c-b имеем случай симметричной треугольной функции принадлежности.

Аналогично трапецеидальная функция принадлежности задается четверкой чисел a, b, c, d:

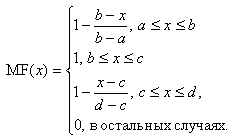
Треугольная функция принадлежности есть частный случай трапецеидальной при b=c.

Функции принадлежности для краткости записываются в виде: треугольная MF(x)=[а,в,с], трапецеидальная MF(x)= [a,b,c,d]. Определение конкретных значений a,b,c,d относится к компетенции экспертов.

Пример

Определить возраст сотрудника компании «Молодой», «Средний», «Выше среднего».

Введем лингвистическую переменную "Возраст сотрудника компании". Зададим для нее область определения X= [18; 60] и три лингвистических терма Т1,Т2,Т3 - "Молодой", "Средний", "Выше среднего".

Для термов выберем трапецеидальные функции принадлежности со следующими координатами:

"Молодой" = [18, 18, 28, 34],

"Средний" = [28, 35, 45, 50],

"Выше среднего" = [42, 53, 60, 60].

Теперь можно вычислить степень принадлежности сотрудника 30 лет к каждому из нечетких термов:

MF[Молодой](30)=0,67;

MF[Средний](30)=0,29;

MF[Выше среднего](30)=0.

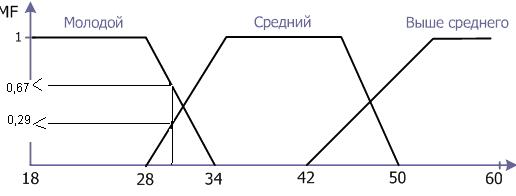
Рис.2 Функции принадлежности

Основное требование при построении функций принадлежности - значение функций принадлежности должно быть больше нуля хотя бы для одного лингвистического терма. Как правило, количество термов не превышает 7.

По такому же принципу могут быть построены функция принадлежности по оценке, например, состояния предприятия «Состояние предприятия» с термами «Очень плохое», «Плохое», «Нормальное», «Хорошее», «Очень хорошее», где по оси х может быть отложена рентабельность предприятия.

Основными потребителями нечеткой логики являются банкиры и финансисты, а также специалисты в области политического и экономического анализа. Они применяют информационные системы, использующие правила нечеткой логики, для создания моделей различных экономических, политических, биржевых ситуаций.

Начало этому процессу положила японская финансовая корпорация Yamaichi Securuties. Задавшись целью автоматизировать игру на рынке ценных бумаг, эта компания привлекла к работе около 30 специалистов по искусственному интеллекту. В первую версию системы, завершенную к началу 1990 года, вошли 600 нечетких функций принадлежности - воплощение опыта десяти ведущих брокеров корпорации. Прежде чем решиться на использование новой системы в реальных условиях, ее протестировали на двухлетней выборке финансовых данных (1987-1989 г). Система с блеском выдержала испытание. Особое изумление вызвало то, что за неделю до наступления биржевого краха (знаменитого «Черного Понедельника» на токийской бирже в 1988 году) система распродала весь пакет акций, что свело ущерб практически к нулю. После этого вопрос о целесообразности применения нечеткой логики в финансовой сфере уже не поднимался. Хотя скептики могут привести и другие примеры - например, ни одна из банковских систем не смогла предсказать падение биржевого индекса Nikkei весной 1992 года. Можно привести и другие примеры применения нечеткой логики в бизнесе. Удачный опыт Ганса по использованию экспертной системы с нечеткими правилами для анализа инвестиционной активности в городе Аахене (ФРГ) привел к созданию коммерческого программного пакета для оценки кредитных и инвестиционных рисков. На рынке коммерческих экспертных систем на основе нечеткой логики в России наиболее известным является экспертная система CubiCalc.

Нейронные сети

Нейронные сети- это раздел технологий искусственного интеллекта, в котором для обработки информации используются явления, аналогичные происходящих в нейронах живого существа. Первая модель нейронной сети была разработана в 1943 г.

Нервная система и мозг человека состоят из нейронов, соединенных между собой нервными волокнами. Нервные волокна способны передавать электрические импульсы между нейронами. Все процессы передачи раздражений от нашей кожи, ушей и глаз к мозгу, процессы мышления и управления действиями - все это реализовано в живом организме как передача электрических импульсов между нейронами.
Рассмотрим строение биологического нейрона. Каждый нейрон имеет отростки нервных волокон двух типов - дендриты, по которым принимаются импульсы, и единственный аксон, по которому нейрон может передавать импульс. Аксон контактирует с дендритами других нейронов через специальные образования - синапсы, которые влияют на силу импульса (Рис.3).

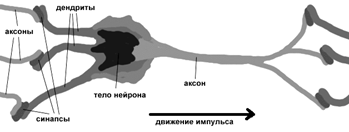
Рис. 3 Нейрон

Можно считать, что при прохождении синапса сила импульса меняется в определенное число раз, которое можно считать весом синапса. Импульсы, поступившие к нейрону одновременно по нескольким дендритам, суммируются. Если суммарный импульс превышает некоторый порог, нейрон возбуждается, формирует собственный импульс и передает его далее по аксону. Важно отметить, что веса синапсов могут изменяться со временем, а значит, меняется и поведение соответствующего нейрона.

Нетрудно построить математическую модель описанного процесса.

На рис. 4 изображена модель нейрона с тремя входами (дендритами), причем синапсы этих дендритов имеют веса w₁, w₂, w₃. Пусть к синапсам поступают импульсы силы x₁, x₂, x₃ соответственно, тогда после прохождения синапсов и дендритов к нейрону поступают импульсы w₁x₁, w₂x₂, w₃x₃. Нейрон преобразует полученный суммарный импульс:

x=w₁x₁+ w₂x₂+ w₃x₃

в соответствии с некоторой передаточной функцией f(x).

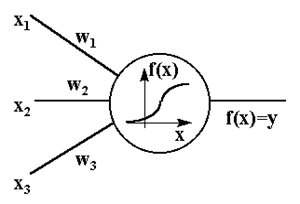Рис 4. Математическая модель нейрона

Сила выходного импульса равна:

y=f(x)=f(w₁x₁+ w₂x₂+ w₃x₃).

Таким образом, нейрон полностью описывается своими весами w_k и передаточной функцией f(x). В зависимости от вида функции f (x) и способа определения весов w i известны такие модели нейронов как модель персептрона (модель МакКаллока- Питса), нейрон сигмоидального типа, нейрон адаптивного типа, нейрон Гроссберга , нейрон Хебба и т.д.

Получив набор чисел (вектор) x_k в качестве входов, нейрон выдает некоторое число y на выходе.

Искусственная нейронная сеть (ИНС, нейросеть) -это набор нейронов, соединенных между собой. Как правило, передаточные функции f (x) всех нейронов в сети фиксированы, а веса w i являются параметрами сети и могут изменяться.

В общем случае архитектуру нейронной сети можно разделить на однослойную и многослойную модель ( Рис.5).

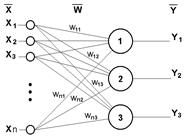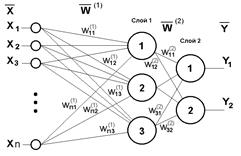а) б)

Рис.5 Однослойная (а) и многослойна (б) нейронная сеть

Основной смысл работы нейронной сети заключается в возможности классифицировать (распознавать) вектор входных сигналов X по заранее обученным образцам этого вектора. Процесс обучения происходит за счет изменения весовых коэффициентов wi.

В самом общем случае это происходит следующим образом. Из базы данных образцов выбирается побразец Xi. На выходе сети анализируется выходной вектор Yi, который должен однозначно соответствовать образцу Xi. Если соответствие не наблюдается, анализируется ошибка между выходным сигналом Yi входным сигналом Xi. В случае большой ошибки происходит корректировка соответствующих весов wi до тех пор пока ошибка не станет равной допустимой величине, процесс обучения останавливается и сеть считается обученной. Затем из базы данных выбирается другой образец Xi+1 и процесс обучения повторяется (Рис.6). Следует отметить, что для корректировки весов wi в настоящее время разработано большое количество алгоритмов.

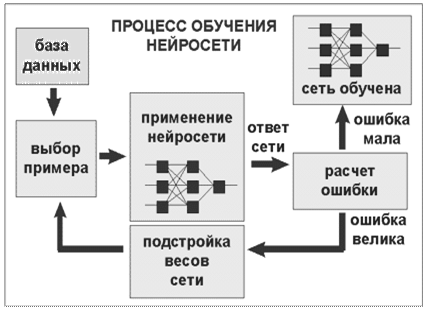
Рис.4 Процесс обучения нейронной сети

Рис.6 Процесс обучения нейрона

Пример:

Пусть имеется некоторая база данных, содержащая примеры (набор рукописных изображений букв – 33 буквы, каждая из которой изображается 900 пикселами). В этом случае нейронная сеть будет иметь 900 входов X и 33 выхода Y. Каждой букве должен соответствовать на определенном выходе Yi уровень равный «1».

Предъявляя изображение буквы "А" на вход сети, мы получаем от нее некоторый ответ, не обязательно верный. Вычисляя разность между желаемым ответом и реальным ответом сети, мы получаем 33 числа - вектор ошибки. С помощью специальных алгоритмов происходит подстройка весов wi до тех пор пока вектор ошибки не станет минимальным. Таким же образом происходит обучение для всех остальных букв.

Оказывается, что после многократного предъявления образцов веса сети стабилизируются, причем сеть дает правильные ответы на все (или почти все) образцы букв из базы данных. В таком случае говорят, что "сеть выучила все примеры", " сеть обучена", или "сеть натренирована".

После того, как сеть обучена, она может применяться для решения полезных задач. Важнейшая особенность человеческого мозга состоит в том, что, однажды обучившись определенному процессу, он может верно действовать и в тех ситуациях, в которых он не бывал в процессе обучения. Например, мы можем читать почти любой почерк, даже если видим его первый раз в жизни. Так же и нейросеть, грамотным образом обученная, может с большой вероятностью правильно реагировать на новые, не предъявленные ей ранее данные. Из приведенного выше примера можем нарисовать букву "А" другим почерком, а затем предложить обученной сети классифицировать новое изображение. Веса обученной сети хранят достаточно много информации о сходстве и различиях букв, поэтому можно рассчитывать на правильный ответ и для нового варианта изображения.

Таким образом использование нейронной сети состоит из трех основных этапов:

1. Выбор типа (архитектуры) сети.

2. Подбор весов (обучение) сети.

3. Использование обученной сети для прикладных задач.

Приведем несколько примеров использования нейронных сетей в экономических задах.

Пример:

На вход сети при обучении подавать информацию о фирме:

X1 = Работающий капитал

X2 = Сохраняемая прибыль

X3 = Прибыль до капиталовложений и налога

X4 = Рыночная стоимость акции

X5 = Величина продаж

В качестве образцов выбираются две группы фирм, одна из которых будет представлять обанкротившиеся фирмы, а другая нет, берутся их показатели для формирования входного сигнала, и обучается сеть давать ответ «банкрот» или «не банкрот».

После этого можно брать любую фирму, предъявлять ее показатели сети и сеть будет оценивать фирму как «банкрот» или «не банкрот». Может быть фирма еще не обанкротилась, но давать кредиты такой фирме опасно. Вероятность правильного ответа может достигать 80%-97%.

Пример:

Задачу прогнозирования курса акций на 1 день вперед.

Пусть у нас имеется база данных, содержащая значения курса за последние 300 дней. Простейший вариант в данном случае - попытаться построить прогноз завтрашней цены на основе курсов за последние несколько дней.

В этом случае прогнозирующая сеть должна иметь всего один выход и столько входов, сколько предыдущих значений мы хотим использовать для прогноза - например, 4 последних значения.

Образцом для обучения служит известный курс акций на пятый день после любых последовательно взятых 4- дней.

После обучения на вход нейронной сети подаются курсы последних 4- х дней и сеть определяет курс на следующий день. При увеличении количества входов достоверность прогноза будет возрастать.

Отметим, что для использования нейронных сетей в настоящее время существуют специальные программные продукты NeuroOffice, NeuroPro, NeuroInterator и д.р.