Определение кондиционных пределов параметров продуктивных пластов.

При выделении коллекторов по количественным критериям определяющими должны служить параметры, характеризующие их фильтрационные свойства: проницаемость по керну, a_сп, DIng и другие параметры по геофизическим данным. Кроме перечисленных, особо должно учитываться кондиционное значение глинистости. Такой подход обусловлен тем, что именно фильтрационные свойства пород определяют возможность получения притока в скважине. Поэтому кондиционные значения открытой пористости и нефтенасыщенности по керну не определяются.

Основным признаком, характеризующим породу как коллектор, следует считать получение из исследуемых интервалов притоков нефти или газа. Параметром, отражающим этот признак, является продуктивность скважин, q, т/сут. МПа:

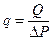(3)

где Q - суточный дебит скважины, т/сут;

DР - депрессия, МПа.

Поскольку опробованные интервалы отличаются толщиной прострела, что оказывает существенное влияние на дебит скважины, более объективной величиной следует считать удельную продуктивность скважин:

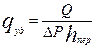(4)

h_пер – эффективная толщина перфорированного интервала пласта, м.

Для определения кондиционного предела параметров продуктивных пластов исследуется статистическая связь между удельной продуктивностью q_уд и одним из геофизических параметров, характеризующих зоны опробованных интервалов (в отличие от точечных определений керна). К числу таких параметров можно отнести a_сп, DIng, DIg, Коп_гис и т.п. При этом следует выбирать тот параметр, который в данном районе для условий исследуемого разреза является наиболее информативным. Нужно также предостеречь от определений кондиционных пределов на основе зависимости Кпр=f(q_уд), поскольку в ней исследуется связь между двумя зависимыми величинами (в формуле расчета q_уд основным параметром является дебит скважины Q, который, согласно формуле Дарси, в первую очередь, зависит от проницаемости).

В анализ по установлению кондиционного предела рекомендуется вводить данные по однородным и небольшой толщины интервалам пластов, характеризующихся минимальными значениями удельной продуктивности.

При изучении статистической связи между, например, a_сп и q_уд в качестве кондиционного принимается то значение a_сп, которому соответствует удельная продуктивность, равная 0. Другими словами, кондиционный предел a_сп равен отрезку, отсекаемому линией зависимости a_сп= f(q_уд) продолженной до пересечения с осью ординат при q_уд=0.

В этой связи немаловажную роль приобретает оценка не только тесноты, но и вида статистической связи (прямолинейной или криволинейной), поскольку при наличии криволинейной связи между параметрами прямая и кривая линии отсекут на оси ординат разные по высоте отрезки.

Оценка тесноты и вида связи между двумя параметрами производится при совместном анализе коэффициента корреляции r и корреляционного отношения h.

Коэффициент корреляции оценивает тесноту прямолинейной связи и изменяется от -1 до 0 или от 0 до +1. При тесной корреляционной связи между двумя параметрами, отождествляемой с функциональной, коэффициент корреляции равен -1 или +1, при отсутствии связи он равен 0.

Корреляционное отношение оценивает тесноту любого вида связи и изменяется от 0 до 1.

При взаимном сопоставлении r² и h² благодаря указанным выше особенностям в изменении обоих параметров, представляется возможным оценить не только тесноту, но и вид связи.

Так, если r² = h² @ 1, то связь тесная прямолинейная;

если r² < h² @ 1, то связь тесная криволинейная;

если r² = h² < 1, то связь слабая прямолинейная;

если r² < h² < 1, то связь слабая криволинейная.

Естественно, при обосновании кондиционного предела по исследуемой зависимости и при наличии связи между параметрами примерное равенство r² и h² свидетельствует о прямолинейности связи, а r² < h² - о ее криволинейности. В первом случае в качестве кондиционного принимается a_сп, отсекаемое на оси ординат прямой, а во втором случае - кривой линией.

На следующем этапе необходимо определить кондиционное значение проницаемости. Для этого исследуется статистическая связь между a_сп и десятичным логарифмом проницаемости.

Определение кондиционного предела по проницаемости необходимо для увязки полученного ранее предела a_сп с данными керна. В анализ вводятся данные по всем скважинам, где установлены a_сп и имеются определения проницаемости, независимо от того, опробовались эти интервалы или нет. Особое внимание следует обращать на обеспечение участия в анализе однородных интервалов пласта. Это требование обусловлено особенностями распределения проницаемости. Так как значения этого параметра развертываются в массовой пропорции, то распределение его в десятичных логарифмах не противоречит нормальному, т.е. имеем дело с логнормальным законом распределения. Поэтому в пределах каждого интервала в обработку включают данные о проницаемости, значения которых не превышают границ одного класса в логарифмах, которым соответствуют следующие натуральные значения: от 0,1×10^-3 мкм²; от 1×10^-3 мкм² до 10×10^-3 мкм², от 10×10^-3 мкм² до 100×10^-3 мкм² и т.д. Если в пределах одного класса содержатся единичные значения другого класса, то при расчете среднего значения по классу они не учитываются. В тех случаях, когда в пределах одного интервала пласта значения проницаемости почти поровну принадлежат двум разным классам, учитываются только значения более высокого класса.

Подготовленные таким образом значения по каждой скважине переводят в десятичные логарифмы и по ним берут среднее значение, участвующее в зависимости a_сп=f(lgКпр) для установления кондиционного предела проницаемости. Для наглядности график этой зависимости, а также связи a_сп=f(q_уд) совмещают на один чертеж. По нему и устанавливают кондиционное значение lgКпр, соответствующее кондиционному значению a_сп.

Установление кондиционных пределов a_сп и проницаемости проводится с использованием персонального компьютера в программе Microsoft Office Excel.

Для определения надежности статистической связи используется выражение

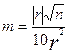(7)

где r - коэффициент корреляции (или корреляционное отношение);

n - число пар значений параметров.

Полученные значения необходимо сравнить с критическим, и если последнее окажется меньше расчетного, то можно сделать вывод о надежной статистической связи между исследуемыми параметрами.