Алгоритмы цифрового синтеза РЛИ без учета миграции дальности

Рассмотрим алгоритмы синтеза РЛИ в случае, когда миграцией дальности можно пренебречь. Для конкретности дальнейшего рассмотрения определим основные входные параметры, характеризующие сигналы на входе процессора синтеза РЛИ. Их значения являются результатами расчета режимов работы РСА с учетом выбора параметров орбиты, размеров антенны, частоты повторения положения полосы съемки, стробов приема и др.

Входными параметрами являются:

λ и f₀=c/λ - длина волны РСА и несущая частота зондирующего сигнала;
τ- длительность зондирующего импульса;

∆F- полоса спектра зондирующего ЛЧМ-сигнала;

F_p, и T_p=1/F_p - частота и период повторения импульсов;

F_s и T_s=1/F_s - частота и период дискретизации принятых сигналов;

N_τ= τ/Т_s - число отчетов в длительности импульса;

N_{r_max} - число отсчетов в стробе приема;

T_synt - время синтеза;

N_synt = T_synt/T_p - число синтезируемых импульсов;

M_R=cТ_s/2 - шаг дискретизации по наклонной дальности (масштаб голограммы и РЛИ);

R_min и R_max - наклонные дальности первого и последнего отсчетов сигнала в строке радиолокационных данных.

Излучаемый сигнал представляет собой последовательность ЛЧМ зондирующих импульсов, каждый из которых характеризуется выражением

,(4)

где rect(x) =1 при х 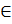[-0,5;0,5] - прямоугольная огибающая, равная единице на интервале [-0,5;0,5] и нулю в остальной области.

Для орбитального движения, как и для прямолинейного движения, длина синтезированной апертуры L_a и время синтеза T_synt определяются заданной разрешающей способностью по азимуту ρ_x

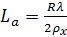; (5)

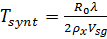, (6)

где 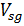- скорость перемещения носителя радиолокатора.

Принятый от одиночной точечной цели комплексный видеосигнал на выходе фазового детектора приемника в стробе приема для n-го зондирования будет иметь вид

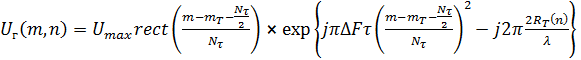, (7)

где 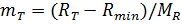- номер отсчета дальности для переднего фронта принятого импульса от цели

При аппроксимации временного закона текущей наклонной квадратичным членом азимутальные отсчеты дальности и фазы определятся формулами:

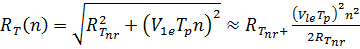; (8)

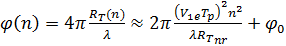,(9)

где 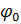-постоянная начальная фаза для данной цели

· Алгоритм прямой свертки. [5]

Фильтрация по алгоритму прямой свертки реализуется путем свертки комплексного сигнала с комплексно сопряженной двумерной дискретной опорной функцией, которая является произведением одномерных опорных функций по дальности и азимуту.

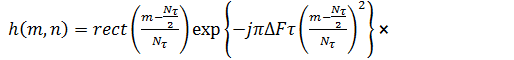
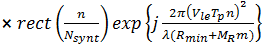, (10)

где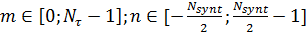

Операция свертки двумерных дискретных сигналов может быть выполнена двумя одномерными свертками - сначала по дальности, затем по азимуту.

Свертка сигнала по дальности имеет вид

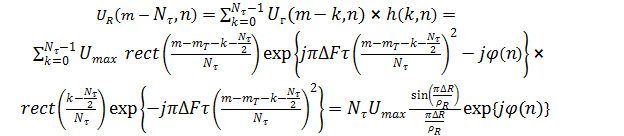, (11)

где 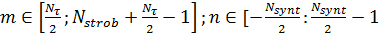], 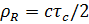; 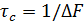- ширина импульса; 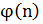- фаза азимутального отсчета; 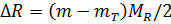- смещение выходных отсчетов относительно максимума отклика.

Максимальное значение модуля выходного сигнала при 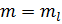будет равно 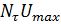. Форма отклика по дальности будет иметь вид sin(x)/х с шириной, равной 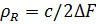. Аналогично, свертка 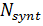отсчетов по азимуту даст двумерный отклик от точечной цели

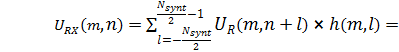
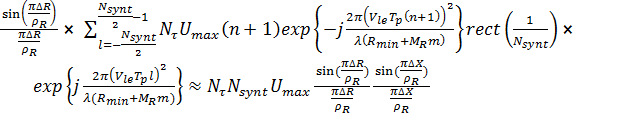, (12)

где 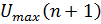– распределение амплитуды сигнала по апертуре синтеза, обусловленной формой ДН антенны радиолокатора. Форма отклика sinc соответствует 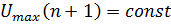, 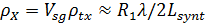– формула азимутального разрешения синтезированной апертуры

Преимущества алгоритма прямой свертки заключается в возможности непрерывной обработки всего маршрута (режим маршрутной съемки) с реализацией предельного разрешения, равного половине горизонтального размера антенны. Выходное РЛИ в координатах наклонная дальность-азимут получается с равномерным шагом по азимуту без масштабных искажений. Общим недостатком алгоритма прямой свертки является большое число комплексных операций умножения сигнала на опорную функцию и сложения. Для обработки 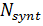строк дальности суммарное число операций 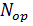можно увидеть в формуле

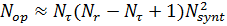, (13)

где 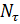- число отчетов в длительности импульса; 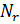- число отчетов в строке дальности.

· Алгоритм быстрой свертки. [5]

Один из самых производительных и наиболее распространенных алгоритмов – это алгоритм быстрой свертки, который реализует фильтрацию сигнала в частотной области. Он использует известное свойство преобразования Фурье, что свертке сигналов во временной области соответствует произведение спектров в частотной области. Или иначе, спектр свертки сигналов равен произведению спектров каждого из сигналов. Свертка сигнала с опорной функцией имеет вид

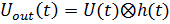; (14)

Спектр выходного сигнала

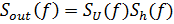, (15)

где 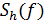– частотная характеристика фильтра

Выходной сигнал после быстрой свертки формируется в виде последовательности процедур

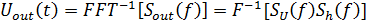,(16)

где 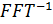- обратное преобразование Фурье

Преимущества быстрой свертки реализуются при использовании для дискретного преобразования Фурье алгоритма быстрого преобразования Фурье (БПФ).

Структурная схема алгоритма быстрой свертки представлена на рисунке 2. Он также реализуется двумя одномерными процедурами - свертка дальности и по азимуту.

Сначала получаем спектр входного сигнала 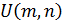и опорной функции по дальности 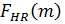методом БПФ. Выполняем свертку по дальности

, (17)

где 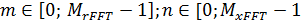], 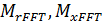– число отчетов по дальности и азимуту; 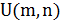- входная радиоголограмма с числом отсчетов 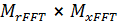, 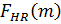- спектр опорной функции по дальности.

Делаем обратное быстрое преобразование Фурье. Дальше выполним свертку по азимуту

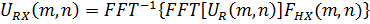; (18)

где , 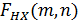- спектр опорной функции сжатия сигнала по азимуту, закон частотной модуляции которого зависит от номера отсчета по дальности.

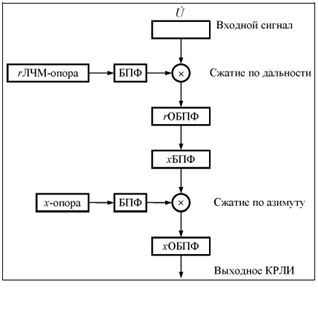
Рис.2. Алгоритм быстрой свертки

Преимуществами алгоритма быстрой свертки являются его высокая производительность, простота перестройки, получение выходного РЛИ без масштабных искажений при изменении наклонной дальности. Число требуемых операций комплексного умножения/сложения составляет примерно

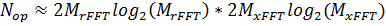(19)