Связь дирекционных углов румбов

Четверть	Значение угла	Значение румба	Наименование румба	Обратные дирекционные углы
	0° – 90°	r = α	СВ	180° – 270°
	90° – 180°	r = 180° – α	ЮВ	270° – 360°
	180° – 270°	r = α – 180°	ЮЗ	0° – 90°
	270° – 360°	r = 360° – α	СЗ	90° – 180°

Обозначения меридианов, принятые в геодезии, приведены ниже:

истинный меридиан	магнитный меридиан	осевой меридиан

Истинные меридианы разных точек линии не параллельны между собой и поэтому истинные азимуты одной и той же линии в каждой точке имеют свое значение (рис. 7).

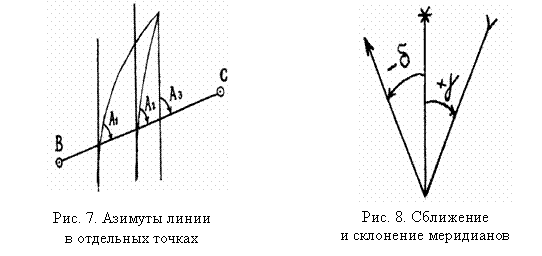
Это создает неудобство при вычислении прямоугольных координат точек. Поэтому для ориентирования геодезических сетей применяют дирекционные углы, которые в любой точке линии, в пределах зоны, одинаковы. Дирекционные углы отсчитываются от осевого меридиана, за который принимается центральный меридиан зоны в проекции Гаусса-Крюгера.

Между направлениями истинного и осевого меридианов в любой точке земной поверхности образуется угол, который называется сближением меридианов (рис.8). Сближение меридианов считается положительным, если осевой меридиан расположен к востоку от истинного меридиана, и отрицательным – к западу.

Между истинным азимутом и дирекционным углом существует зависимость

.

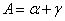(12)

Сближение меридианов приводится на картах в виде схемы под южной рамкой, слева от подписи масштабов, или может быть вычислено по формуле

,

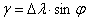(13)

где λ – разность долгот осевого и истинного меридианов данной точки; φ – широта точки.

В некоторых случаях геодезические построения приходится ориентировать по магнитному меридиану. Направление оси свободно подвешенной магнитной стрелки называется магнитным меридианом. Магнитные меридианы сходятся в магнитном полюсе Земли, который не совпадает с географическим полюсом.

Угол между направлениями истинного и магнитного меридианов называется склонением магнитной стрелки, или просто склонением (рис.8). Зависимость между истинным и магнитным азимутами имеет вид

.

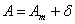(14)

Склонение считается положительным, если магнитный меридиан расположен к востоку от истинного, и отрицательным – к западу.

Величина склонения в одной и той же точке местности непрерывно меняется. Различают вековое, годичное и суточное изменения склонения. Суточное изменение склонения в средней полосе России достигает 15´. Следовательно, ориентировать геодезические сети по магнитным азимутам можно только с невысокой точностью.

При ориентировании линий используют обратные углы.

Истинный азимут A линии АВ называется прямым, ВА – обратным (рис. 9). Прямой и обратный азимуты отличаются на величину сближения меридианов.

.

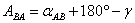(15)

Прямой и обратный дирекционный угол различаются на 180°:

.

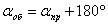(16)

Существует связь между прямым и обратным румбами. Прямой румб r_AB линии АВ отличается от обратного румба r_BA только названием. Например, r_АВ = CB:68°00, обратный румб r_ВА = ЮЗ:68°00.

При вычислении в геодезии часто используется зависимость между горизонтальными углами и дирекционными углами сторон хода.

Допустим, имеем две стороны хода АВ и ВС (рис. 10). Дирекционный угол α_AB стороны АВ будем считать известным. Если правый по ходу угол обозначить через, 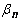то

.

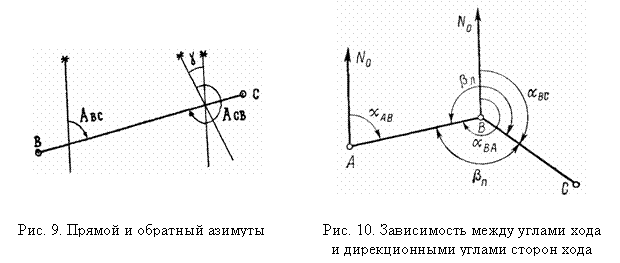
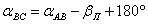(17)

.

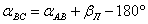(18)

· ПОНЯТИЕ О ПЛАНЕ, КАРТЕ И ПРОФИЛЕ

Земную поверхность изображают на плоскости в виде планов, карт и профилей.

При составлении планов на горизонтальную плоскость проектируют небольшие участки местности. Полученное изображение уменьшают с сохранением подобия и наносят на бумагу. Обычно в геодезии применяют метод ортогонального проектирования. Искажения, возникающие при переходе от сферы на плоскость, не превышают точности линейных измерений (1:1 000 000), и ими можно пренебречь.

Планом местности называется уменьшенное и подобное изображение горизонтальной проекции участка местности на горизонтальной плоскости.

На плане длины линий, углы и площади контуров местности не искажаются, а степень уменьшения линейных элементов постоянна для всей части плана.

Планы с изображением только предметов и контуров местности называются ситуационными, или горизонтальными.

Планы, на которых кроме ситуации изображен еще и рельеф, называются топографическими.

Основными масштабами планов являются 1:5000, 1:2000, 1:1000 и 1:500.

Для изображения на плоскости значительных частей земной поверхности или всей Земли их проектируют на поверхность эллипсоида. Полученное изображение переносят с поверхности эллипсоида на плоскость, используя для этого специальные картографические проекции, которые устанавливают зависимость между положением точек на эллипсоиде и их изображением на плоскости с учетом кривизны Земли. Для создания карт применяют равноугольную поперечно-цилиндрическую проекцию Гаусса-Крюгера. В этой проекции по определенным математическим законам строят картографическую сетку, внутри которой располагают изображение контуров местности и рельефа.

Так как при составлении карт контуры местности первоначально проектируют на эллипсоид, а затем на плоскости, то вследствие этого на карте не сохраняется полное геометрическое подобие контуров местности, также нет и постоянного масштаба на всей части карты. Это связано с тем, что сферическую поверхность нельзя развернуть на плоскости без складок и разрывов.

Таким образом, картой называется уменьшенное изображение на плоскости всей Земли или значительных ее частей с учетом кривизны Земли.

Все существующие карты делятся на общегеографические и специальные.

Общегеографические карты, в зависимости от масштаба и полноты изображения, разделяются на обзорные (масштаб мельче 1:1000000) и топографические.

Карты делятся на:

1. Мелкомасштабные 1:1000000, 1:500000.

2. Среднемасштабные 1:200000, 1:100000.

3. Крупномасштабные 1:50000, 1:25000, 1:10000.

Топографические карты являются достаточно подробными картами, по которым можно выполнять проектирование инженерных сооружений и решать ряд задач при строительстве крупных объектов.

Специальные карты отличаются от топографических детальным изображением конкретного природного комплекса (речная сеть, почвы, растительность и т.д.).

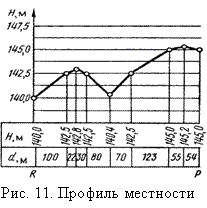
Профилем называется уменьшенное изображение на плоскости вертикального разреза местности.

Для построения профиля проводят прямую линию и строят от нее перпендикуляры, равные высоте точек местности. Концы перпендикуляров соединяют прямыми линиями (рис.11). Для лучшего чтения чертежа, перпендикуляры обычно строят в масштабе в 10–20 раз крупнее, чем масштаб карты.

· МАСШТАБЫ

Для изображения местности на плоскости необходимо горизонтальные проложения линий местности уменьшить в заданное число раз.

Степень уменьшения горизонтальных проложеных линий местности при изображении их на плане (карте) называется масштабом.

Другими словами отношение длины линии на плане (карте)d_n к длине горизонтального проложения соответствующей линии d_m на местности, называется масштабом.

Масштабы делятся на численный, пояснительный, линейный и поперечный.

Численный масштаб – дробь с числителем единица и знаменателем, показывающим степень уменьшения линии местности при изображении ее на плане 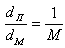(М - показатель масштаба) . Например, 1:500; 1:1000; 1:10000. Следует иметь в виду, что числитель и знаменатель выражаются в одноименных единицах. Для масштаба 1:1000, 1см на плане соответствует 1000см на местности.

Так как длины линий вычисляют в метрах, то для упрощения расчетов численный масштаб записывают в виде пояснительного масштаба.

Пояснительный масштаб – количество метров или километров, соответствующие 1 см на плане: для масштаба 1:500; в 1 см – 5 м ; для масштаба 1:1000, в 1 см – 10 м ; для масштаба 1:1000, в 1 см –10 м; для масштаба 1:10 000, в 1 см – 100 м.

Численный масштаб не всегда удобен для практических целей, так как для определения расстояний нужно выполнять расчеты. С этой целью применяют линейный и поперечный масштабы.

Линейный масштаб – графическое изображение численного масштаба. Для его построения (рис.12) проводится прямая линия, которая делится на несколько равных отрезков, называемых основанием масштаба. Как правило, оно берется равным 2 см. За начало отсчета (нуль) принимается правый конец первого основания. Вправо от него каждое основание подписывается количеством метров на местности, равным расстоянию данного штриха от нулевого. Первое основание делится на 10 равных частей.

Расстояние на линейном масштабе удобно определять с помощью циркуля-измерителя. Например, необходимо отложить на плане в масштабе 1:500 линию длиной 25,0 м. Одну ножку циркуля ставят на деление 25м, вторую на пятое деление влево от нуля. Если нужно отложить в этом масштабе доли метра, то их количество придется оценивать на глаз. Точность определения длин линий по линейному масштабу составляет 0,1 деления, для масштаба 1:500 это составит 0,1 м.

Для более точных измерений применяется поперечный масштаб (рис. 13).

Рис. 12. Линейный масштаб

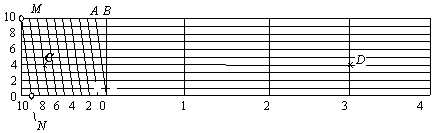
Рис. 13. Поперечный масштаб

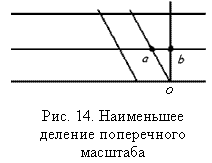
Поперечный масштаб строится в такой последовательности. Проводят прямую линию и делят ее на равные отрезки по 2 см (основание масштаба). Из конца каждого отрезка восстанавливают перпендикуляры (на стандартных масштабах высота их 25 мм), крайние из них делят на 10 частей. Через точки деления проводят прямые, параллельные основанию. Верхнее и нижнее основание левого прямоугольника делят на 10 равных частей (2 мм), которые называются ценой деления поперечного масштаба. Затем нулевую точку М верхнего основания соединяют с первой точкой N нижнего основания, далее первую точку верхнего основания со второй точкой нижнего основания и т.д. Деление ab называется наименьшим делением поперечного масштаба. На рис.14 для наглядности изображен фрагмент поперечного масштаба с делением ab.

Из подобия треугольников 0ab и 0АВ следует, что ab = 0,1АВ. По построению АВ = 0,1 от основания масштаба, следовательно, наименьшее деление поперечного масштаба ab равно 0,01 от основания или 0,2 мм.

Поперечный масштаб с основанием 2см называется нормальным, или сотенным, поперечным масштабом.

Пользоваться поперечным масштабом достаточно просто. Для определения необходимой длины линии одну ножку циркуля ведут по вертикальной линии, а вторую по наклонной до совмещения с ней. Тогда измеряемая линия складывается из трех частей: первая часть равна числу оснований, вторая – числу делений масштаба, третья – числу наименьших делений плюс или минус половина наименьшего деления.

Например, расстояние CD, отмеченное крестиками на рис.13, составляет в масштабе 1:500 – 37,4 м, а в масштабе 1:1000 – 74,8 м.

Поперечный масштаб гравируется на специальных металлических линейках или геодезических транспортирах.

Точность измерения линий на планах определяется графической, или предельной, точностью масштаба.

Длина горизонтального проложения линии местности, соответствующая на плане отрезку 0,1 мм, называется точностью масштаба. Например, точность масштаба 1:500 равна 0,1 мм × 500 = 50 мм = 5 см = 0,05 м; масштаба 1:1000 – 0,1 м; масштаба 1:2000 – 0,2 м.

Точность определения длины линии при помощи поперечного масштаба и циркуля равна 0,2 мм.

· НОМЕНКЛАТУРА КАРТ И ПЛАНОВ

В инженерной геодезии чаще всего пользуются топографическими картами. Их составляют в масштабах 1:10000, 1:25000, 1:50000 и 1:100000. Границами листов таких карт служат меридианы и параллели.

Номенклатурой называется система обозначений (нумераций) отдельных листов топографических карт (планов). В основу номенклатуры топографических карт различных масштабов положена карта масштаба 1:1000000. Для получения одного листа карты этого масштаба весь земной шар делят (рис.15) меридианами и параллелями на колонны и ряды (пояса). Протяженность колонны составляет 6 по долготе и счет ведут с запада на восток от меридиана с долготой 180. Колонны нумеруют арабскими цифрами. Протяженность ряда (пояса) составляет 4, счет ведут от эквтора к северному и южному полюсам. Ряды обозначают прописными буквами латинского алфавита. В результате этого размеры каждого листа такой карты будут равны 4° по широте (ряды) и 6° по долготе (колонны). Номенклатура каждого листа карты 1:1000000 состоит из двух индексов: большой буквы латинского алфавита, которая определяет широтный ряд – пояс, и числа, соответствующего номеру колонны. Так, Москва находится на листе N-37 (рис.15).

Для получения карты масштаба 1:500000 лист миллионной карты делят на четыре части и обозначают прописными буквами русского алфавита А, Б, В, Г (рис.16). Лист карты масштаба 1:200 000 получают делением листа миллионной карты на 36 частей: I – XXXVI. Для получения листа карты масштаба 1:100 000 каждый лист карты масштаба 1:1000000 делят на 144 части: 1 – 144.

Листы карт масштабов 1:50000, 1:25000 и 1:10000 получают из листа карты масштаба 1:100000 последовательным делением листа карты предыдущего более мелкого масштаба на четыре части и обозначают для масштаба 1:50000 – буквами A, Б, В, Г; для масштаба 1:25000 – a, б, в, г и для масштаба 1:10000 – цифрами 1, 2, 3, 4 (рис.17). На рис.16 и в табл.2 приведены номенклатура и размеры трапеций листов карт масштабов 1:1000 000 – 1:10000.

Рис. 15. Схема разграфки и номенклатуры листов карты масштаба 1:1 000 000

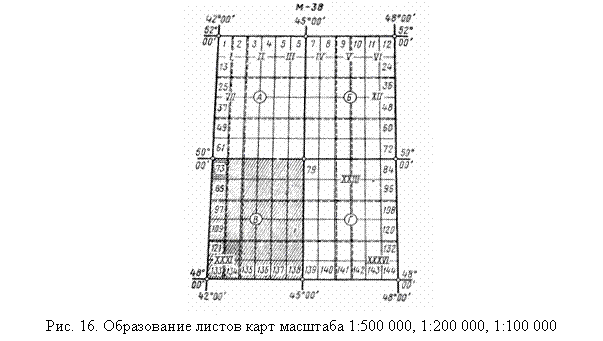
Трапецию масштаба 1:5000 получают путем деления каждого листа карты масштаба 1:100000 на 256 частей и обозначают их арабскими цифрами от 1 до 256 (рис. 17). Для получения трапеций масштаба 1:2000 каждую трапецию масштаба 1:5000 делят на 9 частей и обозначают буквами русского алфавита а, б, в, г, д, е, ж, з, и. Номенклатура трапеции масштаба 1:5000 складывается из названия соответствующего листа масштаба 1:100000 с указанием в скобках порядкового номера трапеции масштаба 1:5000, например М-38-5 (232); номенклатура трапеции масштаба 1:2000 получается из названия трапеции 1:5000 с добавлением в скобках соответствующей буквы трапеции масштаба 1:2000, например М-38-5 (232-б).

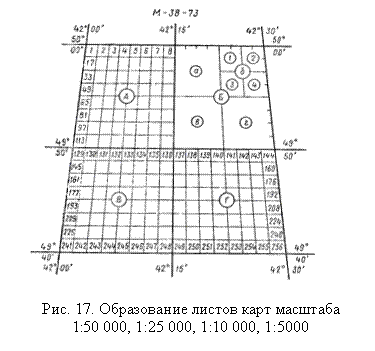
Таблица 2

Номенклатура карт

Масштаб	Номенклатура листа	Размер по
широте	долготе
1:1000000	М-38	4°	6°
1:500000	М-38-В	2°	3°
1:200000	М-38-В-XXXI	40´	60´
1:100000	М-38-73	20´	30´
1:50000	М-38-73-Б	10´	15´
1:25000	М-38-73-Б-б	5´	7´30˝
1:10000	М-38-73-Б-б-2	2´30˝	3´45˝

Согласно инструкции для топографических планов, создаваемых на участках площадью менее 20 км², применяется, как правило, прямоугольная разграфка. В основу этой разграфки положен планшет 1:5000 с размерами рамок 40×40 см, обозначаемый арабскими цифрами (рис.18). Ему соответствуют 4 листа 1:2000, каждый из которых обозначается присоединением к номеру масштаба 1:5000 одной из первых четырех заглавных букв русского алфавита (А, Б, В, Г), например 4-Б.

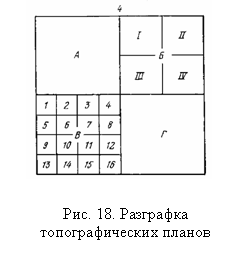
Листу масштаба 1:2000 соответствуют 4 листа масштаба 1:1000, обозначаемых римскими цифрами (I, II, III, IV), и 16 листов масштаба 1:500, обозначаемых арабскими цифрами 1, 2, 3, 4, ... 16.

Номенклатура листов масштабов 1:1000 и 1:500 складывается из номенклатуры листа масштаба 1:2000 и соответствующей римской цифры для листа масштаба 1:1000 или числа из арабских цифр для листа масштаба 1:500.

Для отдельных площадок обозначение листов топографических планов масштабов 1:1000 и 1:500 устанавливается в программе работ.

Номенклатура листов масштабов 1:5000–1:500 и размеры их рамок приведены в таблице 3.

Таблица 3

Номенклатура планов
Масштаб	Номенклатура планшета	Размеры рамок, см
1:5000		40×40
1:2000	4-Б	50×50
1:1000	4-Б-11	50×50
1:500	4-Б-15	50×50

· РЕЛЬЕФ МЕСТНОСТИ И ЕГО ИЗОБРАЖЕНИЕ НА ПЛАНАХ И КАРТАХ

·

Рельефом местности называется совокупность неровностей физической поверхности Земли.

В зависимости от характера рельефа местность подразделяют на равнинную, всхолмленную и горную.

Равнинная местность имеет слабовыраженные формы или почти совсем не имеет неровностей.

Всхолмленная местность характеризуется чередованием небольших возвышенностей и понижений.

Горная – представляет собой чередование возвышенностей более 200 м.

Все разнообразие форм рельефа можно свести к следующим основным формам.

Гора – возвышенность в виде купола или конуса. Высшая точка называется вершиной. Вершина в виде площадки называется плато, а остроконечной формы – пиком. Боковая поверхность состоит из скатов, а линия слияния скатов с окружающей местностью – подошва. Возвышенность ниже 200 м – холм.

Котловина – чашеобразное углубление замкнутое со всех сторон.Самая низкая точка котловины – дно, боковая поверхность – скаты, линия слияния скатов с равниной – бровка. Небольшая котловина называется впадиной.

Хребет – возвышенность, вытянутая в одном направлении.У хребта различают водораздельную линию (водораздел), скаты и подошву. Водораздел проходит по наиболее высоким точкам хребта.

Лощина – вытянутое в одном направлении углубление. Лощина имеет водосливную линию (тальвег), скаты и бровку. Разновидностями лощины являются долина, овраг, балка и ущелье. Расположенные по склонам лощин горизонтальные площадки называются уступами, или террасами.

Седловина – понижение между двумя соседними горными вершинами или возвышенностями. Если через седловину проходит дорога, то она называется перевалом.

Вершина горы, дно котловины, самая низкая точка седловины являются характерными точками рельефа, а водораздел и тальвег – характерными линиями рельефа.

В инженерно-строительной практике необходимо иметь план с изображением рельефа. Способ изображения рельефа на планах и картах должен обеспечивать наглядность изображения, возможность определения крутизны скатов и определение отметок точек. Существует несколько способов изображения рельефа местности:

· перспективное изображение;

· штриховка линиями разной толщины;

· отмывка разным цветом;

· отметки;

· горизонтали;

· условные знаки.

Наиболее удобным для строительства является сочетание горизонталей с отметками.

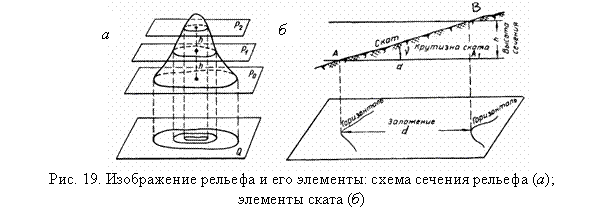
Сущность изображения рельефа горизонталями заключается в следующем (рис. 19, а). Поверхность участка Земли рассекают горизонтальными плоскостями через равные промежутки. Пересечение секущих плоскостей с поверхностью Земли образует кривые замкнутые линии, которые называются горизонталями. Горизонтали ортогонально проектируют на горизонтальную плоскость и уменьшают до размеров масштаба плана (карты). Таким образом,горизонталь – это линия равных высот.

Расстояние между горизонтальными секущими плоскостями называется высотой сечения рельефа, а расстояние между смежными горизонталями – заложением (рис. 19, б).

Наглядность изображения рельефа достигается с помощью бергштрихов, представляющих собой черточки на горизонталях, показывающих направление понижения местности, а также подписями отметок горизонталей и характерных точек местности. Верх подписи направлен в сторону повышения ската.

Горизонтали имеют следующие свойства:

· все точки, лежащие на одной горизонтали, имеют одинаковую высоту;

· горизонтали не могут пересекаться и разветвляться;

· отметки горизонталей всегда кратны высоте сечения рельефа;

· горизонталь всегда замкнутая, плавная кривая.

Как следует из свойств горизонталей, они никогда не пересекаются, за исключением: нависших камней, искусственных и естественных воронок, узких оврагов, которые не изображаются горизонталями и обозначаются условными знаками.

Для уточнения форм рельефа, если при данной высоте сечения некоторые особенности местности не могут быть выявлены, кроме основных горизонталей, соответствующих высоте сечения, также применяют:

· дополнительные (полугоризонталь) – соответствуют ½ высоты сечения рельефа, их изображают штрихами длиной 5 мм и пробелом 2 мм;

· вспомогательные – соответствуют ¼ высоте сечения рельефа, и изображаются штрихами длиной 5 мм и пробелом 1 мм.

Для упрощения чтения планов некоторые горизонтали утолщают. При высоте сечения h = 1, 2, 5 и 10 м утолщают каждую пятую горизонталь, и отметки их равны 5, 10, 25 и 50 м соответственно.

На рис. 20 приведено изображение основных форм рельефа горизонталями на плане.

При решении задач по карте необходимо установить направления ската.

Этот вопрос решают на основе следующих признаков (рис. 21):

· по указаниям бергштрихов, они всегда направлены в сторону понижения ската (рис.21, а);

· по подписям горизонталей, основания отметок всегда направлены в сторону понижения скатов (рис. 21, б);

· по подписям высот точек, например, на рис.21 (в) видно, что скат направлен с точки 2 к точке 1 (рис. 21, в);

· по объектам гидрографии, скаты всегда понижаются к рекам, озерам (рис. 21, г);

· по форме промоин: открытые стороны промоин и оврагов всегда направлены в сторону понижения местности (рис. 21, д).

· УСЛОВНЫЕ ЗНАКИ НА ПЛАНАХ И КАРТАХ

Для обозначения на планах и картах различных объектов местности применяют условные знаки. Для облегчения пользования планами и картами очертания условных знаков напоминают вид объектов местности. Условные знаки делятся на четыре группы:

· масштабные;

· внемасштабные;

· пояснительные;

· линейные.

Масштабные условные знаки изображают местные предметы с соблюдением масштаба плана, например, озера, здания, огороды и т.д. Они дают возможность определить по плану не только местоположение предмета, но и его размеры.

Внемасштабные условные знаки показывают предметы местности, которые не выражаются в масштабе плана, например, геодезические пункты, колодцы, километровые столбы и т.д.

Предметы, обозначенные такими условными знаками, занимают больше площади, чем это следует по масштабу.

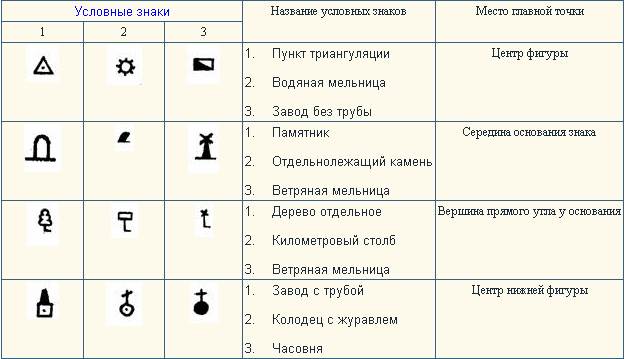
При вычерчивании внемасштабные условные знаки располагаются вертикально, точное положение пункта на местности совпадает с главной точкой. Расположение главной точки в зависимости от вида условного знака приведено в табл. 4.

Таблица 4

Расположение главной точки основных узлов

К пояснительным условным знакам относятся названия городов, сел, рек, озер, материалы сооружений, ширина дорог и т.д. Эти знаки проставляют на масштабных, внемасштабных и линейных знаках.

Линейные знаки показывают объекты линейного характера (дороги, реки, линии связи, автомобильные дороги). Длина этих объектов выражается в масштабе плана, а ширина дается внемасштабно.

Условные знаки вычерчиваются различным цветом: все предметы местности и надписи – черным; рельеф – коричневым цветом; контуры водоемов – зеленым; площади водоемов – синим.

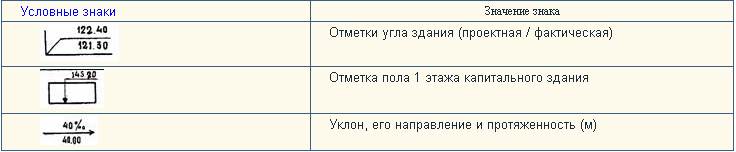
В 2000 году издательство «Недра» выпустила книгу «Условные знаки для топографических планов масштабов 1:5000, 1:2000, 1:1000 и 1:500». Они обязательны при оформлении планов для организаций, ведущих геодезические работы в Российской Федерации. Но эти условные знаки не охватывают всего многообразия требований при изображении объектов. Проектно-изыскательские и строительно-монтажные организации в дополнение к указанным знакам применяют специальные условные знаки для составления генеральных планов, разбивочных чертежей, картограмм земляных работ и др. Некоторые из условных знаков, применяемых в строительстве, приведены в таблице 5.

Таблица 5

Специальные условные знаки

· ОПРЕДЕЛЕНИЕ ПЛОЩАДЕЙ

Определение площадей участков местности выполняется графическим, аналитическим и механическим способами.

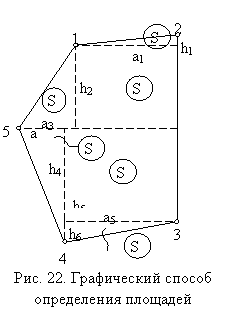
Графический способ заключается в делении участка на плане на простейшие геометрические фигуры (треугольники, четырехугольники). Значения элементов фигур определяют графически (рис. 22). При вычислении площадей пользуются известными формулами из геометрии.

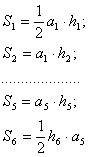(19)

Для измерения площадей криволинейных фигур применяют палетки. Палетка (рис. 23) представляет собой сетку из квадратов, нанесенных на прозрачную пленку. Сторону квадрата принимают от 1 до 5 мм в зависимости от площади контура. Для удобства подсчета на палетке через определенные промежутки проводят утолщенные линии (например, сторона наименьшей клетки равна 1 мм, а утолщенные линии проведены через 5 мм).

Площадь фигуры определяется простым подсчетом числа полных и неполных квадратов, содержащихся в данной фигуре. Установив площадь одной клетки в квадратных метрах, вычисляют общую площадь всей фигуры.

Например: площадь клетки (мм²) в масштабе 1:10000 составляет 100 м², а в масштабе 1:1000 – 1 м².

В аналитическом способе определения площадей используют натурные результаты измерения участка.

Площадь треугольника вычисляют по двум измеренным сторонам a и b треугольника и углу С между ними по формуле

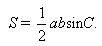(20)

Площадь четырехугольника вычисляют по измеренным диагоналям a и b четырехугольника и углу β между ними по формуле

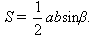(21)

Площадь параллелограмма вычисляют по основанию a и высоте h по формуле

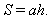(22)

Площадь трапеции находят по измеренным основаниям a и b высоте h по формуле

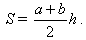(23)

В замкнутом теодолитовом ходе площадь определяют по координатам его вершин (рис. 24). Пусть даны координаты вершин треугольника. Его площадь можно определить как алгебраическую сумму трапеций:

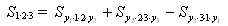или

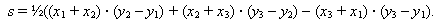(24)

После преобразования получим

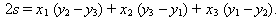Для многоугольника с n вершинами можно написать:

.

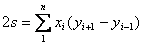(25)

Аналогично можно получить формулу

.

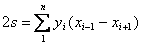(26)

Формулу (26) можно использовать для контрольных вычислений.

В таблице 6 приведен пример вычисления площади четырехугольника по координатам.

Таблица 6

Вычисление площади участка по координатам

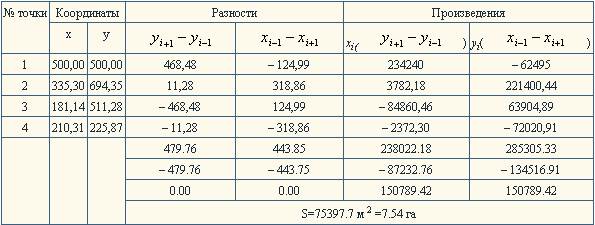
В механическом способе применяется специальный прибор – полярный планиметр (рис. 25).

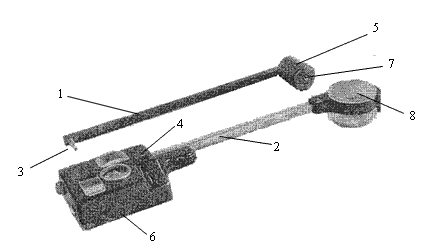
Рис. 25. Полярный планиметр

Полярный планиметр состоит из двух рычагов – полюсного 1 и обводного 2, соединяемых между собой шаровым шарниром 3, укрепленным на конце полюсного рычага и вставленным в гнездо 4 каретки 6 обводного рычага 2. На одном конце полюсного рычага прикреплен груз 5 с иглой 7. Перед началом измерений ее вдавливают в поверхность стола, на котором помещается план (карта). На конце обводного рычага имеется линза 8, на которой нанесена окружность с обводной точкой в центре.

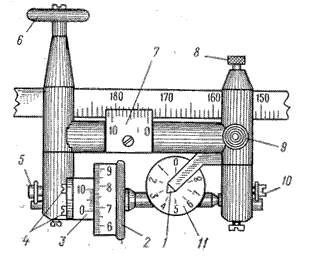
Рис. 26. Счетный механизм планиметра:
1) указатель; 2) счетное колесо; 3) верньер; 4) винты регулировки зазора между верньером и счетным колесом; 5) винт регулировки счетного колеса; 6) опорный ролик; 7) верньер шкалы обводного рычага; 8) закрепительный винт каретки счетного механизма; 9) место соединения рычагов; 10) винт регулировки счетного механизма; 11) циферблат

Каретка имеет счетный механизм (рис. 26), который состоит из счетного колеса 2, счетчика целых оборотов 11 и верньера 3. При обводе контура участка обводной точкой линзы 8 ободок счетного колеса 2, ролик 6 и обводная точка образуют три опорные точки планиметра. При этом ободок и ролик катятся или скользят по бумаге.

Делением планиметра называется одна тысячная часть окружности счетного колеса. Отсчет по планиметру состоит из четырех цифр: первая – ближайшая к указателю 1 младшая цифра счетчика оборотов; вторая и третья цифры – сотни и десятки делений, предшествующие нулевому штриху верньера; четвертая – номер штриха верньера, совпадающего с каким-либо штрихом счетного колеса. На рис.26 отчет по счетному механизму составляет n = 3684 делений.

Каретку со счетным механизмом после ослабления винта 8 можно передвигать вдоль обводного рычага 4 (рис.25), при этом меняется его длина.

Для получения надежных результатов измерений при работе планиметром должны выполняться следующие условия:

· счетное колесо должно вращаться свободно, без трения и колебаний;

· плоскость счетного колеса должна быть перпендикулярна к оси обводного рычага.

Первую поверку выполняют, удерживая обводной рычаг на весу, легким движением пальца придают вращательное движение счетному колесу (рис.26). Вращение счетного колеса должно быть быстрым и продолжительностью порядка 10–15 секунд и без колебаний. Регулировка хода счетного колеса выполняется с помощью винтов 5 и 10 (рис.26).

После регулировки хода колеса винтами устанавливают необходимый зазор между счетным колесом 2 и верньером 3 винтами 4. Величина зазора не должна превышать толщину листа кальки.

Для проверки второго условия планиметром обводят один и тот же контур при двух наложениях полюса планиметра относительно счетного механизма: «полюс лево» ПЛ и «полюс право» ПП (рис. 27).

Если смотреть со стороны обводного устройства вдоль по обводному рычагу, то при положении ПЛ полюс планиметра будет расположен слева относительно каретки 6, а при положении ПП – справа от каретки.

Разность отсчетов из двух обводов в относительной мере не должна превышать 1:200. При большем расхождении определение площади следует производить при двух положениях каретки счетного механизма и вычислять среднее арифметическое из них..

Перед измерениями определяют цену деления планиметра С. С этой целью обводят контур какой-либо правильной фигуры (квадрата, круга), площадь которой известна, и вычисляют цену деления планиметра по формуле

,

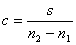(27)

где с – цена деления планиметра; S – площадь фигуры; n₂и n₁ – отсчеты по счетному механизму в начале и конце обвода контура.

При измерении планиметром соблюдают определенные правила:

· карту натягивают на столе при помощи кнопок на гладкой горизонтальной плоскости;

· полюс планиметра устанавливают вне контура, бегло обводят его, следя, чтобы угол между рычагом находился в пределах от 30º до 150º, а обводное колесо не соскальзывало с листа карты;

· выбрав начальную точку контура, совмещают с ней обводную точку, делают первый отсчет n₁ по счетному механизму и плавно обводят весь контур по ходу часовой стрелки. Обвод заканчивают в начальной точке и берут второй отсчет n₂;

· ручку обводного рычага нужно держать свободно, без напряжения;

· слегка смещают полюс и выполняют измерения, обводя контур против хода часовой стрелки, при этом получают отсчеты n₃и n₄.

Расхождение между разностями n₂ – n₁ и n₃– n₄ не должны превышать: двух единиц для площадей до 200 делений; трех единиц – до 200–2000 делений; четырех единиц – свыше 2000 делений.

Результаты измерений записывают в ведомость (табл.7). Указанные действия составляют один полуприем. Второй полуприем выполняют аналогично, но при другом положении каретки счетного механизма. Если первый полуприем был выполнен при «полюсе право», то второй выполняют при «полюсе лево».

Планиметр № Масштаб плана 1:1000;

Таблица 7

R=160,0 мм

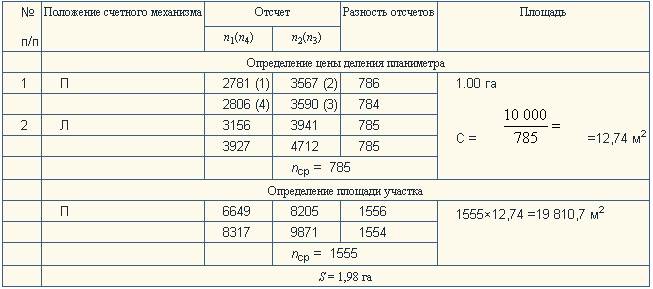
Определив среднее значение n_ср из результатов измерений обвода контура при П и Л, вычисляют цену деления планиметра С=100000/785=12,74м².

При определении площади полюс может быть установлен как внутри, так и вне контура. Если полюс находится вне контура, то необходимо определить постоянную планиметра. Для нахождения постоянной планиметра один и тот же контур обводят два раза:

· полюс устанавливают вне контура и получают площадь в делениях планиметра n₂–n₁;

· полюс устанавливают внутри контура и получают площадь .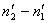

Постоянная планиметра равна разности измерений

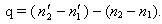(28)

Определение площади участка выполняют в том же порядке, что и при определении цены деления планиметра.

Площадь контура при положении полюса вне контура вычисляют по формуле

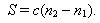(29)

Если полюс находится внутри, то вычисляют по формуле

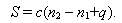(30)

Пример записи результатов измерений и вычисления площади при положении полюса вне контура приведен в таблице в табл. 7.

· ЦИФРОВАЯ МОДЕЛЬ МЕСТНОСТИ

С развитием автоматизированных систем проектирования сооружений возникла необходимость представления топографической информации в аналитическом виде. В памяти компьютера цифровые данные с местности представлены в виде координат х, у, H некоторого множества точек земной поверхности. Такое множество точек с их координатами образует цифровую модель местности (ЦММ).

По своему содержанию ЦММ разделяется:

· на цифровую модель ситуации;

· на цифровую модель рельефа.

В цифровой модели местности все элементы ситуации задаются координатами характерных точек (центров и углов зданий, сооружений, пересечения осей и т.д.).

Цифровая модель рельефа характеризует топографическую поверхность местности. Она задается множеством точек, выбранных на местности с таким расчетом, чтобы отобразить с достаточной полнотой рельеф.

Для решения этой задачи применяют различные способы составления модели местности. В одной из них, применяемой в равнинной местности, точки размещают в виде сетки квадратов. В зависимости от сложности рельефа и масштаба съемки выбирают шаг сетки. Топографическая поверхность местности аппроксимируется уравнениями второго или третьего порядка.

В другой модели на местности строится геодезическая сеть в виде линии с рядом поперечников. Точки в поперечниках располагают на характерных точках и линиях рельефа. Поверхность, в зависимости от характера местности и густоты пикетов, может быть представлена в виде плоскости или криволинейной поверхности.

Используя цифровое представление местности, с помощью компьютера легко составляются планы местности в любых масштабах, продольные профили, проекты вертикальной планировки, вычисляются объемы земляных работ и др.