Методические указания к решению задач

Решение задач по физике способствует более глубокому пони­манию изучаемого материала и помогает закреплению в памяти поня­тий, формулировок, определений, формул и физических законов, раз­вивает у студентов логическое мышление, навык в применении полу­ченных знаний для решения конкретных вопросов, имеющих практичес­кое и познавательное значение. Поэтому в данном пособии приводится список трени­ровочных задач, работа над которыми закрепит знания и навыки сту­дентов.

Задачи по физике разнообразны, и дать единый рецепт для их решения невозможно. Умение решать задачи приобретается в процес­се систематических упражнений. Можно лишь указать условия, соб­людение которых необходимо для успешного решения задач.

В основу каждой физической задачи положен тот или иной част­ный случай проявления общих законов физики. Поэтому, без твердо­го знания теории нельзя рассчитывать на успешное решение и ана­лиз даже самых простых задач.

При решениизадач необходимо:

1) хорошо вникнуть в условие задачи и установить, какие физические закономерности лежат в ее основе;

2) записать все данные в задаче физические величины в од­ной системе единиц;

3) если позволяет характер задачи, обязательно сделать чер­теж (схему), поясняющий ее сущность;

4) записать законы и формулы, на которых базируется решение, и дать словесную формулировку этих законов, разъяснить буквенные обозначения;

5) если при решении задачи применяется формула, полученная для частного случая, не выражающая какой-нибудь общий физический закон, или не являющаяся определением какой-нибудь физической величины, то ее следует вывести;

6) особое внимание следует обращать на векторный характер многих физических величин. Для полного определения таких величин необходимо учитывать не только их числовое значение, но и направ­ление;

7) получить решение задачи в общем виде, то есть выразить ис­комую величину в буквенных обозначениях величин, заданных в условии задачи. Правильность решения задачи в общем виде можно проверить, используя правило размерностей (наименований). При правильном реше­нии размерность правой части формулы совпадает с размерностью иско­мой величины. Несоблюдение этого условия (оно необходимо, но недо­статочно) свидетельствует об ошибке, допущенной в ходе решения;

8) решение задачи следует сопровождать краткими, но исчерпывающими пояснениями;

9) подставить числовые данные в полученные для искомых вели­чин формулы, произвести с ними необходимые действия. Проанализиро­вать результат (оценить его правдоподобность);

10) проводя арифметические расчеты, нужно использовать правила приближенных вычислений, позволяющие экономить время без ущерба для точности. Точность ответа не должна превышать точности, с ко­торой даны исходные величины. В тех задачах, где требуется начер­тить график, следует рационально выбрать масштаб и начало координат.

Умение решать задачи приобретается длительными и системати­ческими упражнениями. При подготовке к выполнению контрольной ра­боты следует после изучения каждой темы решить задачи из раздела "Тренировочные задачи". Они содержат элементы задач, предлагаемых для контрольных работ.

Задачи для тренировки несколько проще тех, которые входят в контрольные задания, и призваны подготовить студента к выполне­нию контрольной работы. Решение этих задач крайне полезно и не­обходимо.

При оформлении контрольных работ нужно помнить следующее.

1. Контрольная работа выполняется чернилами в обычной учени­ческой тетради.

2. Текст задачи из контрольного задания должен быть перепи­сан полностью и выписаны столбиком значения величин с их стан­дартными обозначениями.

3. При решении задач необходимо придерживаться правил, при­веденных выше.

4. Качественные задачи объяснять не односложно, а давать ис­черпывающий ответ.

ОСНОВНЫЕ ФОРМУЛЫ. ОПТИКА

Преломление света

1. Отношение синуса угла падения i₁ к синусу угла преломления i₂ для данной пары веществ есть величина постоянная, называемая относительным показателем преломления второго вещества относительно первого: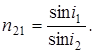

Абсолютным показателем преломления какого-либо вещества называется показатель преломления этого вещества по отношению к вакууму или воздуху.

Относительный показатель преломления второго вещества относительно первого n₂₁ равен отношению абсолютных показателей преломления этих веществ: .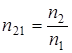

Если луч света переходит из оптически более плотного вещества (n₁) в оптически менее плотное (n₂< n₁), , то при некотором предельном значении угла падения i_пред угол преломления становится равным 90⁰, преломленный луч исчезает, а падающий испытывает полное отражение. Предельный угол определяется из формулы 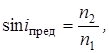где n₂ < n₁.

Интерференция света

2. Скорость света в среде 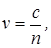где с – скорость света в вакууме; n – показатель преломления среды.

3. Оптическая длина пути луча L = nl, где l – геометрическая длина пути луча в среде с показателем преломления n.

4. Если один луч проходит путь длиной l₁ в среде с показателем преломления n₁, а другой луч – путь l₂ в среде с показателем преломления n₂, то оптическая разность хода этих лучей Δ = n₁l₁ – n₂l₂.

5. Разность фаз колебаний Δφ связана с оптической разностью хода Δ интерферирующих волн соотношением 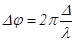, где λ – длина световой волны в вакууме.

6. Условие максимального усиления света в результате интерференции Δ = ± кλ, (к = 0, 1, 2, …).

Условие максимального ослабления света

Δ = ± (2к + 1)λ/2, (к = 0, 1, 2, …).

Дифракция света

7. Радиусы зон Френеля в случае плоского волнового фронта 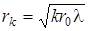, где r_k – радиус зоны, k – номер зоны (k = 1, 2, …); r₀ – расстояние от круглого отверстия в непрозрачном экране до точки наблюдения, расположенной на оси отверстия; λ – длина световой волны.

8. При дифракции параллельного пучка лучей монохроматического света на одной узкой длинной щели:

а) направления, в которых амплитуда колебаний дифрагированных лучей минимальна, определяется из условия 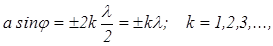где а – ширина щели; φ – угол отклонения лучей от нормали к плоскости щели, определяющий направление на дифракционный минимум; к – порядковый номер минимума; λ – длина световой волны;

б) направления, по которым амплитуда колебаний дифрагированных лучей после их интерференции максимальна, определяются по формуле .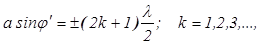

9. При дифракции на плоской дифракционной решетке направления, в которых наблюдаются максимумы света, определяются из условия

(a + b) sinφ = ± kλ; k = 0, 1, 2, …, где а – ширина прозрачной полоски (щели); b – ширина непрозрачного штриха; d = (а + b) – период решетки (или постоянная решетки); φ – угол между нормалью к поверхности решетки и направлением дифрагированных лучей; k – порядковый номер дифракционного максимума.

10. Разрешающая сила дифракционной решетки 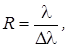где Δλ – наименьшая разность длин волн двух соседних спектральных линий (λ и

λ + Δλ), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки.

Разрешающая сила R решетки тем больше, чем больше штрихов решетка содержит и чем больше порядковый номер дифракционного максимума: R = kN, где N – полное число штрихов решетки.

11. Угловая дисперсия решетки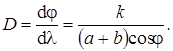

При дифракции рентгеновских лучей на кристаллической решетке направления, в которых имеет место зеркальное отражение (дифракционный максимум), определяются из уравнения Вульфа – Бреггов: 2dsinθ = kλ, где d – расстояние между атомными плоскостями кристалла; θ – угол скольжения (угол между направлением пучка параллельных рентгеновских лучей, падающих на кристалл, и гранью кристалла).

Поляризация света

12. Закон Брюстера. Луч, отраженный от поверхности диэлектрика, максимально поляризован, если тангенс угла падения i₁ луча на поверхность раздела двух сред равен относительному показателю преломления n₂₁ второй среды относительно первой: tg i₁ = n₂₁.

Закон Брюстера неприменим в случае отражения от поверхности проводников.

13. Закон Малюса. Интенсивность I плоско поляризованного света, прошедшего через анализатор, прямо пропорциональна квадрату косинуса угла α между направлением колебаний света, падающего на анализатор, и направлением колебаний, которые анализатор пропускает без ослабления: I = I₀cos²α, где I₀ – интенсивность света, падающего на анализатор.

14. Вращение плоскости поляризации. Угол поворота плоскости поляризации монохроматического света:

а) в твердых телах φ = αd, где α – постоянная вращения; d – толщина пластинки, вырезанной из твердого тела;

б) в чистых жидкостях φ = [α]ρl, где [α] – удельное вращение; ρ – плотность жидкости; l – длина столбика жидкости;

в) в растворах φ = [α]Сl, где С – концентрация раствора (масса активного вещества в единице объема раствора).