Теория относительности. 22. Зависимость массы частицы от ее скорости , где m – масса движущейся частицы; m0 –

22. Зависимость массы частицы от ее скорости 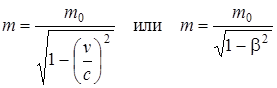, где m – масса движущейся частицы; m₀ – масса покоящейся частицы; v – скорость частицы; с – скорость света в вакууме; β – скорость частицы, выраженная в долях скорости света (β = v/c).

23. Закон пропорциональности массы и энергии. Полная энергия частицы прямо пропорциональна массе частицы E = mc², или .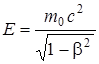

Если частица находится в покое, то, полагая β = 0, получим E₀ = m₀c², где E₀ – энергия покоя частицы.

Релятивистская формула кинетической энергии .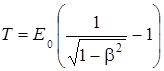

24. Импульс частицы .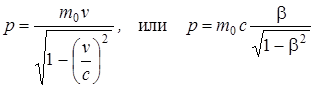

Произведение m₀c – иногда называют комптоновским импульсом частицы.

Связь между полной энергией Е, энергией покоя Е₀ и импульсом р частицы Е² = Е₀² + (рс)².

3.1. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

№ 1От двух когерентных источников S₁ и S₂ (λ = 0,8мкм) лучи попадают наэкран. На экране наблюдается интерференционная картина. Когда на пути одного из лучей перпендикулярно ему поместили мыльную пленку (n = 1,33), интерференционная картина изменилась на противоположную. При какой наименьшей толщине d_min пленки это возможно?

Р е ш е н и е.

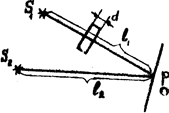Рис. 1

Изменение интерференционной картины на противоположную означает, что на тех участках, где наблюдались интерференционные максимумы, стали наблюдаться интерференционные минимумы. Такой сдвиг интерференционной картины возможен при изменении оптической разности хода лучей на нечетное число половин длин волн, т. е.

Δ₂ – Δ₁ = (2k + 1) 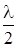, (1)

где Δ₁ - оптическая разность хода лучей до внесения пленки; Δ₂ - оптическая разность хода тех же лучей после внесения пленки; k = 0, ± 1, ±2, … .

Наименьшей толщине d_min пленки соответствует k = 0. При этом формула (1) примет вид

Δ₂ – Δ₁ = 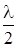. (2)

Выразим оптические разности хода Δ₂ и Δ₁. Из рис. 1 следует: Δ₁ = l₁ – l₂, Δ₂ = [(l₁ – d_min)+nd_min] – l₂ = (l₁ – l₂) + d_min(n – 1). Подставим выражения Δ₂ и Δ₁ в формулу (2):

(l₁ – l₂) + d_min(n – 1) – (l₁ – l₂) = 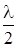, или d_min (n – 1) = .

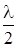Отсюда 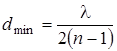. Подставив числовые значения, найде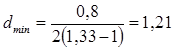м мкм.

№ 2. На стеклянный клин с малым углом нормально к его грани падает параллельный пучок лучей монохроматического света с длиной волны λ = 0,6 мкм. Число m возникающих при этом интерферен­ционных полос, приходящихся на 1 см, равно 10. Определить угол α клина.

Р е ш е н и е.

Лучи, падая нормально к грани клина, отражаются как от верхней, так и от нижней грани. Эти лучи когерентны. Поэтому на поверхности клина будут наблю­даться интер­ферен­ционные полосы. Так как угол клина мал, то отраженные лучи 1 и 2 (рис. 2) будут практически параллельны.

Темные поло­сы видны на тех участках клина, для которых разность хода лучей кратна нечетному числу половин длин волн:

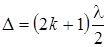(k = 0, ± 1, ± 2, …) (1)

Разность хода Δ двух лучей складывается из разности оптических длин путей (2dncosi₂) этих лучей и половины длины волны λ/2. Величина λ/2 представляет собой добавочную разность хода, возникшую при отражений луча 1 от оптически более плотной среды. Подставляя в формулу (1) значение разности хода Δ лучей, получим

2 d_k n cosi₂ + λ/2 = (2k +1) λ/2 , (2)

где n - показатель преломления стекла (n = 1,6); d_k - толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру k; i - угол преломления второго луча.

Согласно условию, угол падения равен нулю, следовательно, и угол преломления i₂ равен нулю, а соs i₂ = 1. Раскрыв скобки в правой части равенства (2), после упрощения получим

2d_kn = kλ (3)

Пусть произвольной темной полосе k-гo номера соответствует толщина d_k клина, а темной полосе (k + m) - го номера - толщина d _k+m клина. Тогда из рис. 2, учитывая, что m полос укладывается на расстоянии l, найдем

tgα = sinα = 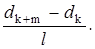(4)

Выразим из (3) d _к и d _k+m и подставимихв формулу (4). Затем, учитывая, что из-за малости угла α sinα≈α, получим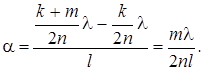

Подставляячисловые значения физических величин, найдем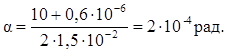

Выразим α в градусах. Для этого можно воспользоваться соотношением между радианом и секундой: 1 рад = (2,06∙10⁵) ¢¢ т.е.

α = 2∙10^-4 ∙(2,06∙10⁵) ¢¢ = 41,2¢¢.

№ 3. На дифракционную решетку нормально к ее поверхности падает монохроматический свет. Период решетки d = 2 мкм. Какого наибольшего порядка дифракционный максимум дает эта решетка в случае красного (λ₁ = 0,7 мкм) и в случае фиолетового (λ₂ = 0,41 мкм) света?

Р e ш е н и е.

На основании известной формулы дифракционной решетки напишем выражение порядка дифракционного максимума:

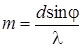, (1)

где d - период решетки; φ – угол между направлениемна дифракционный максимум и нормалью к решетке; λ - длина волны монохроматического света. Так как sinφ не может быть больше 1, то, как это следует из формулы (1), число m не может быть больше d/λ, т.е.

m ≤ d/λ. (2)

Подставив в формулу (2) числовые значения, получим: для красных лучей m ≤ 2/0,7 = 2,86; для фиолетовых лучей m ≤ 2/0,41= 4,88.

Если учесть, что порядок максимумов является целым числом, то для красного света m_max = 2 и для фиолетового m _max = 4.

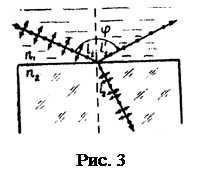
№ 4. Естественный луч света падает на полированную поверхность стеклянной пластины, погруженной в жидкость. Отраженный от пластины луч образует угол j = 97⁰ с падающим лучом (рис. 3). Определить показатель преломления n₁ жидкости, если отраженный свет максимально поляризован.

Р е ш е н и е.

Согласно закону Брюстера луч света, отраженный от диэлектрика, максимально поляризован в том случае, если тангенс угла падения численно равен относительному показателю преломления: tg i₁ = n₂₁, где n₂₁ - показатель преломления второй среды (стекла) относительно первой (жидкости).

Относительный показатель преломления равен отношению абсолютных показателей преломления. Следовательно, tg i₁ = n₂/n₁. Таккак угол падения равен углу отражения, то i₁ = φ/2 и, следовательно, tg φ/2 = n₂/n₁, откуда .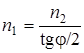

Подставив числовые значения, получим .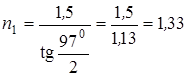

№ 6. Два николя N₁ и N₂ расположены так, что угол между их плоскостями пропускания составляет α = 60⁰. Определить, во сколько раз уменьшится интенсивность I₀ естественного света:

1) при прохождении через один николь N₁; 2) при прохождении через оба николя. Коэффициент поглощения света в николе к = 0,05. Потери на отражение света не учитывать.

Р е ш е н и е.

1. Естественный свет, падая на грань призмы Николя (рис. 4), расщепляется вследствие двойного лучепреломления на два луча: обыкновенный и необыкновенный. Оба луча одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний необыкновенного луча лежит в плоскости чертежа (плоскость главного сечения). Плоскость колебаний обыкновенного луча перпендикулярна плоскости чертежа. Обыкновенный луч 0 вследствие полного внутреннего отражения от границы АВ отбрасывается на зачерненную поверхность призмы и поглощается ею. Необыкновенный луч е проходит через призму, уменьшая свою интенсивность вследствие поглощения.

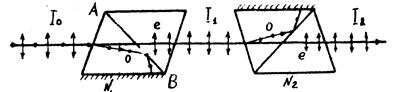
Рис. 4

I₀ – естественный луч света, I₁ = ¹/₂I₀ (1- k ), I₂ = ¹/₂I₀(1 - k)²cos²α .

Таким образом, интенсивность света, прошедшего через первую призму, I₁ = ¹/₂I₀ (1- k ).

Относительное уменьшение интенсивности света получим, разделив интенсивность I₀ естественного света, падающего на первый николь, на интенсивность I₁ поляризованного света:

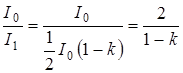. (1)

Подставив в (1) числовые значения, найдем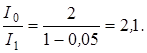

Таким образом, интенсивность уменьшается в 2,1 раза.

2. Плоско – поляризованный луч света интенсивности I₁ падает на второй николь N₂ и также расщепляется на два луча различной интенсивности: обыкновенный и необыкновенный. Обыкновенный луч полностью поглощается призмой, поэтому интенсивность его нас не интересует. Интенсивность необыкновенного луча I₂, вышедшего из призмы N₂, определяется законом Малюса (без учета поглощения света во втором николе): I₂ = I₁cos²α, где α - угол между плоскостью колебаний в поляризованном луче и плоскостью пропускания николя N₂.

Учитывая потери интенсивности на поглощение во втором николе, получим I₂ = I₁(1 - k)cos²α.

Искомое уменьшение интенсивности при прохождении света через оба николя найдем, разделив интенсивность I₀ естественного света на интенсивность I₂ света, прошедшего систему из двух николей: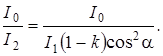

Заменяя отношение I₀/I₁, его выражением по формуле (1), получим 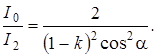Подставляя данные, произведем вычисления:

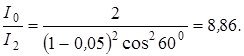
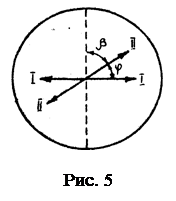Таким образом, после прохождения света через два николя интенсивность его уменьшится в 8,86 раза.

№ 6. Плоско – поляризованный монохроматический луч света падает на поля­роид и полностью им гасится. Когда на пу­ти луча поместили кварцевую пластину, интенсивность I луча света после поля­роида стала равна половине интенсивности луча, падающего на поляроид. Определить минимальную толщину кварцевой пластины. Поглощением и отражением света полярои­дом пренебречь, постоянную вращения кварца α принять равной 48,9 град/мм.

Р е ш е н и е.

Полное гашение света поляроидом означает, что плоскость пропускания поляроида (пунктирная линия на рис.5) перпендикулярна плоскости колебаний (I-I) плоско – поляризованного света, падающего на него. Введение кварцевой пластины приводит к повороту плоскости колебания света на угол φ = αl, где l – толщина пластины.

Зная, во сколько раз уменьшится интенсивность света при прохождении его через поляроид, определим угол β, который установится между плоскостью пропускания поляроида и новым направлением (II - II) плоскости колебаний падающего на поляроид плоско поляризованного света. Для этого воспользуемся законом Малюса: I = I₀cos²β.

Заметив, что β = π/2 - φ, можно написать I = I₀cos² (π/2 – φ), или

I = I₀sin²φ. (2)

Из равенства (2) с учетом (1) получим 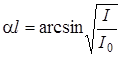, откуда искомая толщина пластины .

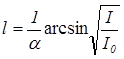Подставим числовые значения и произведем вычисления (во внесистемных единицах):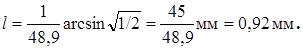

№ 7.Определить импульс Р и кинетическую энергию Т электрона, движущегося со скоростью v = 0,9c, где с - скорость света в вакууме.

Р е ш е н и е.

Импульсом частицы называется произведение массы частицы на ее скорость:

р = mv. (1)

Так как скорость электрона близка к скорости света, то необходимо учесть зависимость массы от скорости, определяемую по формуле

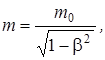(2)

где m - масса движущейся частицы; m₀ - масса покоящейся частицы; β = v/c - скорость частицы, выраженная в долях скорости света.

Заменив в формуле (1) массу m ее выражением (2) и приняв во внимание, что v = сβ, получим выражение для релятивистского импульса

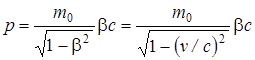, (3)

Подставим числовые значения величин, входящих в формулу (3):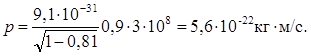

В релятивистской механике кинетическая энергия Т частицы определяется как разность между полной энергией Е и энергией покоя Е₀этой частицы, т.е. Т = Е – Е₀. Так как Е = тс² и Е₀ = m₀c², то, учитывая зависимость массы от скорости, получим 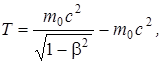или

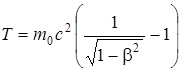. (4)

Подставив числовые данные, выраженные в единицах СИ, найдем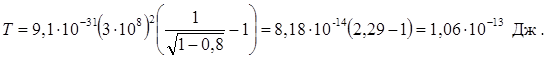

Во внесистемных единицах энергия покоя электрона m₀ с² = 0,51 МэВ. Подставив это значение в формулу (4), получим Т = 0,51∙1,29 = 0,66 МэВ.

№ 8.Определить релятивистский импульс электрона, обладающего кинетической энергией Т = 5 МэВ.

Р е ш е н и е.

Релятивистский импульс электрона определяется по формуле (см. пример 7) 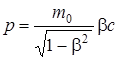, но так как в условии задачи дана не скорость электрона, а его кинетическая энергия, то решение задачи в общем виде сводится к отысканию формулы, выражающей импульс непосредственно через кинетическую энергию.

Установим связь между релятивистским импульсом и полной энергией частицы. Полная энергия Е частицы прямо пропорциональна ее массе, т.е.

Е = mc². (1)

Зависимость массы от скорости определяется формулой

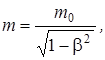(2)

Заменив массу m в формуле (1) ее выражением (2) и приняв во внимание, что произведение m₀с²есть энергия Е₀ частицы, получим

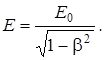(3)

Возведя обе части равенства (3) в квадрат, найдем 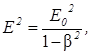откуда

Е² - (βЕ)² = Е₀² . (4)

Очевидно, что βЕ = (v/c)∙ mc² = mvc = pc. Поэтому равенство (4) можно переписать в виде Е² – р²с² = Е₀², откуда релятивистский импульс .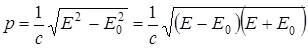

Разность между полной энергией и энергией покоя есть кинетическая энергия Т частицы: Е – Е₀ = Т.

Легко убедиться, что Е + Е₀ = Т + 2Е₀, поэтому искомая связь между импульсом и кинетической энергией релятивистской частицы выразится формулой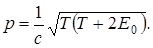

Вычисления удобно провести в два приема: сначала найти числовое значение радикала во внесистемных единицах, а затем перейти к вычислению в единицах СИ. Таким образом,

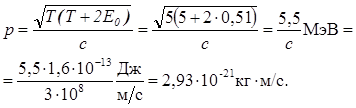
№ 9.Длина волны, на которую приходится максимум энергии в спектре излучения абсолютно черного тела, λ₀ = 0,58 мкм. Определить энергетическую светимость (излучательность) R₀ поверхности тела.

Ре ш е н и е.

Энергетическая светимость R₀ абсолютно черного тела в соответствии с законом Стефана - Больцмана пропорциональна четвертой степени абсолютной температуры и выражается формулой

R₀ = σТ⁴, (1)

где σ - постоянная Стефана – Больцмана; Т – термодинамическая температура.

Температуру Т можно вычислить с помощью закона смещения Вина

λ₀ = b/Т. (2)

где b - постоянная закона смещения Вина.

Используя формулы (2) и (1), получим

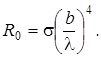(3)

Выпишем числовые значения величин, входящих в эту формулу

σ = 5,67×10^-8 Вт/(м²∙К⁴), b = 2,90∙10^-3 м∙К, λ₀ = 5,8×10^-7 м, и подставив числовые значения в формулу (3), произведем вычисления:

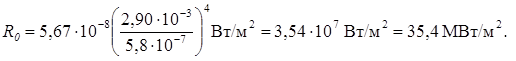
№ 10. Определить максимальную скорость v_max фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиоле­товыми лучами с длиной волны λ₁ = 0,155 мкм; 2) γ - лучами с длиной волны λ₂ = 1 пм.

Р е ш е н и е.

Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фотоэффекта

ε = А + Т_max, (1)

где ε - энергия фотона, падающего на поверхность металла; А - работа выхода электрона из металла; Т_max - максимальная кинетическая энергия фотоэлектрона.

Энергия фотона вычисляется также по формуле

ε = hс/λ, (2)

где h - постоянная Планка; с - скорость света в вакууме; λ - длина волны.

Кинетическая анергия электрона может быть выражена или по классической формуле

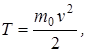(3)

или по релятивистской

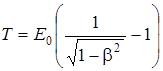(4)

в зависимости от того, какая скорость сообщается фотоэлектрону.

Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия ε фотона много меньше энергии покоя Е₀ электрона, то может быть применена формула (3), если же ε сравнима по величине с Е₀, то вычисление по формуле (3) приводит к ошибке, поэтому нужно пользоваться формулой (4).

1. Вычислим энергию фотона ультрафиолетовых лучей по формуле (2):

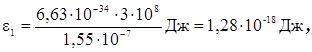или .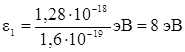

Полученная энергия фотона (8 эВ) много меньше энергии покоя электрона (0,51 МэВ). Следовательно, для данного случая кинетическая энергия фотоэлектрона в формуле (1) может быть выражена по классической формуле (3): ε₁ = А + 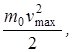откуда

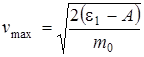. (5)

Выпишем числовые значения величин: ε₁ = 1,28 10^-18 Дж (вычислено выше), А = 4,7 эВ = 4,7 ∙ 1,6 10^-19 Дж, m₀ = 9,11 10^-31 кг.

Подставив числовые значения в формулу (5), найдем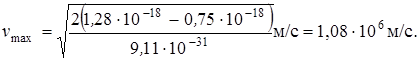

2. Вычислим энергию фотона γ – лучей: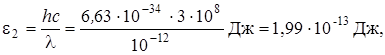

или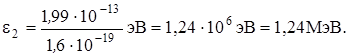

Работа выхода электрона (А = 4,7 эВ) пренебрежимо мала по сравнению с энергией фотона (ε₂ = 1,24 МэВ), поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона: Т_max = ε₂ = 1,24 МэВ. Так как в данном случае кинетическая энергия электрона больше его энергии покоя, то для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии (4). Из этой формулы найдем 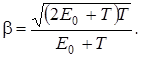Заметив, что v = cβ и Т _max = ε₂, получим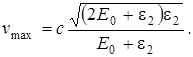

Подставим числовые значения величин и произведем вычисления:

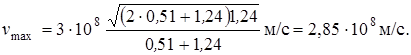
№ 11.В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол θ = 90⁰. Энергия рассеянного фотона ε₂ = 0,4 МэВ. Определить энергию фотона ε₁ до рассеяния.

Р е ш е н и е.

Для определения энергии первичного фотона воспользуемся формулой Комптона

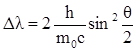, (1)

где Δλ = λ₂ - λ₁ - изменение длины волны фотона в результате рассеяния на свободном электроне; h - постоянная Планка; m₀ - масса покоя электрона; с - скорость света в вакууме; θ - угол рассеяния фотона.

Формулу (1) преобразуем следующим образом: 1) заменим в ней Δλ на λ₂ - λ₁; 2) выразим длины волн λ₁ и λ₂ через энергии ε₁ и ε₂ соответствующих фотонов, воспользовавшись формулой ε = hc/λ; 3) ум­ножим числитель и знаменатель правой части формулы на с. Тогда получим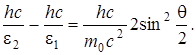

Сократим на hс и выразим из полученной формулы искомую энергию:

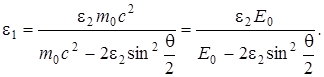(2)

где Е₀ = mc² - энергия покоя электрона.

Вычисления по формуле (2) удобно вести во внесистемных единицах. Взяв из таблицы значение энергии покоя электрона в мегаэлектрон-вольтах и подставив числовые данные, получим .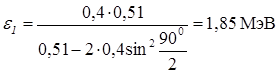

№ 12.Пучок параллельных лучей монохроматического света с длиной волны λ = 663 нм падает нормально на плоскую зеркальную поверхность. Поток излучения Ф = 0,6 Вт. Определить: 1) силу F давления, испытываемую этой поверхностью; 2) число N₁ фотонов, ежесекундно падающих на поверхность.

Р е ш е н и е.

1. Сила светового давления на поверхность равна произведению светового давления р на площадь S поверхности:

F = рS. (1)

Световое давление может быть найдено по формуле

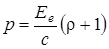, (2)

где Е_e - энергетическая освещенность (облученность); c - скорость света в вакууме; ρ - коэффициент отражения.Подставляя выражение (2) давления света в формулу (1), получим

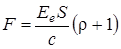. (3)

Энергетическая освещенность Е_еесть величина, численно равная энергии, падающей на единичную площадку в единицу времени. Произведение Е_е на S есть величина, численно равная энергии, падающей на данную площадку S в единицу времени, т.е. поток излучения Ф = Е_еS. С учетом этого формула (3) примет вид

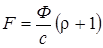. (4)

Величины, входящие в формулу (4), выпишем в единицах СИ: Ф = 0,6 Вт, с = 3-10⁸ м/с, ρ = 1 (поверхность зеркальная). После подстановки этих величин в формулу (4) получим .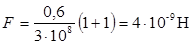

2. Произведение энергии ε одного фотона на число фотонов N₁, падающих на поверхность в единицу времени, равно мощности излучения, т.е. потоку излучения: Ф = εN₁, а так как, энергия фотона ε = hc/λ, то

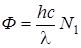, откуда

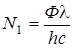. (5)

Выпишем величины, входящие в формулу (5), в единицах СИ: Ф = 0,6 Вт, λ = 6,63×10^-7м, h = 6,63×10^-34 Дж∙с, с = 3×10⁸ м/с. Подставим полученные значения в расчетную формулу и произведем вычисления: .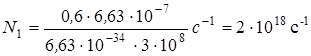

ТРЕНИРОВОЧНЫЕ ЗАДАЧИ

1. На мыльную пленку с показателем преломления n = 1,33 падает по нормали монохроматический свет с длиной волны λ = 0,6 мкм. Отраженный свет в результате интерференции имеет наибольшую яркость. Какова возможная наименьшая толщина d_min пленки? (Ответ. 0,113 мкм).

2. Радиус второго темного кольца Ньютона в отраженном свете r₂ = 0,4 мм. Определить радиус R кривизны плосковыпуклой линзы, взятой для опыта, если она освещается монохроматическим светом с длиной волны λ = 0,64 мкм. (Ответ. 125 мм).

3. На пластинку со щелью, ширина которой а = 0,05 мм, падает нормально монохроматический свет с длиной волны λ = 0,7 мкм. Определить угол φ отклонения лучей, соответствующих первому дифракционному максимуму. (Ответ. 1⁰12^/).

4. Дифракционная решетка, освещенная нормально падающим монохроматическим светом, отклоняет спектр третьего порядка на угол φ₁ = 30⁰. На какой угол φ₂ отклоняет она спектр четвертого порядка? (Ответ. 41⁰50¢).

5. Угол преломления луча в жидкости i₂ = 35⁰. Определить показатель n преломления жидкости, если известно, что отраженный луч максимально поляризован. (Ответ. 1,43).

6. На сколько процентов уменьшается интенсивность света после прохождения через призму Николя, если потери света составляют 10%? (Ответ. 55%).

7. При какой скорости v релятивистская масса частицы в к = 3 раза больше массы покоя этой частицы? (Ответ. 2,83×10⁸ м/с).

8. Определить скорость v электрона, имеющего кинетическую энергию Т = 1,53 МэВ. (Ответ 2,91×10⁸ м/с).

9. Электрон движется со скоростью v = 0,6 c, где с – скорость света в вакууме. Определить релятивистский импульс р электрона. (Ответ.2,0×10^-22 кг×м/c).

10. Вычислить энергию, излучаемую за время t = 1 мин с площади S = 1 см² абсолютно черного тела, температура которого Т = 1000 К. (Ответ. 340 Дж).

11. Длина волны, на которую приходится максимум энергии излучения абсолютно черного тела, λ₀ = 0,6 мкм. Определить температуру Т тела. (Ответ. 4820 К).

12. Определить спектральную плотность r_λ энергетической светимости (излучательности), рассчитанную на 1 нм для λ₀ в спектре излучения абсолютно черного тела. Температура тела Т = 1 К. (Ответ. 13 Вт/(м² нм).

13. Определить энергию ε, массу m и импульс р фотона с длиной волны λ = 1,24 нм. (Ответ. 1,60×10^-16 Дж; 1,78×10^-33 кг; 5,33×10^-25 кг×м/с).

14. На пластину падает монохроматический свет (λ = 0,42 мкм). Фототок прекращается при задерживающей разности потенциалов U = 0,95 В. Определить работу А выхода электронов с поверхности пластины. (Ответ. 2 эВ).

15. На цинковую пластинку падает пучок ультрафиолетовых лучей (λ = 0,2 мкм). Определить максимальную кинетическую энергию Т_max и максимальную скорость v_max фотоэлектронов. (Ответ. 2,2 эВ, 8,8×10⁵ м/с).

16. Определить максимальную скорость v_max фотоэлектрона, вырванного с поверхности металла γ-квантом с энергией ε = 1,53 МэВ. (Ответ. 2,91×10⁸ м/с).

17. Фотон с энергией ε₁, равной энергии покоя электрона (m₀c²), рассеялся на свободном электроне на угол θ = 120⁰. Определить энергию ε₂ рассеянного фотона и кинетическую энергию Т электрона отдачи (в единицах m₀c²). (Ответ. 0,4 m₀c²; 0,6 m₀c²).

18. Поток энергии (излучается электрической лампой) Ф₀ = 600 Вт. На расстоянии r = 1м от лампы перпендикулярно падающим лучам расположено круглое плоское зеркальце диаметром d = 2 см. Определить силу F светового давления на зеркальце. Лампу рассматривать как точечный изотропный излучатель. (Ответ. 0,1 нН.).