Атом водорода в теории Бора

• Момент импульса электрона на стационарных орбитах

L=mvr = nħ (n=1,2,3,…),

где т — масса электрона; r — радиус орбиты; v — скорость элект­рона на орбите; п — главное квантовое число; ħ — постоянная Планка.

• Энергия электрона, находящегося на n-й орбите,

,

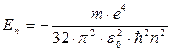где ε₀ — электрическая постоянная.

• Сериальная формула, определяющая длину волны λ или ча­стоту υ света, излучаемого или поглощаемого атомом водорода при переходе из одного стационарного состояния в другое,

, ,

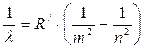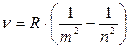где R' и R —постоянная Ридберга (R'=1,097∙10⁷ м^-1; R=c∙R'=3,29∙10¹⁵ с^-1); m и m — целые числа; n — номер серии спект­ральных линий (n=l — серия Лаймана, n=2 — серия Бальмера, n=3 — серия Пашена и т. д.). Для данной серии n=m+l, m+ 2, m+3 и т. д.

• Энергия фотона, испускаемого атомом водорода при переходе из одного

стационарного состояния в другое,

,

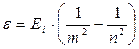где E_i — энергия ионизации водорода: E_i=2πhħR=13,6 эВ.

Волновые свойства микрочастиц

· Формула де Бройля, выражающая связь длины волн с импуль­сом р движущейся частицы, для двух случаев:

а) в классическом приближении (n<<c; p= m₀n)

l = 2pħ/p

б) в релятивистском случае (скорость и частицы сравнима со скоростью с света в вакууме;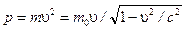

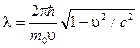
· Связь длины волны де Бройля с кинетической энергией Т частицы:

а) в классическом приближении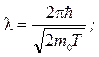

б) в релятивистском случае 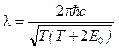, где E₀ — энергия покоя частицы.

· Фазовая скорость волн де Бройля

n = w/k

где w — круговая частота; k — волновое число (k = 2p/l).

· Групповая скорость волн де Бройля

.

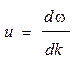· Соотношения де Бройля:

E=ħw, p = ħk,

где Е — энергия движущейся частицы; р — импульс частицы; k — волновой вектор;

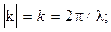ħ - постоянная Планка (ħ =h/(2p) =1,05.10^-34 Дж.с).

· Соотношения неопределенностей:

а) для координаты и импульса частицы DpDx≥ħ где Dp_x — неопределенность проекции импульса частицы на ось х; Dx — неоп­ределенность ее координаты;

б) для энергии и времени DEDt≥ħ, где DE — неопределенность энергии данного квантового состояния; Dt — время пребывания системы в этом состоянии.

Радиоактивность

• Основной закон радиоактивного распада

N=N₀e^-λt,

где N — число нераспавшихся атомов в момент времени t; N₀— число нераспавшихся атомов в момент, принятый за начальный (при t=0); е — основание натуральных логарифмов; λ — постоян­ная радиоактивного распада.

• Период полураспада T_1/2 — промежуток времени, за который число нераспавшихся атомов уменьшается в два раза. Период полу­распада связан с постоянной распада соотношением

T_1/2 = ln2/λ = 0,693/λ .

• Число атомов, распавшихся за время t,

∆N = N₀ - N = N₀, (1 - е^-λt).

Если промежуток времени ∆t << T_1/2. то для определения числа распавшихся атомов можно применять приближенную формулу

∆N ≈ λN∆t

Среднее время жизни т радиоактивного ядра — промежуток времени, за который число нераспавшихся ядер уменьшается в е раз:

τ = 1/λ

• Число атомов, содержащихся в радиоактивном изотопе,

N = (m/M)×N_A

где m — масса изотопа; М — его молярная масса; N_A — постоян­ная Авогадро.

• Активность А нуклида в радиоактивном источнике (актив­ность изотопа) есть величина, равная отношению числа dN ядер, распавшихся в изотопе, к промежутку времени dt, за которое произошел распад. Активность определяется по формуле

A = -dN/dt = λN,

или после замены N по основному закону радиоактивного распада

A = λN₀e^-λt

Активность изотопа в начальный момент времени (t=0)

A₀ = λN₀ .

Активность изотопа изменяется со временем по тому же закону, что и число нераспавшихся ядер:

A = A₀e^-λt

• Массовая активность а радиоактивного источника есть величина равная отношению его активности A к массе т этого источни­ка, т. е.

a = A/m.

● Если имеется смесь ряда радиоактивных изотопов, образую­щихся один из другого, и если постоянная распада λ первого члена ряда много меньше постоянных всех остальных членов ряда, то в смеси устанавливается состояние радиоактивного равновесия, при котором активности всех членов ряда равны между собой:

λ₁N₁ = λ₂N₂ = … = λ_kN_k..

Примеры решения задач

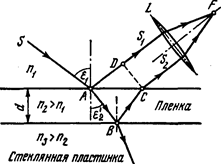Пример 1. На толстую стек­лянную пластинку, покрытую очень тонкой пленкой, показа­тель преломления n₂ вещества которой равен 1,4, падает нор­мально параллельный пучок монохроматического света (λ=0,6 мкм). Отраженный свет максимально ослаблен вследст­вие интерференции. Определить толщину d пленки.

Рис. 2

Решение. Из световой волны, падающей на пленку, выделим узкий пучок SA. Ход этого пучка в случае, когда угол падения ε₁ 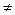0, показан на рис. 2. В точках A и В падающий пучок частич­но отражается и частично преломляется. Отраженные пучки света AS₁ и BCS₁ падают на собирающую линзу L, пересекаются в ее фокусе F и интерферируют между собой.

Так как показатель преломления воздуха (n₁= 1,00029) меньше показателя преломления вещества пленки (n₂=1,4), который, в свою очередь, меньше показателя преломления стекла (n₃=1,5), то в обоих случаях отражение происходит от среды оптически более плотной, чем та среда, в которой идет падающая волна. Поэтому фаза колебания пучка света AS₁ при отражении в точке A изменя­ется на π рад и точно так же на π рад изменяется фаза колебаний пучка света BCS₂ при отражении в точке В. Следовательно, резуль­тат интерференции этих пучков света при пересечении в фокусе F линзы будет такой же, как если бы никакого изменения фазы коле­баний ни у того, ни у другого пучка не было.

Как известно, условие максимального ослабления света при интерференции в тонких пленках состоит в том, что оптическая раз­ность хода Δ интерферирующих волн должна быть равна нечетному числу полуволн; Δ=(2k+1)(λ/2).

Как видно из рис. 2, оптическая разность хода

Δ=l₂n₂— l₁n₁=(|АВ| +|ВС|) п₂—|AD| n₁.

Следовательно, условие минимума интенсивность света примет вид

(|АВ| +|ВС|) п₂—|AD| n₁=(2k+1)(λ/2).

Если угол падения ε₁ будет уменьшаться, стремясь к нулю, то AD 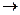0 и (|АВ|+|ВС| 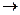2d, где d—толщина пленки. В пределе при ε₁=0 будем иметь

Δ=2dn₂=(2k+1)(λ /2),

откуда искомая толщина пленки

.

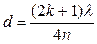Полагая k=0,1,2,3,…, получим ряд возможных значений толщины пленки:

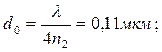
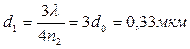и т.д.

Пример 2. На стеклянный клин нормально к его грани падает монохроматический свет с длиной волны λ=0,6 мкм. В возникшей при этом интерференционной картине на отрезке длиной l=1 см наблюдается 10 полос. Определить преломляющий угол θ клина.

Решение. Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней грани. Эти пучки когерентны, и поэтому наблюдается устойчивая картина интерференции. Так как интерференционные полосы наблюдаются при малых углах клина, то отраженные пучки света 1 и 2 (рис. 3) будут практически параллельны.

Темные полосы видны на тех участках клина, для которых раз­ность хода кратна нечетному числу половины длины волны;

Δ=(2k+1) (λ/2), где k=0,1,2,…. (1)

Разность хода Δ двух волн складывается из разности оптических длин путей этих волн (2dn cosε₂’) и половины длины волны (λ/2).

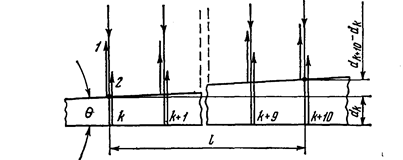
Рис. 3

Величина λ/2 представляет собой добавочную разность хода, воз­никающую при отражении волны от оптически более плотной среды. Подставляя в формулу (1) значение разности хода Δ, получим

2d_kn cos ε₂’ + λ/2 = (2k + 1) (λ/2), (2)

где п — коэффициент преломления стекла (n=l,5); d_k—толщина клина в том месте, где наблюдается темная полоса, соответствую­щая номеру k; ε₂’—угол преломления.

Согласно условию, угол падения равен нулю, следовательно, и угол преломления ε₂’ равен нулю, a cos ε₂’=1. Раскрыв скобки в правой части равенства (2), после упрощения получим

2d_kn=kλ (3)

Пусть произвольной темной полосе номера k соответствует опре­деленная толщина клина в этом месте d_k а темной полосе номера k+10 соответствует толщина клина d_k+10. Согласно условию за­дачи, 10 полос укладываются на отрезке длиной l=1 см. Тогда ис­комый угол (рис. 3) будет равен

θ=(d_k+10 – d_k)/l, (4)

где из-за малости преломляющего угла sin θ=θ (угол θ выражен в радианах).

Вычислив d_k и d_k+10 из формулы (3), подставив их в формулу (4) и произведя преобразования, найдем

θ=5λ/(nl).

После вычисления получим

θ=2∙10^-4paд.

Выразим θ в градусах. Для этого воспользуемся соотношением между радианом и секундой (см. табл. 6); 1 рад=2,06"∙10⁵, т. е.

θ=2∙10^-4∙2,06''∙10⁵=41,2'',

или в соответствии с общим правилом перевода из радиан в градусы

θ_град = 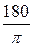θ_рад, θ= .

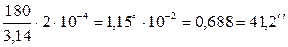Искомый угол равен 41,2".

Пример 3. На диафрагму с круглым отверстием радиусом r=1 мм падает нормально параллельный пучок света длиной волны λ=0,05 мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние b_max от центра от­верстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пят­но.

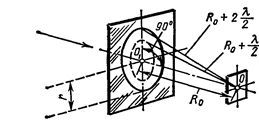Решение. Расстояние, при котором будет видно темное пят­но, определяется числом зон Фре­неля, укладывающихся в отвер­стии. Если число зон четное, то в центре дифракционной картины бу­дет темное пятно.

Число зон Френеля, помещаю­щихся в отверстии, убывает по мере удаления экрана от отверстия. Наименьшее четное число зон равно двум. Следовательно, максимальное расстояние, при котором еще будет наблюдаться темное пятно Рис. 4 в центре экрана, определяется условием, согласно которому в отверстии должны поместиться две зоны Френеля.

Из рис. 4 следует, что расстояние от точки наблюдения O на экране до края отверстия на 2 (λ/2) больше, чем расстояние b_max.

По теореме Пифагора получим

.

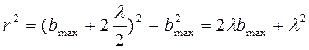Учтя, что λ<<b_mах и что членом, содержащим λ², можно пренеб­речь, последнее равенство перепишем в виде

r²=2λb_max. откуда b_max=r²/(2λ). Произведя вычисления по последней формуле, найдем

b_max=1 м.

Пример 4. На щель шириной а=0,1 мм нормально падает параллельный пучок света от монохроматического источника (λ==0,6 мкм). Определить ширину l центрального максимума в дифракционной картине, проецируемой с помощью линзы, нахо­дящейся непосредственно за щелью, на экран, отстоящий от лин­зы на расстоянии L=l м.

Решение. Центральный максимум интенсивности света за­нимает область между ближайшими от него справа и слева миниму­мами интенсивности. Поэтому ширину центрального максимума интенсивности примем равной расстоянию между этими двумя минимумами интенсивности (рис. 5).

Минимумы интенсивности света при дифракции от одной щели наблюдаются под углами φ, определяемыми условием

a sin φ=±kλ, (1)

где k — порядок минимума; в нашем случае равен единице.

Расстояние между двумя минимумами на экране определим не­посредственно по чертежу: l=2L tgφ. Заметив, что при малых уг­лах tg φ 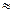sin φ, перепишем эту формулу в виде

Рис. 5

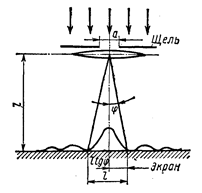l=2L sin φ. (2)

Выразим sin φ из формулы (1) и подставим его в равенство (2):

l=2Lkλ/a. (3)

Произведя вычисления по фор­муле (3), получим l=1,2 см.

Пример 5. На дифракционную решетку нормально к ее поверх­ности падает параллельный пучок света с длиной волны λ=0,5мкм. Помещенная вблизи решетки лин­за проецирует дифракционную картину на плоский экран, удаленный от линзы на L=l м. Расстоя­ние l между двумя максимумами интенсивности первого порядка, наблюдаемыми на экране, равно 20,2 см (рис. 6). Определить: 1) постоянную d дифракционной решетки; 2) число n штрихов на 1 см; 3) число максимумов, которое при этом дает дифракционная решетка; 4) максимальный угол φ_mах отклонения лучей, соот­ветствующих последнему дифракционному максимуму.

Решение1. Постоянная d дифракционной решетки, длина волны λ и угол φ отклоне­ния лучей, соответствую­щий k-му дифракционному максимуму, связаны соот­ношением

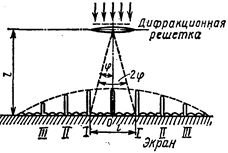dsin φ=kλ, (1)

где k — порядок спектра, или в случае монохрома­тического света порядок максимума.

В данном случае k=1, sin φ=tg φ (ввиду того, что l/2<<L), tgφ=(l/2)L (следует из рис. 31.3). С учетом последних трех равенств соотношение (1) примет вид

Рис. 6 ,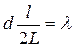

откуда постоянная решетки

d=2Lλ/l.

Подставляя данные, получим

d=4,95 мкм.

2. Число штрихов на 1 см найдем из формулы

п=1/d.

После подстановки числовых значений получим n=2,02-10³ см^-1.

3. Для определения числа максимумов, даваемых дифракцион­ной решеткой, вычислим сначала максимальное значение k_max исходя из того, что максимальный угол отклонения лучей решеткой не может превышать 90°.

Из формулы (1) запишем

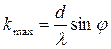. (2)

Подставляя сюда значения величин, получим

K_max =9,9.

Число k обязательно должно быть целым. В то же время оно не может принять значение, равное 10, так как при этом значении sin φ должен быть больше единицы, что невозможно. Следователь­но, k_mах=9.

Определим общее число максимумов дифракционной картины, полученной посредством дифракционной решетки. Влево и вправо от центрального максимума будет наблюдаться по одинаковому числу максимумов, равному k_mах, т. е. всего 2k_mах. Если учесть также центральный нулевой максимум, получим общее число мак­симумов

N=2k_max+l.

Подставляя значение k_mах найдем

N=2∙9+1=19.

4. Для определения максимального угла отклонения лучей, соответствующего последнему дифракционному максимуму, выра­зим из соотношения (2) синус этого угла:

sinφ_max=k_maxλ/d.

Отсюда

φ_max=arcsin(k_maxλ/d).

Подставив сюда значения величин λ, d, k_mах и произведя вычис­ления, получим

φ_mах=65,4°.

Пример 6. Исследование спектра излучения Солнца показы­вает, что максимум спектральной плотности энергетической све­тимости соответствует длине волны λ=500 нм Принимая Солнце за черное тело, определить. 1) энергетическую светимость Me Солнца;

2) поток энергииФ_е, излучаемый Солнцем; 3) массу т электромаг­нитных волн (всех длин), излучаемых Солнцем за 1 с.

Решение: 1. Энергетическая светимость M_e черного тела выражается формулой Стефана — Больцмана

R_e=sT⁴ (1)

Температура излучающей поверхности может быть определена из закона смещения Вина. λ_m=b/T. Выразив отсюда температуру Т и подставив ее в формулу (1), получим

R_e=s (bλ_m)⁴, (2)

Произведя вычисления по формуле (2), найдем

R_e =64 МВт/м².

2. Поток энергии Ф_е, излучаемый Солнцем, равен произведению энергетической светимости Солнца на площадь S его поверхности.

Ф_е = 4πr²R_e , (3)

где r — радиус Солнца

Подставив в формулу (3) значения π, r и R_e и произведя вычис­ления, получим

Ф_е =3,9∙10²⁶ Вт.

3. Массу электромагнитных волн (всех длин), излучаемых Солн­цем за время t=1 с, определим, применив закон пропорциональ­ности массы и энергии Е=тс². Энергия электромагнитных волн, излучаемых за время t, равна произведению потока энергии Ф (мощ­ности излучения) на время Е=Фt. Следовательно, Ф_е = тс², откуда т= Ф_е /с²

Произведя вычисления по этой формуле, найдем

m = 4,3∙10⁹ кг.

Пример 7. Длина волны λ_m , на которую приходится максимум энергии в спектре излучения черного тела, равна 0,58 мкм. Опре­делить максимальную спектральную плотность энергетической светимости (r_λ,T)_max , рассчитанную на интервал длин волн ∆λ=1нм, вблизи λ_m.

Решение. Максимальная спектральная плотность энергети­ческой светимости пропорциональна пятой степени температуры Кельвина и выражается формулой

(r_λ,T)_max = СТ⁵. (1)

Температуру Т выразим из закона смещения Вина λ_m =b/Т, откуда Т=b/λ_т

Подставив полученное выражение температуры в формулу (1), найдем

(r_λ,T)_max=C(b/λ_m)⁵,

В табл. 24 значение С дано в единицах СИ, в которых единичный интервал длин волн ∆λ=1 м. По условию же задачи требуется вы­числить спектральную плотность энергетической светимости, рас­считанную на интервал длин волн 1 нм, поэтому выпишем значение С в единицах СИ и пересчитаем его на заданный интервал длин волн:

С=1,30∙10^-5 Вт/(м³К⁵)=1,30∙10^-5 Вт/(м²∙м∙K⁵) =

=1,30∙10^-14 Вт/(м²∙нм∙К⁵).

Вычисление по формуле (2) дает

(r_λ,T)_max=40,6 кВт/(м∙нм).

Пример 8. Определить максимальную скорость v_max фотоэлект­ронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны λ₁ =0,155 мкм; 2) γ-излучением с длиной волны λ₂=2,47 пм.

Решение. Максимальную скорость фотоэлектронов опреде­лим из уравнения Эйнштейна для фотоэффекта:

ε =A+T_max (1)

Энергия фотона вычисляется по формуле ε = hc/λ , работа выхода для серебра A =4,7 эВ.

Кинетическая энергия фотоэлектрона в зависимости от того, ка­кая скорость ему сообщается, может быть выражена или по класси­ческой формуле

T= ½ m₀v² (2)

или по релятивистской

Т = (m—m₀)c² (3)

Скорость фотоэлектрона зависит от энергии фотона, вызывающе­го фотоэффект: если энергия фотона ε много меньше энергии покоя электрона Е₀ , то может быть применена формула (2); если же ε сравнима по размеру с Е₀ , то вычисление по формуле (2) приводит к грубой ошибке, в этом случае кинетическую энергию фотоэлектрона необходимо выражать по формуле (3)

1. В формулу энергии фотона ε = hc/λ подставим значения вели­чин h, с и λ и, произведя вычисления, для ультрафиолетового излу­чения получим

ε₁ = 8 эВ.

Это значение энергии фотона много меньше энергии покоя элек­трона (0,51 МэВ). Следовательно, для данного случая максимальная кинетическая энергия фотоэлектрона в формуле (1) может быть вы­ражена

по классической формуле (2) ε₁=A+ ½ m₀v²_max , откуда

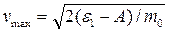(4)

Выпишем величины, входящие в формулу (4): ε₁=1,28×10^-18 Дж (вычислено выше); A=4,7 эВ = 4,7×1,6∙10^-19 Дж = 0,75∙10^-18 Дж; m₀=9,11×10^{-31 кг}.

Подставив числовые значения в формулу (4), найдем максималь­ную скорость:

v_max =1,08 Мм/с.

2. Вычислим теперь энергию фотона γ-излучения:

ε₂=hc/λ₂ = 8,04 фДж = 0,502 МэВ.

Работа выхода электрона (A = 4,7 эВ) пренебрежимо мала по сравнению с энергией γ-фотона, поэтому можно принять, что макси­мальная кинетическая энергия электрона равна энергии фотона:

T_max = ε₂=0,502 МэВ.

Так как в данном случае кинетическая энергия электрона сравни­ма с его энергией покоя, то для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии,

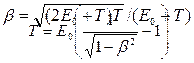где E₀=m₀c².

Выполнив преобразования, найдем

Сделав вычисления, получим

β = 0,755.

Следовательно, максимальная скорость фотоэлектронов, вырывае­мых γ-излучением,

v_max=cβ=226 Mм/c.

Пример 9. Определить красную границу λ₀ фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом длиной волны λ=400 нм максимальная скорость v_max фотоэлектро­нов равна 0,65 Мм/с.

Решение. При облучении светом, длина волны λ₀ которого соответствует красной границе фотоэффекта, скорость, а следова­тельно, и кинетическая энергия фотоэлектронов равны нулю. Поэтому уравнение Эйнштейна для фотоэффекта ε =A+T в случае красной границы запишется в виде

ε = A, или hc/ λ₀=A.

Отсюда

λ₀ =hc/A . (1)

Работу выхода для цезия определим с помощью уравнения Эйн­штейна:

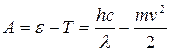
(2)

Выпишем числовые значения величин, выразив их в СИ: h=6,62∙10^-34 Дж∙с; с = 3∙10⁸ м/с; λ=400 нм=4∙10^{-7 м;} m=9,11∙10^{-31 кг;} v = 6,5∙10⁵ м/с.

Подставив эти значения величин в формулу (2) и вычислив, полу­чим

A=3,05×10^-19 Дж = 1,9 эВ.

Для определения красной границы фотоэффекта подставим значения A, h и с в формулу (1) и вычислим:

λ₀=651 нм.

Пример 10. Пучок монохроматического света с длиной волны λ = 663 нм падает нормально на зеркальную плоскую поверхность Поток энергии Ф_е=0,6 Вт. Определить силу F давления, испытывае­мую этой поверхностью, а также число N фотонов, падающих на нее за время t=5 с

Решение Сила светового давления на поверхность равна произведению светового давления р на площадь S поверхности:

F=pS. (1)

Световое давление может быть найдено по формуле

P=E_e(ρ+l)/c. (2)

Подставляя выражение (2) дaвлeния света в формулу (1), получим

F= [(E_eS)/c]∙(ρ+1). (3)

Так как произведение облученности E_e на площадь S поверх­ности равно потоку Ф энергии излучения, падающего на поверх­ность, то соотношение (3) можно записать в виде

F = (Ф_е/с)∙(ρ+1).

После подстановки значений Ф_е и с с учетом, что ρ=1 (поверх­ность зеркальная), получим

F==4 нН.

Число N фотонов, падающих за время ∆t на поверхность, опре­деляется по формуле

N=∆W/ε = Ф_е ∆t/ε ,

где ∆W — энергия излучения, получаемая поверхностью за время ∆t

Выразив в этой формуле энергию фотона через длину волны (ε =hc/λ), получим

N= Ф_еλ∆t/(hc).

Подставив в этой формуле числовые значения величин, найдем

N=10¹⁹ фотонов.

Пример 11. Параллельный пучок света длиной волны λ=500 нм падает нормально на зачерненную поверхность, производя давление p=10 мкПа. Определить: 1) концентрацию п фотонов в пучке, 2) число n₁ фотонов, падающих на поверхность площадью 1 м² за вре­мя 1 с.

Решение.1. Концентрация п фотонов в пучке может быть найдена, как частное от деления объемной плотности энергии w на энергию ε одного фотона:

n=w/ε (1)

Из формулы p=w(1+ρ), определяющей давление света, где ρ-коэффициент отражения, найдем

w = p/(ρ+1). (2)

Подставив выражение для w из уравнения (2) в формулу (1), получим

n = ρ/[(ρ+1)∙ε]. (3)

Энергия фотона зависит от частоты υ, а следовательно, и от длины световой волны λ:

ε = hυ = hc/λ (4)

Подставив выражение для энергии фотона в формулу (3), опре­делим искомую концентрацию фотонов:

n = (ρλ)/[(ρ+1)∙ε]. (5)

Коэффициент отражения ρ для зачерненной поверхности прини­маем равным нулю.

Подставив числовые значения в формулу (5), получим

n=2,52∙10¹³ м^-3.

2. Число n₁ фотонов, падающих на поверхность площадью 1 м² за время 1 с, найдем из соотношения n₁=N/(St), где N — число фо­тонов, падающих за время t на поверхность площадью S. Но N=ncSt, следовательно,

n₁=(ncSt)/(St)=nc

Подставив сюда значения п и с, получим

n₁=7,56∙10²¹ м^-2∙с^-1.

Пример 12. В результате эффекта Комптона фотон при соударе­нии с электроном был рассеян на угол θ=90°. Энергия ε' рассеянного фотона равна 0,4 МэВ. Определить энергию ε фотона до рассеяния.

Решение. Для определения первичного фотона воспользу­емся формулой Комптона в виде

λ`-λ = 2×[(2πħ)/(mc)]×sin²(θ/2). (1)

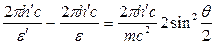Формулу (1) преобразуем следующим образом: 1) выразим длины волн λ' и λ через энергии ε' и ε соответствующих фотонов, восполь­зовавшись соотношением ε = 2πħc/λ; 2) умножим числитель и зна­менатель правой части формулы на с. Тогда получим

Сократив на 2nħc, выразим из этой формулы искомую энергию:

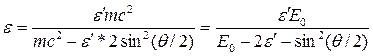
ε = 1,85 МэВ.

Пример 13. Фотон с энергией ε =0,75 МэВ рассеялся на свобод­ном электроне под углом θ=60°. Принимая, что кинетическая энер­гия и импульс электрона до соударения с фотоном были пренебре­жимо малы, определить: 1) энергию ε' рассеянного фотона; 2) кинетическую энергию Т электрона отдачи; 3) направление его движения.

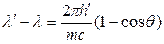Решение. 1. Энергию рассеянного фотона найдем, восполь­зовавшись формулой Комптона:

Выразив длины волн λ' и λ через энергии ε' и ε соответствующих фотонов, получим

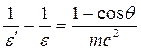
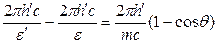
(1)

Разделим обе части этого равенства на 2πħc:

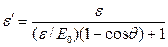От­сюда, обозначив для краткости энергию покоя электрона тc² через е_о, найдем

Подставив числовые значения величин, получим

ε'=0,43 МэВ.

2. Кинетическая энергия электрона отдачи, как это следует из закона сохранения энергии, равна разности между энергией ε па­дающего фотона и энергией е' рассеянного фотона:

T = ε - ε` = 0,32 МэВ.

3. Направление движения электрона отдачи найдем, применив закон сохранения импульса, согласно которому импульс падающего фотона р равен векторной сумме импульсов рассеянного фотона р' и электрона отдачи mv:

p = p'+mv.

Векторная диаграмма импульсов изображена на рис.. Все векторы проведены из точки О, где находился электрон в момент соударения с фотоном. Угол φ определяет направление движения электрона отдачи.

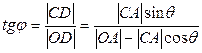Из треугольника OCD находим

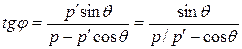или

Так как р=ε/с и р'=е'/с, то

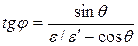
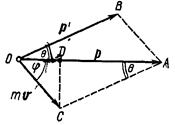(2)

Рис. 7

Преобразуем формулу (2) так, чтобы угол φ выражался непосредственно через величины ε и θ, за­данные в условии задачи. Отсюда

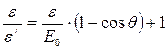(3)

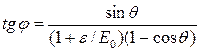Заменим в формуле (2) соотношение ε/ε' по формуле (3):

Учитывая, что sin θ=2sin(θ/2)cos(θ/2) и 1—cosθ=2sin²(θ/2), после соответствующих преобразований получим

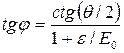(4)

После вычисления по формуле (4) найдем tg φ =0,701, откуда φ=35°.

Пример 14. Вычислить радиус первой орбиты атома водорода (Боровский радиус) и скорость электрона на этой орбите.

Решение. Согласно теории Бора, радиус r электронной ор­биты и скорость v электрона на ней связаны равенством тvr=пħ. Так как в задаче требуется определить величины, относящиеся к первой орбите, то главное квантовое число n=1 и указанное выше равенство примет вид

mvr=ħ. (1)

Для определения двух неизвестных величин r и v необходимо еще одно уравнение. В качестве второго уравнения воспользуемся уравнением движения электрона. Согласно теории Бора, электрон вращается вокруг ядра. При этом сила взаимодействия между электрическими зарядами ядра и электрона сообщает электрону центростремительное ускорение. На основании второго закона Нью­тона можем записать

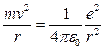
(е и m — заряд и масса электрона), или

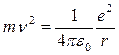(2)

Совместное решение равенств (1) и (2) относительно r дает

r = 4πε₀ ħ/(me²).

Подставив сюда значения ħ, е, т и произведя вычисления, най­дем боровский радиус:

r = а = 5,29∙10^{-11 м.}

Из равенства (1) получим выражение скорости электрона на первой орбите:

υ= ħ /(mr).

Произведя вычисления по этой формуле, найдем

υ = 2,18 Мм/с.

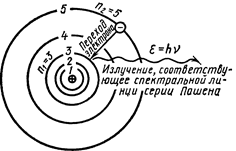
Пример 15. Определить энергию ε фотона, соответствующего вто­рой линии в первой инфракрасной серии (серии Пашена) атома водорода.

Решение. Энергия ε фотона, излучаемого атомом водорода при переходе электрона с одной орбиты на другую,

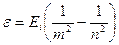
Рис.8

где E_i — энергия иониза­ции атома водорода; m=1,2,3,...—номер орбиты, на которую переходит электрон (рис. 8); n=m+1;

m+2;...— номер орбиты, с которой переходит электрон. Для серии Пашена m=3; для второй линии этой серии n= 3+2=5.

Подставив числовые значения, найдем энергию фотона:

ε = 0,97 эВ.

Пример 16. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля l для двух случаев: 1) U₁= = 51 кВ; 2) U₂= 510 кВ.

Решение. Длина волны де Бройля l частицы зависит от ее импульса р и определяется формулой

l = 2pħ/p (1)

Импульс частицы можно определить, если известна ее кинетичес­кая энергия Т. Связь импульса с кинетической энергией для не­релятивистского (когда T<<E₀) и для релятивистского (когда T » E₀) случаев соответственно выражается формулами:

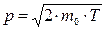; (2)

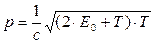(3)

Формула (1) с учетом соотношений (2) и (3) запишется соответ­ственно в нерелятивистском и релятивистском случаях:

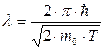; (4)

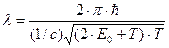(5)

Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U₁ = 51 В и U₂ = 510 кВ, с энергией покоя электрона и в зависимости от этого решим вопрос, которую из формул (4) и (5) следует применить для вычисления длины волны де Бройля.

Как известно, кинетическая энергия электрона, прошедшего ус­коряющую разность потенциалов U,

T = |e|U.

В первом случае T₁ = |e|(U₁ = 51 эВ = 0,51×10^-4 МэВ, что много меньше энергии покоя электрона E₀ = m₀c² = 0,51 МэВ. Следователь­но, можно применить формулу (4).

Для упрощения расчетов заметим, что T₁ = 10^-4 m⁰c². Подставив это выражение в формулу (4), перепишем ее в виде

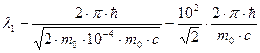
Учтя, что 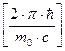есть комптоновская длина волны l_C, получим .

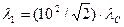Так как l_C = 2,43×10^{-12 м}, то

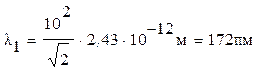
Во втором случае кинетическая энергия Т₂= ½е½ U₂ = 510 кэВ = 0,51 МэВ, т. е. равна энергии покоя электрона. Следовательно, необходимо применить релятивистскую формулу (5).

Учтя, что Т₂ =0,51 МэВ=mc², по формуле (5) найдем

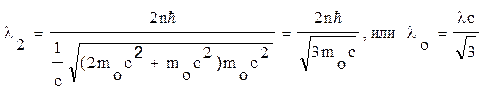
Подставив значение l_с в последнюю формулу и произведя вы­числения, получим

l₂=1,4 пм.

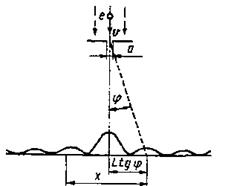
Пример 17. На узкую щель шириной а = 1 мкм направлен парал­лельный пучок электронов, имеющих скорость = 3,65 Мм/с. Учи­тывая волновые свойства электронов, определить расстояние х между двумя максимумами интенсивности первого порядка в дифракционной картине, полученной на экране, отстоящем на L = 10 см от щели.

Решение.Согласно гипотезе де Бройля, длина волны l, соответствующая частице массой т, движущейся со скоростью, выражается формулой

l = 2pħ/(mu). (1)

Дифракционный максимум при дифракции на одной щели наб­людается при условии

a sin j = (2k+1)(l/2), (2)

где k = 0, 1, 2, 3, . . .—порядко­вый номер максимумов; a — ши­рина щели.

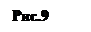Для максимумов первого порядка (k=1) угол j заведомо мал, по­этому sin j = j, и, следовательно, формула (2) примет вид

aj = ³/₂l, (3)

а искомая величина х, как следует из рис. 9,

x = 2L tg j = 2Lj, (4)

так как tg j = j.

Получим

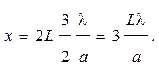
Подстановка в последнее равенство длины волны де Бройля по формуле (1) дает

.

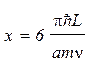После вычисления по формуле (5) получим

x = 6 · 10-41=60 мкм.