Динамика материальной точки и поступательного движения твердого тела
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
Кинематика поступательного движения материальной точки
Положение материальной точки в пространстве определяется с помощью радиус-вектора 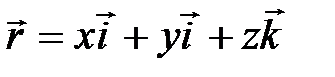 , где
, где 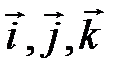 – единичные векторы – орты, направленные по осям прямоугольной системы координат,
– единичные векторы – орты, направленные по осям прямоугольной системы координат, 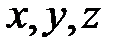 – координаты точки.
– координаты точки.
Кинематическое уравнение движения материальной точки: 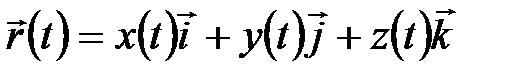 , где
, где 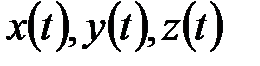 – функции, выражающие зависимость координат точки от времени.
– функции, выражающие зависимость координат точки от времени.
Средняя скорость:
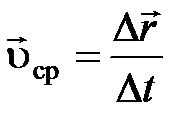 , где
, где 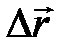 – вектор перемещения за время
– вектор перемещения за время 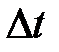 .
.
Средняя путевая скорость:
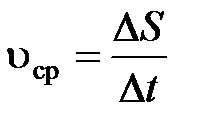 , где
, где 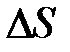 – путь, пройденный за время
– путь, пройденный за время 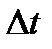 .
.
Мгновенная скорость:
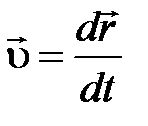 .
.
Среднее ускорение:
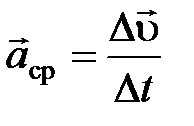 , где
, где 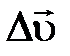 – приращение скорости за время
– приращение скорости за время 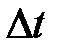 .
.
Мгновенное ускорение:
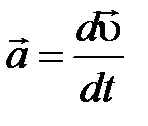 .
.
Полное ускорение при криволинейном движении:
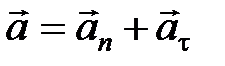 ,
, 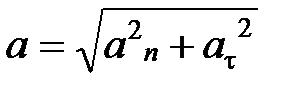 ,
,
где 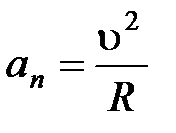 – нормальная составляющая ускорения,
– нормальная составляющая ускорения, 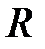 – радиус кривизны траектории:
– радиус кривизны траектории: 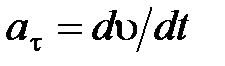 – тангенциальная составляющая ускорения.
– тангенциальная составляющая ускорения.
Длина пути, пройденного точкой за промежуток времени от 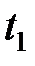 до
до 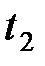 :
:
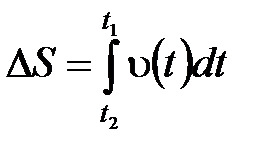 .
.
Координата материальной точки:
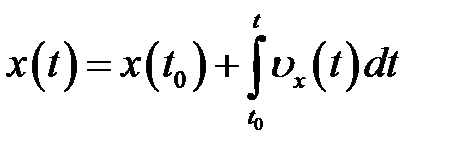 .
.
Кинематика вращательного движения материальной точки
Средняя угловая скорость: 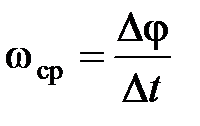 , где
, где 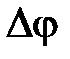 – угол поворота за время
– угол поворота за время 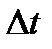 .
.
Мгновенная угловая скорость: 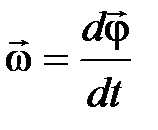 .
.
Линейная скорость 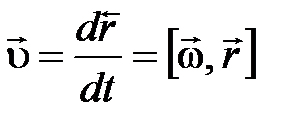 .
.
Среднее угловое ускорение 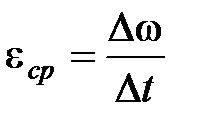 , где
, где 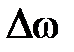 – приращение угловой скорости за время
– приращение угловой скорости за время 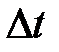 .
.
Мгновенное угловое ускорение 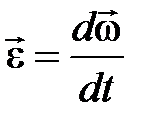 .
.
Тангенциальное ускорение 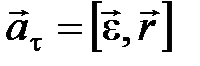 .
.
Нормальное ускорение 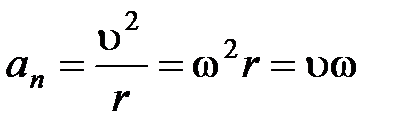 .
.
Угол поворота: 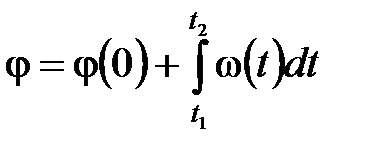 .
.
| Прямолинейное движение | Движение по окружности |
| Равномерное движение | |
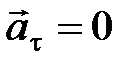 ; ; 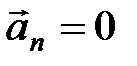 ; ; 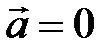 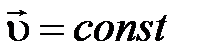 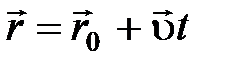 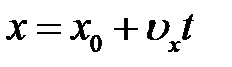 | 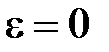 ; ; 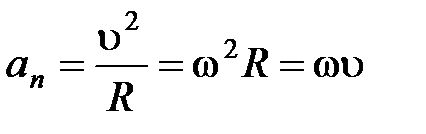 ; ; 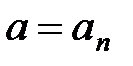 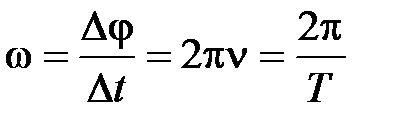 ; ; 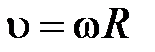 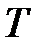 – период, – период, 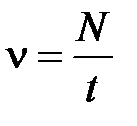 – частота вращения, N – число оборотов. – частота вращения, N – число оборотов. |
| Равнопеременное движение | |
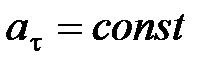 ; ; 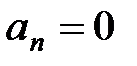 ; ;  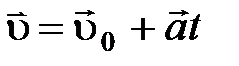 ; ; 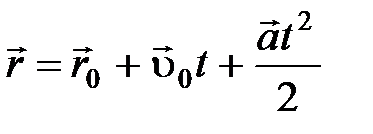 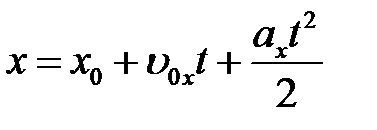 . . 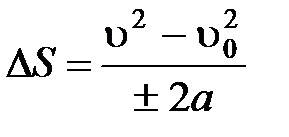 ; «+» – для равноускоренного движения; «-» – для равнозамедленного движения. ; «+» – для равноускоренного движения; «-» – для равнозамедленного движения. | 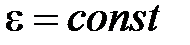 ; ; 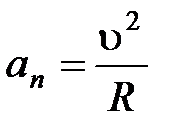 = = 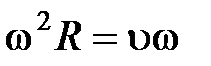 ; ; 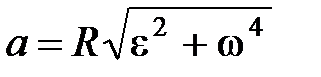 , , 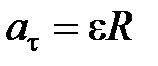  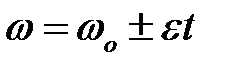 ; ; 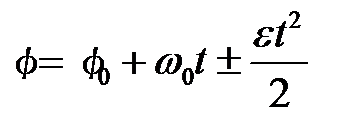 ; ; 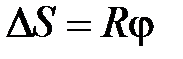 ; ; 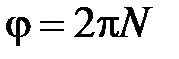 . «+» – для равноускоренного движения; «-» – для равнозамедленного движения. . «+» – для равноускоренного движения; «-» – для равнозамедленного движения. |
Относительность движения.
Сложение перемещений: 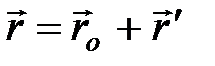 , где
, где 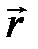 – перемещение точки относительно неподвижной системы отсчета;
– перемещение точки относительно неподвижной системы отсчета; 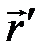 – перемещение точки относительно подвижной системы отсчета:
– перемещение точки относительно подвижной системы отсчета: 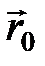 – перемещение подвижной системы отсчета относительно неподвижной.
– перемещение подвижной системы отсчета относительно неподвижной.
Закон сложения скоростей: 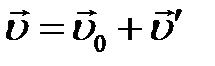 , где
, где 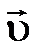 – скорость движения тела относительно неподвижной системы отсчета;
– скорость движения тела относительно неподвижной системы отсчета; 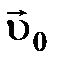 – скорость движения подвижной системы отсчета относительно неподвижной,
– скорость движения подвижной системы отсчета относительно неподвижной, 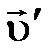 – скорость движения тела относительно подвижной системы отсчета.
– скорость движения тела относительно подвижной системы отсчета.
Динамика материальной точки и поступательного движения твердого тела
Импульс материальной точки 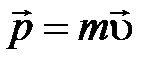 .
.
Импульс системы материальных точек 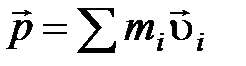 .
.
Второй закон Ньютона (основное уравнение динамики материальной точки): 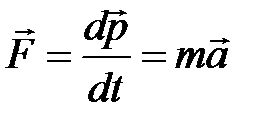 ,
,
где 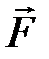 – равнодействующая всех сил, действующих на точку.
– равнодействующая всех сил, действующих на точку.
Изменение импульса материальной точки за промежуток времени от 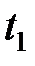 до
до 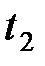 :
:
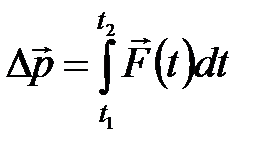 .
.
Радиус – вектор центра масс: 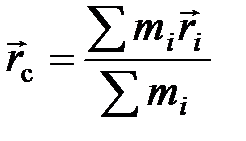 .
.
Закон сохранения импульса для замкнутой системы: 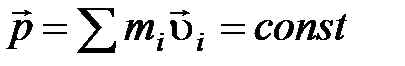 .
.
Взаимодействия в природе.
Сила гравитационного взаимодействия: 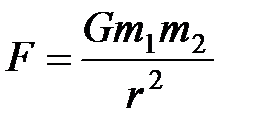 , где
, где 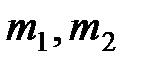 – массы взаимодействующих материальных точек, кг;
– массы взаимодействующих материальных точек, кг; 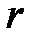 – расстояние между телами,м;
– расстояние между телами,м; 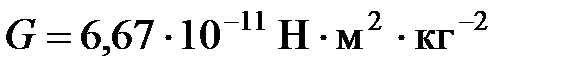 – гравитационная постоянная.
– гравитационная постоянная.
Сила тяжести 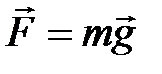 , где
, где 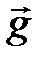 – ускорение свободного падения м/с2:
– ускорение свободного падения м/с2:
· ‑ на поверхности Земли: 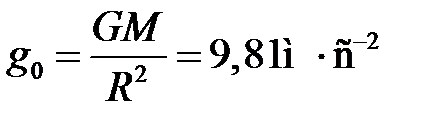 , где
, где 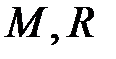 – масса и радиус Земли;
– масса и радиус Земли;
· ‑ на высоте 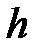 над поверхностью Земли:
над поверхностью Земли: 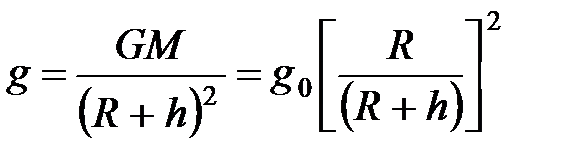 ;
;
· ‑ на глубине 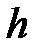 от поверхности Земли:
от поверхности Земли:
· 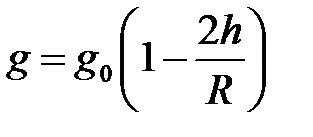 при h « R.
при h « R.
·
Первая космическая скорость вблизи поверхности Земли:
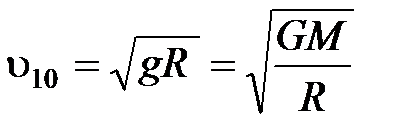 .
.
Первая космическая скорость на высоте h от поверхности Земли:
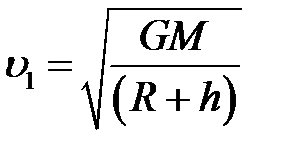 .
.
Вторая космическая скорость:
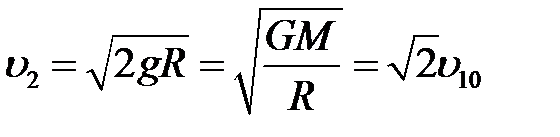 .
.
Закон Гука для продольного упругого растяжения (сжатия): 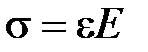 , где
, где 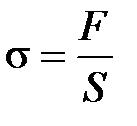 – нормальное напряжение, Па; F – сила упругости, Н;
– нормальное напряжение, Па; F – сила упругости, Н; 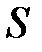 – площадь поперечного сечения образца, м2;
– площадь поперечного сечения образца, м2; 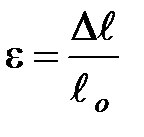 – относительное удлинение,
– относительное удлинение, 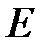 – модуль Юнга или модуль упругости, Па. Для упругой пружины закон Гука принято записывать в виде
– модуль Юнга или модуль упругости, Па. Для упругой пружины закон Гука принято записывать в виде 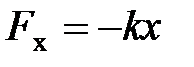 , где k – коэффициент жесткости, x – деформация.
, где k – коэффициент жесткости, x – деформация.
Сила трения скольжения: 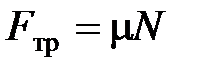 , где
, где 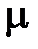 – коэффициент трения скольжения;
– коэффициент трения скольжения; 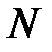 – сила реакции опоры.
– сила реакции опоры.
Механическая работа и мощность.
Элементарная работа:
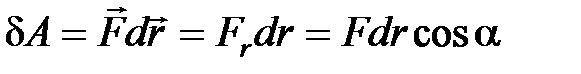 ,
,
где 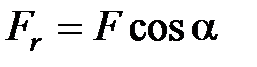 – проекция силы на направление перемещения
– проекция силы на направление перемещения 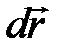 ;
; 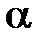 – угол между направлением силы и перемещения.
– угол между направлением силы и перемещения.
Работа, совершаемая переменной силой на пути:
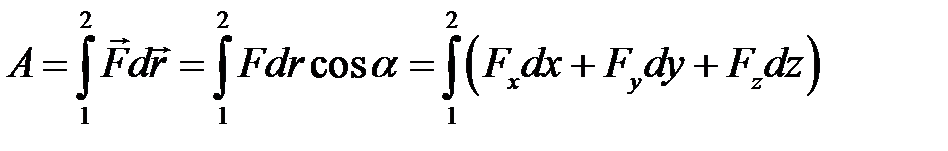 .
.
Работа силы тяжести вблизи поверхности Земли: 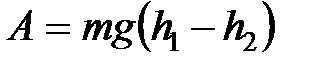 , где
, где 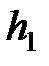 и
и 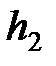 – начальная и конечная высота тела относительно начала отсчёта.
– начальная и конечная высота тела относительно начала отсчёта.
Работа силы упругости при деформации пружины: 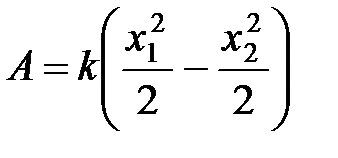 ,
,
где 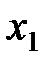 и
и 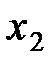 – начальная и конечная величина линейной деформации.
– начальная и конечная величина линейной деформации.
Работа силы трения: 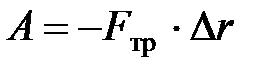 .
.
Средняя мощность за интервал времени Δt: 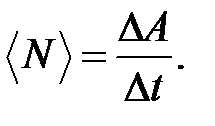
Мгновенная мощность: 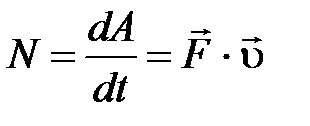 .
.
Коэффициент полезного действия:
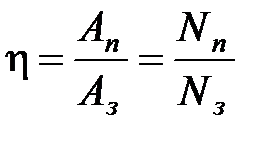 (%), где
(%), где 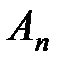 ,
, 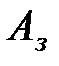 ,
, 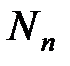 ,
, 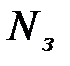 – соответственно полезные и затраченные работа и мощность.
– соответственно полезные и затраченные работа и мощность.
Кинетическая энергия материальной точки (или тела), движущейся поступательно:
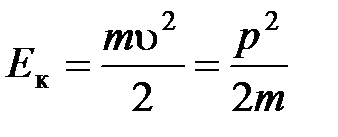 , где m – масса тела,
, где m – масса тела, 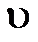 – его скорость, p – импульс.
– его скорость, p – импульс.
Потенциальная энергия тела и .консервативная сила, действующая на тело в данной точке:
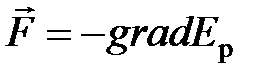 ;
; 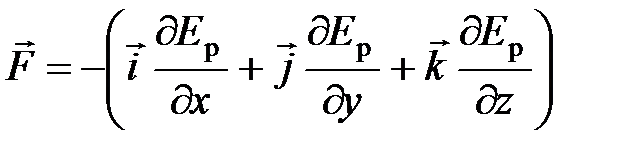 ,
,
где 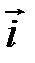 ,
,  ,
, 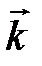 – единичные векторы координатных осей.
– единичные векторы координатных осей.
Потенциальная энергия:
· упруго деформированного тела: 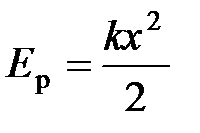 ;
; 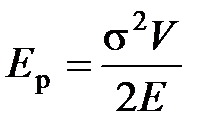 – потенциальная энергия упругого деформированного тела при растяжении – сжатии;
– потенциальная энергия упругого деформированного тела при растяжении – сжатии;  – напряжение,
– напряжение, 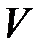 – объем тела,
– объем тела, 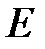 – модуль Юнга;
– модуль Юнга; 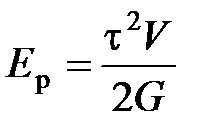 - потенциальная энергия упруго деформированного тела при деформации сдвига, где
- потенциальная энергия упруго деформированного тела при деформации сдвига, где 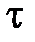 – касательное напряжение,
– касательное напряжение, 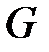 – модуль сдвига.
– модуль сдвига.
· гравитационного взаимодействия двух частиц: 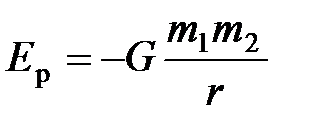 ;
;
· тела в однородном гравитационном поле: 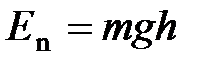 , где
, где 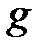 – напряжённость гравитационного поля (ускорение свободного падения);
– напряжённость гравитационного поля (ускорение свободного падения); 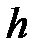 – расстояние от нулевого уровня потенциальной энергии.
– расстояние от нулевого уровня потенциальной энергии.
Динамика вращательного движения
Момент инерции материальной точки относительно оси вращения:
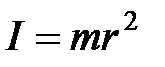 , где
, где 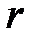 – расстояние до оси вращения.
– расстояние до оси вращения.
Момент инерции системы материальных точек (тела): 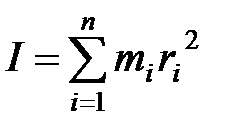 , где
, где 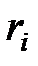 – расстояние
– расстояние 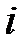 –ой материальной точки массой
–ой материальной точки массой 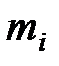 до оси вращения.
до оси вращения.
В случае непрерывного распределения масс 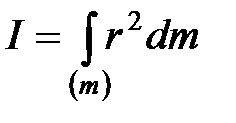 .
.
Теорема Штейнера: момент инерции тела массой m относительно неподвижной оси вращения, не проходящей через центр масс и параллельной оси вращения тела: 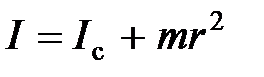 , где
, где 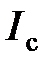 – момент инерции тела относительно оси, проходящей через центр масс,
– момент инерции тела относительно оси, проходящей через центр масс, 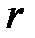 – расстояние между осями.
– расстояние между осями.
Момент инерции тел правильной геометрической формы относительно неподвижной оси вращения.
| Форма тела | Ось вращения | Момент инерции |
1.Однородный шар радиусом 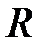 и массой и массой 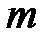 | проходит через центр масс | 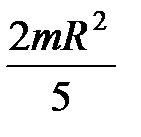 |
2.Круглый однородный цилиндр или диск радиусом 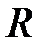 и массой и массой 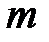 | проходит через центр масс перпендикулярно плоскости основания | 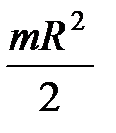 |
3.Тонкий обруч или кольцо радиусом 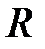 и массой и массой 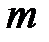 | проходит через центр масс перпендикулярно плоскости обруча | 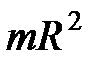 |
4.Однородный тонкий стержень длиной 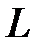 и массой и массой 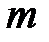 | проходит через центр масс стержня перпендикулярно стержню | 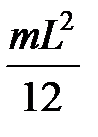 |
| проходит через конец стержня перпендикулярно стержню | 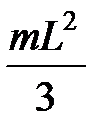 |
Момент силы относительно произвольной точки:
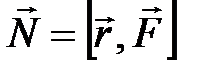 , где
, где 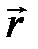 – радиус-вектор, проведенный из этой точки в точку приложения силы
– радиус-вектор, проведенный из этой точки в точку приложения силы 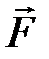 .
.
Модуль момента силы относительно оси: 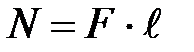 , где
, где 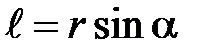 – плечо силы (кратчайшее расстояние между линией действия силы и осью вращения).
– плечо силы (кратчайшее расстояние между линией действия силы и осью вращения).
Момент импульса твердого тела относительно оси вращения.
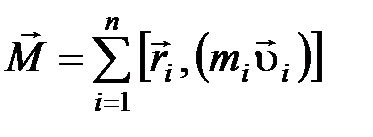 ;
; 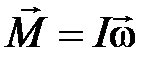 ,
,
где 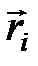 – радиус–вектор отдельной
– радиус–вектор отдельной 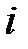 -ой частицы;
-ой частицы; 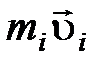 – импульс этой частицы;
– импульс этой частицы; 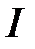 – момент инерции тела относительно оси;
– момент инерции тела относительно оси; 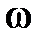 – угловая скорость.
– угловая скорость.
Основное уравнение (закон) динамики вращательного движения
· относительно неподвижной точки: 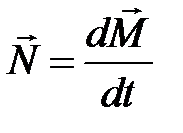 , где
, где 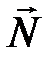 - главный (результирующий) момент всех внешних сил, действующих на систему относительно неподвижной точки О;
- главный (результирующий) момент всех внешних сил, действующих на систему относительно неподвижной точки О; 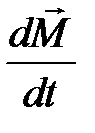 - скорость изменения момента импульса системы относительно той же точки;
- скорость изменения момента импульса системы относительно той же точки;
· относительно неподвижной оси z:, 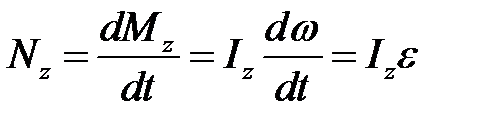 , где
, где 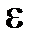 – угловое ускорение,
– угловое ускорение, 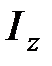 – момент инерции тела относительно оси.
– момент инерции тела относительно оси.
Закон сохранения момента импульса для замкнутой системы:
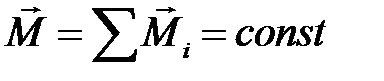 или
или 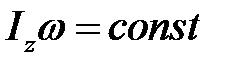 .
.
Элементарная работа при вращении тела: 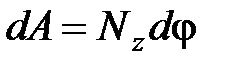 , где
, где 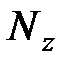 – момент силы относительно оси;
– момент силы относительно оси; 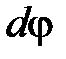 – элементарный угол поворота тела.
– элементарный угол поворота тела.
Кинетическая энергия тела, вращающегося вокруг неподвижной оси:
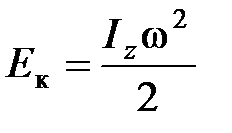 .
.
Кинетическая энергия тела, катящегося по плоскости без скольжения:
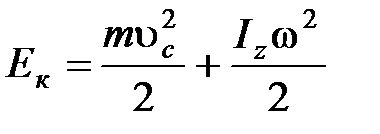 , где
, где 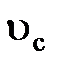 – скорость центра масс тела,
– скорость центра масс тела, 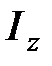 – момент инерции тела относительно оси, проходящей через центр масс.
– момент инерции тела относительно оси, проходящей через центр масс.
Условия равновесия тела.
Векторная сумма всех сил, действующих на тело, равна нулю: 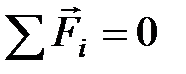 .
.
Векторная сумма моментов всех сил, действующих на тело, равна нулю: 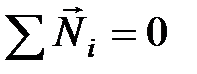 .
.
Элементы механики жидкостей
Гидростатическое давление столба жидкости высотой 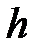 :
: 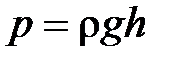 , где
, где 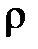 – плотность жидкости, кг/м3.
– плотность жидкости, кг/м3.
Закон Архимеда: 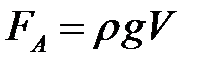 , где
, где 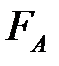 – выталкивающая сила:
– выталкивающая сила: 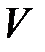 – объем погружённой части тела.
– объем погружённой части тела.
Уравнение неразрывности струи: 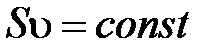 ,где
,где 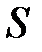 – площадь поперечного сечения трубки тока;
– площадь поперечного сечения трубки тока; 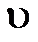 – скорость движения жидкости в этом сечении.
– скорость движения жидкости в этом сечении.
Уравнение Бернулли для стационарного течения идеальной жидкости:
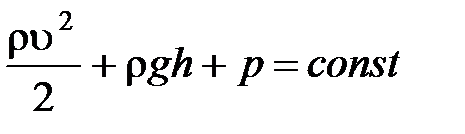 ,
,
где 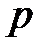 – статическое давление жидкости для определенного сечения трубки тока;
– статическое давление жидкости для определенного сечения трубки тока; 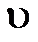 – скорость жидкости для этого сечения;
– скорость жидкости для этого сечения; 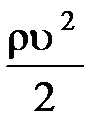 – динамическое давление жидкости для этого сечения;
– динамическое давление жидкости для этого сечения; 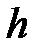 – высота, на которой располагается сечение;
– высота, на которой располагается сечение; 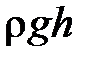 – гидростатическое давление.
– гидростатическое давление.
Скорость истечения жидкости из малого отверстия в открытом сосуде
(формула Торичелли): 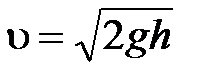 , где
, где 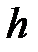 – глубина, на которой находится отверстие относительно уровня жидкости в сосуде.
– глубина, на которой находится отверстие относительно уровня жидкости в сосуде.
Формула Стокса, определяющая силу сопротивления F, действующую со стороны потока жидкости на медленно движущийся в ней шарик:
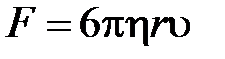 , где r – радиус шарика, u – его скорость.
, где r – радиус шарика, u – его скорость.
