Проходження мікрочастинки через
Потенціальний бар’єр
17.1 Мета роботи
Дослідити явище проходження мікрочастинки через потенціальний бар’єр та отримати залежність ймовірності проходження мікрочастинки через такий бар’єр від його висоти, ширини і форми.
17.2 Вказівки з організації самостійної роботи
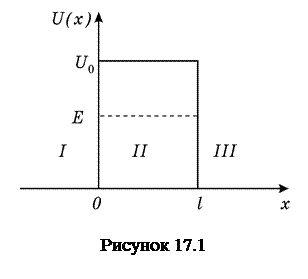 Нехай частинка, що рухається зі сторони від'ємних значень х, зустрічає бар'єр висотою
Нехай частинка, що рухається зі сторони від'ємних значень х, зустрічає бар'єр висотою 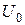 і шириною l (рис.17.1). Згідно з квантовою механікою, існує ймовірність того, що частинка відіб'ється від бар'єра при
і шириною l (рис.17.1). Згідно з квантовою механікою, існує ймовірність того, що частинка відіб'ється від бар'єра при 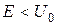 . Існує також певна ймовірність того, що частинка проникне через бар'єр, навіть якщо її енергія
. Існує також певна ймовірність того, що частинка проникне через бар'єр, навіть якщо її енергія 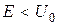 (тунельний ефект). Розглянемо цей випадок. Рівняння Шредінгера для областей І і ІІІ має такий вигляд [3, 6]:
(тунельний ефект). Розглянемо цей випадок. Рівняння Шредінгера для областей І і ІІІ має такий вигляд [3, 6]:
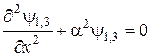 , (17.1)
, (17.1)
а для області ІІ, причому 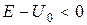 :
:
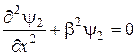 , (17.2)
, (17.2)
де 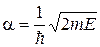 ,
, 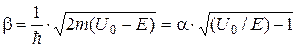 . (17.3)
. (17.3)
Загальний розв’язок рівняння (17.1) має такий вигляд:
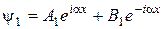 для області І, (17.4)
для області І, (17.4)
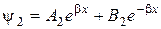 для області ІІ, (17.5)
для області ІІ, (17.5)
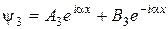 для області ІІІ. (17.6)
для області ІІІ. (17.6)
Слід відзначити, що вираз вигляду 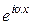 відповідає хвилі, яка розповсюд-
відповідає хвилі, яка розповсюд-
жується в додатному напрямку осі х, а вигляду 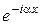 – хвилі, що розповсюд-
– хвилі, що розповсюд-
жується в протилежному напрямку.
В області ІІІ є лише хвиля, що пройшла через бар’єр і розповсюджується зліва направо (рис.17.1). Тому коефіцієнт 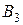 у виразі (17.5) для
у виразі (17.5) для 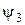 слід брати рівним нулю.
слід брати рівним нулю.
Задовольняючи граничним умовам безперервності 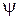 -функції, а також безперервності її похідної
-функції, а також безперервності її похідної
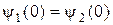 ,
, 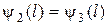 , (17.7)
, (17.7)
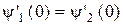 ,
, 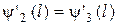
отримуємо таку систему рівнянь для визначення невідомих коефіцієнтів 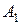 ,
, 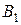 ,
, 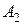 ,
, 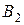 ,
, 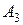 :
:
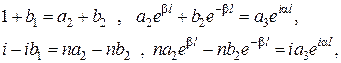 (17.8)
(17.8)
де 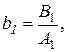
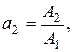
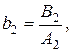
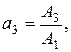
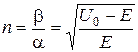 .
.
Відношення квадратів модулів амплітуд відбитої і падаючої хвиль
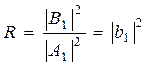 (17.9)
(17.9)
визначає ймовірність відбиття частинки від бар'єра і називається коефіцієнтом відбиття.
Відношення квадратів модулів амплітуд пройденої і падаючої хвиль:
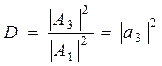 (17.10)
(17.10)
визначає ймовірність проходження частинки через бар'єр і називається коефіцієнтом проходження. Коефіцієнти R і D пов'язані співвідношенням
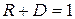 . (17.11)
. (17.11)
Розв’язуючи систему (17.8), отримуємо вирази для коефіцієнтів 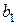 ,
, 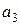
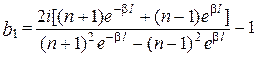 , (17.12)
, (17.12)
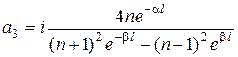 .
.
через які визначаються коефіцієнти проходження та відбивання (17.9), (17.10) (для спрощення обчислень вибираємо коефіцієнт 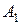 =1 ).
=1 ).
Величина 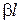 , як правило, буває набагато більше одиниці. Якщо в формулах (17.12) покласти
, як правило, буває набагато більше одиниці. Якщо в формулах (17.12) покласти 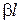 >>1, то для коефіцієнта проходження можна отримати наближений вираз
>>1, то для коефіцієнта проходження можна отримати наближений вираз
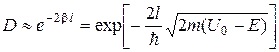 . (17.13)
. (17.13)
Із отриманого виразу (17.13) випливає, що ймовірність проходження залежить від ширини бар'єра l, співвідношення між енергією частинки Е і висотою потенціального бар'єра та від маси частинки m.
Для точних виразів коефіцієнтів відбивання R та проходження D складена програма обчислень, яка дозволяє вивчити їх залежність від параметрів l, E, 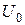 та m.
та m.
17.3 Опис комп’ютерної програми
Інтерфейс програми зображено на рис. 17.2 і 17.3. В режимі “Прямокутний бар’єр” програма обчислює точні вирази коефіцієнтів y-функцій (17.9)...(17.12) в трьох областях, на які поділяє простір прямокутний бар’єр (рис.17.1), коефіцієнти прозорості D та відбивання R мікрочастинки, вирисовують графік модуля y-функції, та її реальну частину. Програма рисує графіки залежності коефіцієнта відбивання та прозорості від відношення енергії частинки до висоти бар’єра 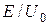 при сталих значеннях ширини бар’єра та маси частинки. Програма також дає можливість провести обчислення коефіцієнта D за наближеною формулою (17.13) та встановити її область застосування.
при сталих значеннях ширини бар’єра та маси частинки. Програма також дає можливість провести обчислення коефіцієнта D за наближеною формулою (17.13) та встановити її область застосування.
17.4 Інструкція користувачу
1. Ознайомитись із змістом “Help” (клавіша F1).
2. Для значення маси 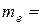 9,11∙10-31 кг, ширини бар’єра
9,11∙10-31 кг, ширини бар’єра 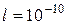 м, та
м, та 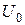 , взятого з табл. 17.1, отримати на екрані графіки
, взятого з табл. 17.1, отримати на екрані графіки 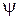 та
та 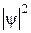 , зарисувати. Для порівняння зробити те саме для m,
, зарисувати. Для порівняння зробити те саме для m, 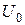 та l, взятих з таблиці варіантів (графіки не зарисовувати).
та l, взятих з таблиці варіантів (графіки не зарисовувати).

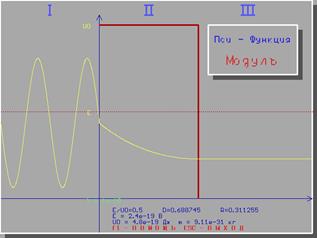
Рисунок 17.2 Рисунок 17.3
3. Для величин m, 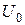 , l, взятих з таблиці, отримати на екрані графіки коефіцієнтів D і R в залежності від відношення
, l, взятих з таблиці, отримати на екрані графіки коефіцієнтів D і R в залежності від відношення 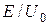 . Повторити розрахунки для шести значень l, змінюючи l кожного разу на Dl=0,2·10-12 м. Зарисувати всі сім графіків
. Повторити розрахунки для шести значень l, змінюючи l кожного разу на Dl=0,2·10-12 м. Зарисувати всі сім графіків 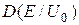 на одному рисунку.
на одному рисунку.
4. Для двох значень відношення 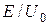 =0,5; 0,8 побудувати графіки залежності D від ширини бар’єра l , користуючись результатами пункту 3.
=0,5; 0,8 побудувати графіки залежності D від ширини бар’єра l , користуючись результатами пункту 3.
5. Отримати на екрані графіки коефіцієнтів D і R в залежності від 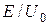 для семи значень маси (значення маси для всіх варіантів однакові: від 1,9 до 30·10-28 кг, які наведені в таблиці). Зарисувати графіки для коефіцієнта D на одному рисунку.
для семи значень маси (значення маси для всіх варіантів однакові: від 1,9 до 30·10-28 кг, які наведені в таблиці). Зарисувати графіки для коефіцієнта D на одному рисунку.
6. Користуючись результатами пункту 5 побудувати для двох значень відношення 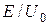 =0,5; 0,8 графіки залежності коефіцієнта прозорості від маси.
=0,5; 0,8 графіки залежності коефіцієнта прозорості від маси.
7. Побудувати графік 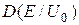 за наближеною формулою (17.13) та порівняти його з результатами точного розрахунку . Дані взяти з табл. 17.1.
за наближеною формулою (17.13) та порівняти його з результатами точного розрахунку . Дані взяти з табл. 17.1.
8. Встановити (змінюючи l ) , при якому значенні
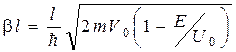
похибка під час обчислення D за формулою (17.13) не перевищує 10%, 3%.
17.5 Зміст звіту
Звіт має містити: мету роботи; рисунок бар’єра; всі графічні залежності, отримані за пунктами 2...7; висновки, які виходять із графіків щодо залежності коефіцієнта прозорості D від відносної висоти бар’єра 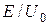 , ширини бар’єра та маси частинки ; висновки щодо застосування наближеної формули (17.13).
, ширини бар’єра та маси частинки ; висновки щодо застосування наближеної формули (17.13).
Таблиця 17.1 – Вихідні дані
| Номер вар. | Позначення частинки | m·10-28, кг | 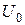 , еВ , еВ | l·10-12, м |
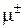 (мезон) (мезон) | 1,9 | |||
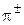 (мезон) (мезон) | 2,5 | 3,5 | ||
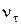 (лептон) (лептон) | 4,5 | |||
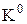 (мезон) (мезон) | 8,9 | 2,5 | ||
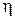 (мезон) (мезон) | 9,8 | |||
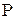 (протон) (протон) | 1,5 | |||
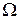 (гіперон) (гіперон) | ||||
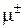 (мезон) (мезон) | 1,9 | |||
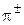 (мезон) (мезон) | 2,5 | |||
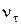 (лептон) (лептон) | 4,5 | 3,5 | ||
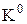 (мезон) (мезон) | 8,9 | |||
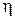 (мезон) (мезон) | 9,8 | 2,5 | ||
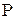 (протон) (протон) | ||||
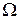 (гіперон) (гіперон) | 1,5 |
17.6 Контрольні запитання і завдання
1. Що таке “потенціальний бар’єр” та “висота потенціального бар’єра?
2. Чи може відбиватись частинка від бар’єра у випадку коли її енергія 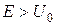 ; проходити крізь бар’єр, коли
; проходити крізь бар’єр, коли 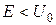 ?
?
3. Запишіть рівняння Шредінгера всередині бар’єра та за його межами.
4. Який вигляд має 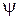 -функція в трьох різних областях, на які поділяє простір бар’єр?
-функція в трьох різних областях, на які поділяє простір бар’єр?
5. Який експоненціальний множник із множників 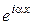 ,
, 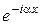 відповідає хвилі, що розповсюджується в напрямку позитивних значень х, негативних значень х?
відповідає хвилі, що розповсюджується в напрямку позитивних значень х, негативних значень х?
6. Яким граничним умовам має задовольняти 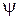 -функція та її похідна на межах бар’єра?
-функція та її похідна на межах бар’єра?
7. Як визначається коефіцієнт проходження (прозорості) D, коефіцієнт відбивання R частинки?
8. Яке співвідношення пов’язує R і D?
9. Що визначають коефіцієнти R і D в квантовій механіці?
