Эти результаты также занесите в таблицу
8. Вычислите относительную погрешность измерения
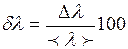 (%)
(%)
и запишите окончательный результат работы в виде:
λ = < λ > ± Δλ (нм) с δλ = … (%).
Контрольные вопросы
1. Сформулируйте принцип Гюйгенса – Френеля.
2. Какие источники световых волн называются когерентными?
3. В чём заключается явление дифракции?
4. Опишите устройство дифракционной решётки.
5. Почему дифракционная решетка разлагает белый свет в спектр?
Контрольная работа № 3
Вариант 0.
Задача № 1 (310). Расстояние d между двумя точечными зарядами Q1 = 2 нКл и Q2 = 4нКл равно 60 см. Определить точку, в которую нужно поместить третий заряд Q3 так, чтобы система зарядов находилась в равновесии. Определить заряд Q3 и его знак. Устойчивое или неустойчивое будет равновесие?
Задача № 2 (340).Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда τ = 200 пКл/м. Определить потенциал φ поля в точке пересечения диагоналей.
Задача № 3 (350). Электрон движется вдоль силовой линии однородного электрического поля. В некоторой точке поля с потенциалом φ1 =100 В электрон имел скорость v1 = 6 Мм/с. Определить потенциал φ2 точки поля, дойдя до которой электрон потеряет половину своей скорости.
Задача № 4 (360). Плоский конденсатор с площадью пластин S = 200 см2 каждая заряжен до разности потенциалов U = 2 кВ. Расстояние между пластинами d = 2 см. Диэлектрик – стекло. Определить энергию W поля конденсатора и плотность энергии w поля.
Задача № 5 (370). ЭДС батареи 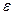 = 12 В. При силе тока I = 4 А. КПД батареи η = 0.6. Определить внутреннее сопротивление Ri батареи.
= 12 В. При силе тока I = 4 А. КПД батареи η = 0.6. Определить внутреннее сопротивление Ri батареи.
| Задача № 6 (410). Бесконечно длинный провод с током I = 50 А изогнут так, как это показано на рисунке. Определить магнитную индукцию В в точке А, лежащей на биссектрисе прямого угла на расстоянии d = 10 см от его вершины. | 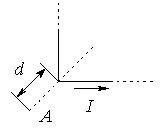 |
Задача № 7 (470). Кольцо из медного провода массой m = 10 г помещено в однородное магнитное поле (В = 0.5 Тл) так, что плоскость кольца составляет угол β = 60˚ с линиями магнитной индукции. Определить заряд Q, который пройдет по кольцу, если снять магнитное поле.
Задача № 8 (520). Расстояние между штрихами дифракционной решетки d = 4мкм. На решетку падает нормально свет с длиной волны 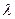 = 0.58 мкм. Максимум какого наибольшего порядка дает эта решетка?
= 0.58 мкм. Максимум какого наибольшего порядка дает эта решетка?
Задача № 9 (550). Средняя энергетическая светимость R поверхности Земли равна 0,54 Дж/(см2·мин). Какова должна быть температура Т поверхности Земли, если условно считать, что она излучает как серое тело с коэффициентом черноты аr = 0.25 ?
Вариант 1. (Контрольная работа № 3).
Задача № 1 (301). Точечные заряды Q1 = 20 мкКл, Q2 = -10 мкКл находятся на расстоянии d = 5 см друг от друга. Определить напряженность поля в точке, удаленной на r1 = 3 см от первого и на r2 = 4 см от второго заряда. Определить также силу F, действующую в этой точке на точечный заряд Q = 1 мкКл.
Задача № 2 (331). Два точечных заряда Q1 = 6 нКл и Q2 = 3 нКл находятся на расстоянии d = 60 см друг от друга. Какую работу необходимо совершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?
Задача № 3 (341). Пылинка массой m = 200 мкг, несущая на себе заряд Q = 40нКл, влетела в электрическое поле в направление силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость υ = 10м/с. Определить скорость υ0 пылинки до того, как она влетела в поле.
Задача № 4 (351). Конденсаторы емкостью С1 = 5 мкФ и С2 = 10 мкФ заряжены до напряжений U1 = 60 В и U2 = 100 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими одноименные заряды.
Задача № 5 (361). Катушка и амперметр соединены последовательно и подключены к источнику тока. К клеммам катушки присоединен вольтметр с сопротивлением r = 4 кОм. Амперметр показывает силу тока I = 0.3 А, вольтметр – напряжение U = 120 В. Определить сопротивление R катушки. Определить относительную погрешность ξ, которая будет допущена при измерении сопротивления, если пренебречь силой тока, текущего через вольтметр.
| Задача № 6 (401). Бесконечно длинный провод с током I = 100 А изогнут так, как это показано на рисунке. Определить магнитную индукцию В в точке О. Радиус дуги R = 10 см. | 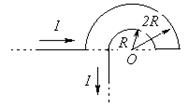 |
Задача № 7 (461). В однородном магнитном поле (В = 0.1 Тл) равномерно с частотой n = 5 с-1 вращается стержень длиной l = 50 см так, что плоскость его вращения перпендикулярна линиям напряженности, а ось вращения проходит через один из его концов. Определить индуцируемую на концах стержня разность потенциалов U.
Задача № 8 (511). Какое наименьшее число N min штрихов должна содержать дифракционная решетка, чтобы в спектре второго порядка можно было видеть раздельно две желтые линии натрия с длинами волн λ1 = 589.0 нм и λ2 = 589.6нм? Какова длина l такой решетки, если постоянная решетки d = 5 мкм?
Задача № 9 (541). Абсолютно черное тело имеет температуру Т1 = 500 К. Какова будет температура Т2 тела, если в результате нагревания поток излучения увеличится в n = 5 раз?
Вариант 2. (Контрольная работа № 3).
Задача № 1 (302). Три одинаковых точечных заряда Q1 = Q2 = Q3 = 2 нКл находятся в вершинах равностороннего треугольника со сторонами а = 10 см. Определить модуль и направление силы F, действующей на один из зарядов со стороны двух других.
| Задача № 2 (332). Электрическое поле создано заряженным проводящим шаром, потенциал φ которого 300 В. Определить работу сил поля по перемещению заряда Q = 0.2 мкКл из точки 1 в точку 2 (рисунок). | 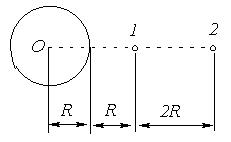 |
Задача № 3 (342). Электрон, обладавший кинетической энергией Т = 10 эВ, влетел в однородное электрическое поле в направление силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов U = 8 В?
Задача № 4 (352). Конденсатор емкостью С1 = 10 мкФ заряжен до напряжения U = 10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был подключен другой, незаряженный, конденсатор емкостью С2 = 20 мкФ.
Задача № 5 (362). ЭДС батареи 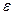 = 80 В, внутреннее сопротивление Ri = 5 Ом. Внешняя цепь потребляет мощность Р = 100 кВт. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, и ее сопротивление R.
= 80 В, внутреннее сопротивление Ri = 5 Ом. Внешняя цепь потребляет мощность Р = 100 кВт. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, и ее сопротивление R.
| Задача № 6 (402). Магнитный момент pm тонкого проводящего кольца pm = 5 А×м2. Определить магнитную индукцию В в точке А, находящейся на оси кольца и удаленной от точек кольца на расстояние r = 20 см (рисунок). | 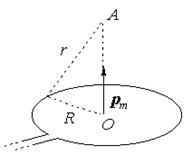 |
Задача № 7 (462). В однородном магнитном поле с индукцией В = 0.5 Тл вращается с частотой n = 10 с-1 стержень длиной l = 20 см. Ось вращения параллельна линиям индукции и проходит через один из концов стержня перпендикулярно его оси. Определить разность потенциалов U на концах стержня.
Задача № 8 (512). На поверхность дифракционной решетки нормально к ее поверхности падает монохроматический свет. Постоянная дифракционной решетки в n = 4.6 раза больше длины световой волны. Найти общее число М дифракционных максимумов, которые теоретически можно наблюдать в данном случае.
Задача № 9 (542). Черное тело имеет температуру Т1 = 500К. Какова будет температура Т2 тела, если в результате нагревания поток излучения увеличится в n = 5 раз?
Вариант 3. (Контрольная работа № 3).
Задача № 1 (303). Два положительных точечных заряда Q и 9Q закреплены на расстоянии d = 100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии.
| Задача № 2 (333). Электрическое поле создано зарядами Q1 = 2 мкКл и Q2 = -2 мкКл, находящимися на расстоянии а = 10 см друг от друга. Определить работу сил поля, совершаемую при перемещении заряда Q = 0.5 мкКл из точки l в точку 2 (рисунок). | 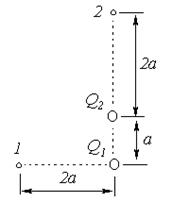 |
Задача № 3 (343). Найти отношение скоростей ионов Cu++ и К-, прошедших одинаковую разность потенциалов.
Задача № 4 (353). Конденсаторы емкостями С1 = 2 мкФ, С2 = 5 мкФ и С3 = 10мкФ соединены последовательно и находятся под напряжением U = 850 В. Определить напряжение и заряд на каждом из конденсаторов.
Задача № 5 (363). От батареи, ЭДС которой 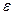 = 600 В, требуется передать энергию на расстояние l = 1 км. Потребляемая мощность Р = 5 кВт. Найти минимальные потери мощности в сети, если диаметр медных подводящих проводов d = 0.5 см.
= 600 В, требуется передать энергию на расстояние l = 1 км. Потребляемая мощность Р = 5 кВт. Найти минимальные потери мощности в сети, если диаметр медных подводящих проводов d = 0.5 см.
| Задача № 6 (403). По двум скрещенным под прямым углом бесконечно длинным проводам текут токи I и 2I (I = 100 А). Определить магнитную индукцию В в точке А (рисунок). Расстояние d = 10 см. | 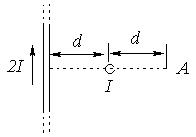 |
Задача № 7 (463). В проволочное кольцо, присоединенное к баллистическому гальванометру, вставили прямой магнит. При этом по цепи прошел заряд Q = 50 мкКл. Определить изменение магнитного потока DF через кольцо, если сопротивление цепи гальванометра R = 10 Ом.
Задача № 8 (513). На дифракционную решетку падает нормально параллельный пучок белого света. Спектры третьего и четвертого порядка частично накладываются друг на друга. На какую длину волны в спектре четвертого порядка накладывается граница ( 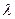 = 780 нм) спектра третьего порядка?
= 780 нм) спектра третьего порядка?
Задача № 9 (543). Температура абсолютно черного тела Т = 2 кК. Определить длину волны λm , на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости (излучательности) (rλ,T)max для этой длины волны.
Вариант 4. (Контрольная работа № 3).
Задача № 1 (304). Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол 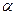 . Шарики погружают в масло. Какова плотность
. Шарики погружают в масло. Какова плотность 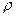 масла, если угол расхождения нитей при погружении в масло остается неизменным? Плотность материала шарика
масла, если угол расхождения нитей при погружении в масло остается неизменным? Плотность материала шарика 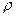 о = 1.5•103 кг/м3, диэлектрическая проницаемость масла
о = 1.5•103 кг/м3, диэлектрическая проницаемость масла 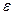 = 2.2.
= 2.2.
Задача № 2 (334). Две параллельные заряженные плоскости, поверхностные плотности заряда которых 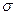 1 = 2 мкКл/м2 и
1 = 2 мкКл/м2 и 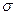 2 = -0,8 мкКл/м2 , находятся на расстоянии d = 0.6 см друг от друга. Определить разность потенциалов U между плоскостями.
2 = -0,8 мкКл/м2 , находятся на расстоянии d = 0.6 см друг от друга. Определить разность потенциалов U между плоскостями.
Задача № 3 (344). Электрон с энергией Т = 400 эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической запряженной сферы радиусом R = 10 см. Определить минимальное расстояние а, на которое приблизится электрон к поверхности сферы, если заряд ее Q = -10нКл.
Задача № 4 (354). Два конденсатора емкостями С1 = 2 мкФ и С2 = 5 мкФ заряжены до напряжений U1 =100 В и U2 =150 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.
Задача № 5 (364). При внешнем сопротивлении R1 = 8 Ом сила тока в цепи I1 = 0.8 А, при сопротивлении R2 = 15 Ом сила тока I2 = 0.5 А. Определить силу тока Iкз короткого замыкания источника ЭДС.
Задача № 6 (404). По бесконечно длинному проводу, изогнутому так, как это показано на рисунке, течет ток I = 200 А. Определить магнитную индукцию В в точке О. Радиус дуги R = 10 см. Угол 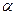 равен 2 равен 2 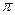 /3. /3. | 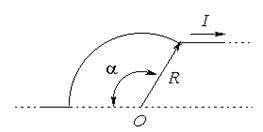 |
Задача № 7 (464). Тонкий медный провод массой m = 5 г согнут в виде квадрата, и концы его замкнуты. Квадрат помещен в однородное магнитное поле (В = 0.2 Тл) так, что его плоскость перпендикулярна линиям поля. Определить заряд Q, который потечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.
Задача № 8 (514). На дифракционную решетку, содержащую n = 600 штрихов на миллиметр, падает нормально белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить длину l спектра первого порядка на экране, если расстояние от линзы до экрана L = 1.2 м. Границы видимого спектра: 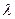 кр. = 780 нм,
кр. = 780 нм, 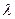 ф. = 400 нм.
ф. = 400 нм.
Задача № 9 (544). Определить температуру Т и энергетическую светимость (излучательность) Rе абсолютно черного тела, если максимум энергии излучения приходится на длину волны λm = 600 нм.
Вариант 5. (Контрольная работа № 3).
Задача № 1 (305). Четыре одинаковых заряда Q1 = Q2 = Q3 = Q4 = 2 нКл закреплены в вершинах квадрата со стороной а = 10 см. Найти силу F, действующую на один из этих зарядов со стороны трех остальных.
Задача № 2 (335). Диполь с электрическим моментом р = 100 пКл·м свободно установился в свободном электрическом поле напряженностью Е = 200 кВ/м. Определить работу внешних сил, которую необходимо совершить для поворота диполя на угол 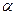 = 180º.
= 180º.
Задача № 3 (345). Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобрел скорость v = 103 м/с. Расстояние между пластинами d = 8 мм. Найти: 1) разность потенциалов U между пластинами; 2) поверхностную плотность заряда σ на пластинах.
Задача № 4 (355). Два одинаковых плоских воздушных конденсатора емкостью С = 100 пФ каждый соединены в батарею последовательно. Определить, на сколько изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.
Задача № 5 (365). ЭДС батареи 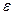 = 24 В. Наибольшая сила тока, которую может дать батарея, Imax = 10 А. Определить максимальную мощность Рmах, которая может выделяться во внешней цепи.
= 24 В. Наибольшая сила тока, которую может дать батарея, Imax = 10 А. Определить максимальную мощность Рmах, которая может выделяться во внешней цепи.
| Задача № 6 (405). По тонкому кольцу радиусом R = 20 см течет ток I = 100 А. Определить магнитную индукцию В на оси кольца в точке А (рисунок). Угол β = π/3. | 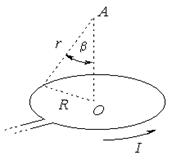 |
Задача № 7 (465). Рамка из провода сопротивлением R = 0.04 Ом равномерно вращается в однородном магнитном поле (В = 0.6 Тл). Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Площадь рамки S = 200см2.Определить заряд Q, который потечет по рамке при изменении угла между нормалью к рамке и линиями индукции: 1) от 0 до 45˚; 2) от 45 до 90˚.
Задача № 8 (515). На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения. Расстояние d между атомными плоскостями равно 280 пм. Под углом 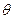 = 65о к атомной плоскости наблюдается дифракционный максимум первого порядка. Определить длину волны
= 65о к атомной плоскости наблюдается дифракционный максимум первого порядка. Определить длину волны 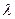 рентгеновского излучения.
рентгеновского излучения.
Задача № 9 (545). Из смотрового окошечка печи излучается поток Фе = 4кДж/мин. Определить температуру Т печи, если площадь окошечка S = 8 см2.
Вариант 6. (Контрольная работа № 3).
Задача № 1 (306). Точечные заряды Q1 = 30 мкКл и Q2 = -20 мкКл находятся на расстоянии d = 20 см друг от друга. Определить напряженность электрического поля Е в точке, удаленной от первого заряда на расстояние r1 = 30 см, а от второго – на r2 = 15 см.
Задача № 2 (336). Четыре одинаковых капли ртути, заряженных до потенциала φ = 10 В, сливаются в одну. Каков потенциал φ1 образовавшейся капли?
Задача № 3 (346). Пылинка массой m = 5 нг, несущая на себе N = 10 электронов, прошла в вакууме ускоряющую разность потенциалов U = 1 МВ. Какова кинетическая энергия Т пылинки? Какую скорость v приобрела пылинка?
Задача № 4 (356). Два конденсатора емкостями С1 = 5 мкФ и С2 = 8 мкФ соединены последовательно и присоединены к батарее с ЭДС 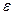 = 80 В. Определить заряды Q1 и Q2 конденсаторов и разности потенциалов U1 и U2 между их обкладками.
= 80 В. Определить заряды Q1 и Q2 конденсаторов и разности потенциалов U1 и U2 между их обкладками.
Задача № 5 (366). Аккумулятор с ЭДС 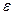 = 12 В заряжается от сети постоянного тока с напряжением U = 15 В. Определить напряжение на клеммах аккумулятора, если его внутреннее сопротивление Ri = 10 Ом.
= 12 В заряжается от сети постоянного тока с напряжением U = 15 В. Определить напряжение на клеммах аккумулятора, если его внутреннее сопротивление Ri = 10 Ом.
| Задача № 6 (406). По двум бесконечно длинным проводам, скрещенным под прямым углом, текут токи I1 и I2 = 2I1 (I1 = 100 А). Определить магнитную индукцию В в точке А, равноудаленной от проводов на расстояние d = 10 см (рисунок). | 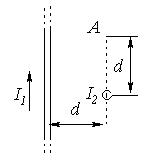 |
Задача № 7 (466). Проволочный виток диаметром D = 5 см и сопротивлением R = 0.002 Ом находится в однородном магнитном поле (В = 0.3 Тл). Плоскость витка составляет угол φ = 40˚ с линиями индукции. Каков заряд Q протечет по витку при выключении магнитного поля?
Задача № 8 (516). На непрозрачную пластину с узкой щелью падает нормально плоская монохроматическая световая волна ( 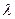 = 600 нм). Угол отклонения лучей, соответствующих второму дифракционному максимуму,
= 600 нм). Угол отклонения лучей, соответствующих второму дифракционному максимуму, 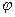 = 20о. Определить ширину d щели.
= 20о. Определить ширину d щели.
Задача № 9 (546). Поток излучения абсолютно черного тела Фе = 10 кВт. Максимум энергии излучения приходится на длину волны λm = 0.8 мкм. Определить площадь S излучающей поверхности.
Вариант 7. (Контрольная работа № 3).
Задача № 1 (307). В вершинах правильного треугольника со стороной а = 10 см находятся заряды Q1 = 10 мкКл, Q2 = 20 мкКл и Q3 = 30 мкКл. Определить силу F, действующую на заряд Q1 со стороны двух других зарядов.
Задача № 2 (337). Тонкий стержень согнут в кольцо радиусом R = 10 см. Он равномерно заряжен с линейной плотностью заряда τ = 80 нКл/м. Определить потенциал φ в точке, расположенной на оси кольца на расстоянии h = 10 см от его центра.
| Задача № 3 (347). Какой минимальной скоростью vmin должен обладать протон, чтобы он мог достигнуть поверхности заряженного до потенциала φ = 400 В металлического шара (рисунок). | 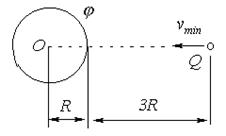 |
Задача № 4 (357). Плоский конденсатор состоит из двух круглых пластин радиусом R = 10 см каждая. Расстояние между пластинами d = 2 мм. Конденсатор присоединен к источнику напряжения U = 80 В. Определить заряд Q и напряженность Е поля конденсатора в двух случаях: а) диэлектрик – воздух; б) диэлектрик – стекло.
Задача № 5 (367). От источника с напряжением U = 800 В необходимо передать потребителю мощность Р =10 кВт на некоторое расстояние. Какое наибольшее сопротивление может иметь линия передачи, чтобы потери энергии в ней не превышали 10 % от передаваемой мощности?
| Задача № 6 (407). По бесконечно длинному проводу, изогнутому так, как это показано на рисунке, течет ток I = 200 А. Определить магнитную индукцию В в точке О. Радиус дуги R = 10 см. | 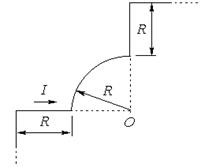 |
Задача № 7 (467). Рамка, содержащая N = 200 витков тонкого провода, может свободно вращается относительно оси, лежащей в плоскости рамки. Площадь рамки S = 50 см2. Ось рамки перпендикулярна линиям индукции однородного магнитного поля (В = 0.05 Тл). Определить максимальную ЭДС 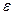 max, которая индуцируется в рамке при ее вращении с частотой n = 40 с-1 .
max, которая индуцируется в рамке при ее вращении с частотой n = 40 с-1 .
Задача № 8 (517). На дифракционную решетку, содержащую n = 100 штрихов на 1 мм, падает нормально монохроматический свет. Зрительная труба спектрометра наведена на максимум второго порядка. Чтобы навести трубу на другой максимум того же порядка, её нужно повернуть на угол 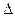
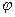 = 16о. Определить длину волны
= 16о. Определить длину волны 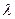 света, падающего на решетку.
света, падающего на решетку.
Задача № 9 (547). Как и во сколько раз изменится поток излучения абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра (λm1 = 780 нм) на фиолетовую (λm2 = 390 нм)?
Вариант 8. (Контрольная работа № 3).
Задача № 1 (308). В вершинах квадрата находятся одинаковые заряды Q1 = Q2 = Q3 = Q4 = 8·10–10 Кл. Какой отрицательный заряд Q нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?
Задача № 2 (338). Поле образовано точечным диполем с электрическим моментом р = 200 пКл·м. Определить разность потенциалов U двух точек поля, расположенных симметрично относительно диполя на его оси на расстоянии r = 40 см от центра диполя.
Задача № 3 (348). В однородное электрическое поле напряженностью Е = 200В/м влетает (вдоль силовой линии) электрон со скоростью vо = 2 Мм/с. Определить расстояние l, которое пройдет электрон до точки, в которой его скорость будет равна половине начальной.
Задача № 4 (358). Два металлических шарика радиусами R1 = 5 см и R2 = 10 см имеют заряды Q1 = 40 нКл и Q2 = -20 нКл соответственно. Найти энергию W, которая выделится при разряде, если шары соединить проводником.
Задача № 5 (368). При включении электромотора в сеть с напряжением U = 220В он потребляет ток I = 5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление R обмотки мотора равно 6 Ом.
Задача № 6 (408). По тонкому кольцу течет ток I = 80 А. Определить магнитную индукцию В в точке А, равноудаленной от точек кольца на расстоянии r = 10 см (рисунок). Угол 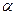 = π/6. = π/6. | 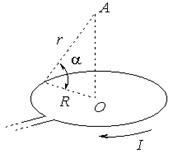 |
Задача № 7 (468). Прямой проводящий стержень длиной l = 40 см находится в однородном магнитном поле (В = 0.1 Тл). Концы стержня замкнуты гибким проводом, находящимся вне поля. Сопротивление всей цепи R = 0.5 Ом. Какая мощность Р потребуется для равномерного перемещения стержня перпендикулярно линиям магнитной индукции со скоростью v = 10 м/с?
Задача № 8 (518). На дифракционную решетку падает нормально монохроматический свет ( 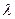 = 410 нм). Угол
= 410 нм). Угол 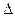
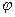 между направлениями на максимумы первого и второго порядка равен 2о21”. Определить число n штрихов на 1 мм дифракционной решетки.
между направлениями на максимумы первого и второго порядка равен 2о21”. Определить число n штрихов на 1 мм дифракционной решетки.
Задача № 9 (548). Определить поглощательную способность ar серого тела, для которого температура, измеренная радиационным пирометром, Трад= 1.4 кК, тогда как истинная температура Т тела равна 3.2 кК.
Вариант 9. (Контрольная работа № 3).
Задача № 1 (309). На расстоянии d = 20 см находятся два точечных заряда: Q1 = -50 нКл и Q2 = 100 нКл. Определить силу F, действующую на заряд Q3 = -10нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.
Задача № 2 (339). Электрическое поле образовано бесконечно длинной заряженной нитью, линейная плотность заряда которой τ = 20 пКл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r1 = 8 см и r2 = 12 см.
| Задача № 3 (349). Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределенным зарядом (τ = 10 нКл/м). Определить кинетическую энергию Т2 электрона в точке 2, если в точке l его кинетическая энергия Т1 = 200 эВ (рисунок). | 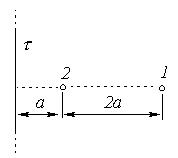 |
Задача № 4 (359). Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика: стекла толщиной d1= 0.2 см и слоем парафина толщиной d2 =0.3 см. Разность потенциалов между обкладками U = 300 В. Определить напряженность Е поля и падение потенциала в каждом из слоев.
Задача № 5 (369). В сеть с напряжением U = 100 В подключили катушку с сопротивлением R1 = 2 кОм и вольтметр, соединенные последовательно. Показание вольтметра U1 = 80 В. Когда катушку заменили другой, вольтметр показал U2 = 60 В. Определить сопротивление R2 другой катушки.
| Задача № 6 (409). По двум бесконечно длинным прямым параллельным проводам текут одинаковые токи I = 60 А. Определить магнитную индукцию В в точке А (рисунок), равноудаленной от проводов на расстояние d = 10 см. Угол β = π/3. | 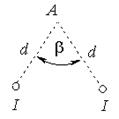 |
Задача № 7 (469). Проволочный контур площадью 500 см2 и сопротивлением 0.1 Ом равномерно вращается в однородном магнитном поле (В = 0.5 Тл). Ось вращения лежит в плоскости кольца и перпендикулярна линиям магнитной индукции. Определить максимальную мощность, необходимую для вращения контура с угловой скоростью ω = 50 рад/с.
Задача № 8 (519). Постоянная дифракционной решетки в n = 4 раза больше длины световой волны монохроматического света, нормально падающего на её поверхность. Определить угол 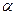 между двумя первыми симметричными дифракционными максимумами.
между двумя первыми симметричными дифракционными максимумами.
Задача № 9 (549). Муфельная печь, потребляющая мощность Р = 1 кВт, имеет отверстие площадью S = 100 см2. Определить долю η мощности, рассеиваемой стенками печи, если температура ее внутренней поверхности равна 1 кК.
Задачи контрольной работы №3 соответствуют заданиям, номера которых указанны в скобках, методического пособия по физике под редакцией Чертова А.Г. (1987г.).
| Контрольная работа № 3. | |||
| Вар. | Физика. Методические указания. Под редакцией Чертова А.Г. (1987г.). | ||
| 1 2 3 4 5 6 7 8 9 | |||
| 310 340 350 | 360 370 410 | 470 520 550 | |
| 301 331 341 | 351 361 401 | 461 511 541 | |
| 302 332 342 | 352 362 402 | 462 512 542 | |
| 303 333 343 | 353 363 403 | 463 513 543 | |
| 304 334 344 | 354 364 404 | 464 514 544 | |
| 305 335 345 | 355 365 405 | 465 515 545 | |
| 306 336 346 | 356 366 406 | 466 516 546 | |
| 307 337 347 | 357 367 407 | 467 517 547 | |
| 308 338 348 | 358 368 408 | 468 518 548 | |
| 309 339 349 | 359 369 409 | 469 519 549 |
Вопросы к экзамену по физике (часть II).
1. Теорема Остроградского - Гаусса для электростатического поля.
2. Напряженность. Работа сил электростатического поля. Потенциал. Связь между потенциалом и напряженностью электростатического поля.
3. Магнитное поле. Закон Био-Савара-Лапласа. Индукция линейного и кругового тока.
4. Действие магнитного поля на проводник с током (закон Ампера) и на движущийся заряд (сила Лоренца).
5. Магнитный поток. Теорема Гаусса для магнитного поля. Явление электромагнитной индукции.
6. Уравнения Максвелла для электро- и магнитостатических полей.
7. Электромагнитные колебания. Колебательный контур. Уравнение свободных незатухающих гармонических колебаний.
8. Электромагнитные колебания. Колебательный контур. Уравнение свободных затухающих гармонических колебаний.
9. Электромагнитные волны. Вектор Умова-Пойнтинга.
10. Волновая теория света. Интерференция и дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракция Френеля на круглом отверстии и на диске.
11. Волновая теория света. Интерференция и дифракция света. Дифракция Фраунгофера на дифракционной решетке.
12. Дисперсия, поглощение и поляризация света. Закон Малюса.
13. Корпускулярная теория света. Фотоэффект и эффект Комптона.
14. Тепловое излучение. Закон Кирхгофа. Закон Стефана-Больцмана. Закон смещения Вина. Квантовая гипотеза Планка.
15. Теория Бора для атома водорода. Постулаты Бора. Спектр атома водорода.
