Уравнение Лиувилля, теорема Лиувилля.
Для функции распределения микросостояний в фазовом пространстве гамильтоновых систем справедливо уравнение Лиувилля:
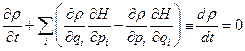 . (1.4.1)
. (1.4.1)
Теорема Лиувилля: функция распределения микроскопических состояний гамильтоновых систем постоянна вдоль фазовых траекторий. То есть для любых двух моментов времени
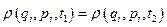 . (1.4.2)
. (1.4.2)
Иногда удобнее пользоваться другой формулировкой этой теоремы. Пусть некоторая совокупность систем ансамбля в момент времени t0 находится в микросостояниях, занимающих объём 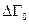 фазового пространства. К моменту времени t изображающие точки перемещаются в объём
фазового пространства. К моменту времени t изображающие точки перемещаются в объём 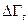 . Из условия сохранения числа систем
. Из условия сохранения числа систем 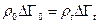 и соотношения (1.4.2) следует, что
и соотношения (1.4.2) следует, что
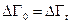 . (1.4.3)
. (1.4.3)
Для гамильтоновых систем фазовый объём произвольной области фазового пространства сохраняется, но может деформироваться, то есть менять свою форму.
1.5. Из теоремы Лиувилля следует, что функция распределения должна выражаться через такие комбинации обобщённых координат и импульсов, которые при движении системы остаются постоянными. Такие величины называют интегралами движения. Интегралов движения много, но аддитивных – семь: энергия, три компоненты вектора импульса, три компоненты вектора момента импульса.
Макроскопическую систему всегда можно рассматривать в такой системе отсчёта, в которой она покоится, и, следовательно, импульс и момент импульса её равны нулю. Остаётся один аддитивный интеграл движения – энергия. Поэтому логарифм функции распределения (аддитивная функция) может зависеть только от энергии:
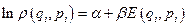 . (1.5.1)
. (1.5.1)
Следовательно, зависимость функции 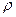 от переменных
от переменных 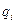 и
и 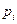 связана только с зависимостью от этих переменных энергии
связана только с зависимостью от этих переменных энергии 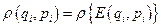 .
.
1.6. Зная функцию распределения можно найти среднее по ансамблю значение физической величины (фазовое среднее):
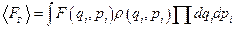 . (1.6.1)
. (1.6.1)
Считается, что временные и фазовые средние равны
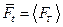 . (1.6.2)
. (1.6.2)
Системы, для которых выполняется это равенство, называются эргодичными.
Для Гиббса представление об ансамбле был удобным вычислительным приёмом для получения средних значений макроскопических величин. Дальнейшие работы по обоснованию статистической физики показали, что понятие ансамбля является более глубоким и важным. Необходимость понятия статистического ансамбля и статистического описания вытекает из свойства динамической неустойчивости движения частиц, а, следовательно, и фазовых траекторий, приводящего к перемешиванию. Неустойчивость проявляется в том, что существуют направления, вдоль которых расстояния между траекториями растут экспоненциально во времени. Очень малое изменение положения фазовой точки, выбранной за начальную, приводит к сильному расхождению соответствующих траекторий. Если движение финитно, то эти траектории не могут разойтись дальше, чем на размер области движения. Поэтому происходит их сильное запутывание, перемешивание. При наличии неустойчивости траектории, имеющие сколь угодно близкие начальные условия, ведут себя совершенно по-разному. Любое малое возмущение будет нарастать и дальнейший маршрут изобразительной точки невозможно предвидеть.
Микросостояние системы характеризуется некоторым набором чисел. Числа задаются с помощью конечного количества знаков, что ограничивает точность описания. Таким образом, состояние системы определяется не точкой в фазовом пространстве (для этого нужна бесконечно большая информация), а небольшой областью. Если фазовые траектории системы имеют сильную зависимость от начальных условий, точки этой области описывают совершенно различные траектории (рис.1).
 |
Таким образом, вместо одной системы и одной фазовой траектории следует рассматривать ансамбль таких систем и ансамбль фазовых траекторий. Понятие ансамбля для систем с перемешиванием появляется естественным образом, потому что для таких систем возможно только статистическое описание. Ансамбль определяют, задавая плотность распределения вероятностей в фазовом пространстве (функцию распределения). Физически это соответствует рассмотрению ансамбля тождественных систем с различными начальными условиями.
Пример.
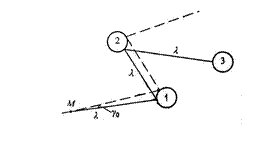
Рассмотрим природу возникновения молекулярного хаоса. Пусть молекула А сталкивается с другими молекулами газа. На рис.2 диски соответствуют поперечному сечению соударений этой молекулы с молекулами 1,2,3. Радиус каждого диска приближённо равен r, средняя длина свободного пробега – 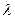 . В какой-то момент времени, который будем считать начальным, скорость молекулы А немного изменяется. На рис.2 сплошной линией изображена невозмущённая траектория молекулы, пунктирной – возмущённая. Она отклонена от невозмущённой на малый угол
. В какой-то момент времени, который будем считать начальным, скорость молекулы А немного изменяется. На рис.2 сплошной линией изображена невозмущённая траектория молекулы, пунктирной – возмущённая. Она отклонена от невозмущённой на малый угол 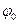 . Легко показать, что после одного соударения, которое считается упругим, угол
. Легко показать, что после одного соударения, которое считается упругим, угол 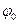 возрастает в
возрастает в 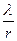 раз. Следовательно после n соударений будем иметь
раз. Следовательно после n соударений будем иметь
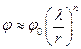 . (1.7.1)
. (1.7.1)
 Для воздуха при нормальном атмосферном давлении длина свободного пробега молекулы газа равна около 10-8 м, а её радиус – 10-10 м. Поэтому
Для воздуха при нормальном атмосферном давлении длина свободного пробега молекулы газа равна около 10-8 м, а её радиус – 10-10 м. Поэтому 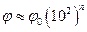 .
.
 Соотношение (1.7.1) обычно записывают иначе. Пусть средняя длина вдоль траектории молекулы будет
Соотношение (1.7.1) обычно записывают иначе. Пусть средняя длина вдоль траектории молекулы будет 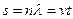 , где v – средняя её скорость и t – время движения. Тогда
, где v – средняя её скорость и t – время движения. Тогда
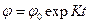 , (1.7.2)
, (1.7.2)
где 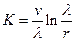 . (
. ( 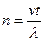 ,
, 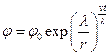 ,
, 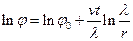 ,
, 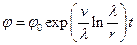 ). Из соотношения (1.7.2) видно, что первоначально как угодно близкие траектории экспоненциально разбегаются, величина k характеризует среднюю скорость их разбегания.
). Из соотношения (1.7.2) видно, что первоначально как угодно близкие траектории экспоненциально разбегаются, величина k характеризует среднюю скорость их разбегания.
Таким образом, траектории молекул газа, которые очень чувствительны к начальным условиям, являются неустойчивыми. Они также чувствительны к возмущениям, вносимым внешним окружением. Можно говорить лишь о вероятности нахождения молекулы в том или ином месте занятого газом объёма. Равновесное макросостояние представляет собой совокупность микросостояний, каждое из которых неустойчиво и через короткое время заменяется другими микросостояниями.
1.8. Учёт квантовых свойств.
Квантовые свойства частиц сначала будем учитывать в квазиклассическом приближении. Это означает:
а) эволюцию микросостояний систем будем описывать фазовыми траекториями. Однако в квазиклассическом приближении считаются возможными только те траектории, которые соответствуют дискретным (квантованным) состояниям.
б) микросостоянию системы соответствует не фазовая точка, а, учитывая соотношение неопределённостей 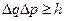 , ячейка размером
, ячейка размером 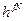 , где f – число степеней свободы, N – число частиц.
, где f – число степеней свободы, N – число частиц.
Число квантовых состояний системы в интервале энергий от Е до 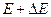 (кратность вырождения):
(кратность вырождения):
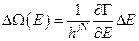 . (1.8.1)
. (1.8.1)
Здесь Г – фазовый объём, соответствующий состояниям с энергией меньшей или равной Е.
Распределения Гиббса.
Конкретный вид функции распределения микросостояний системы зависит от условий, в которых она (система) находится.
а) Микроканоническое распределение Гиббса.
Система изолирована, её энергия Е0 фиксирована. Соответствующий ансамбль называется микроканоническим. Поэтому для системы возможны только такие фазовые траектории, на которых её энергия равна Е0. Вероятность состояний с другими значениями энергий равна нулю. Поскольку в соответствии с теоремой Лиувилля, вдоль фазовых траекторий 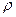 постоянна, то вероятность всех состояний, при которых энергия системы равна Е0, одинакова:
постоянна, то вероятность всех состояний, при которых энергия системы равна Е0, одинакова:
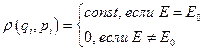 . (1.9.1)
. (1.9.1)
Функция распределения должна удовлетворять условию нормировки. Поэтому 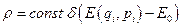 , где
, где 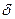 – дельта-функция Дирака (О
– дельта-функция Дирака (О 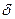 -функции см. пособие «Операторы квантовой механики»).
-функции см. пособие «Операторы квантовой механики»).
Система со строго фиксированной энергией – слишком абстрактная модель. В природе не существует совершенно изолированных систем. Взаимодействие с внешней средой, хотя и очень слабое, всегда есть. В квантовой механике энергия точно определена ( 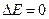 ), если время жизни данного состояния системы бесконечно (
), если время жизни данного состояния системы бесконечно ( 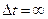 ). Поэтому обычно значение энергии системы указывают в узком интервале (
). Поэтому обычно значение энергии системы указывают в узком интервале ( 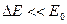 ).
).
Макросостоянию системы соответствует большое число микросостояний (допустимых квантовых состояний). Поскольку все микросостояния для изолированной системы равновероятны, вероятность того, что изолированная система находится в определённом макросостоянии, пропорциональна числу совместимых с ним микросостояний (по формуле сложения вероятностей). Поэтому микроканоническое распределение Гиббса можно записать так:
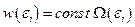 . (1.9.2)
. (1.9.2)
б) Каноническое распределение Гиббса.
Подсистема находится в термодинамическом равновесии с термостатом. Термостатом называется система, температура которой при взаимодействии с подсистемой остаётся постоянной. Соответствующий ансамбль называется каноническим. Каноническое распределение Гиббса можно получить, если рассматривать подсистему с термостатом как одну изолированную систему и применить к ней микроканоническое распределение. При этом должны выполнятся условия:
1) 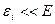 (Е – энергия изолированной системы);
(Е – энергия изолированной системы);
2) 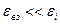 (
( 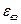 – энергия взаимодействия подсистемы и термостата);
– энергия взаимодействия подсистемы и термостата);
3) обмен частицами между подсистемой и термостатом отсутствует, число частиц в подсистеме постоянно.
Каноническое распределение Гиббса в квазиклассическом приближении можно записать в виде:
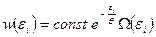 (1.9.3).
(1.9.3).
Здесь 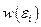 – вероятность того, что подсистема, составляющая малую часть изолированной системы, находится в одном из состояний
– вероятность того, что подсистема, составляющая малую часть изолированной системы, находится в одном из состояний 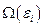 с энергией
с энергией 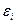 ; параметр
; параметр
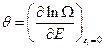 (1.9.4)
(1.9.4)
называют модулем канонического распределения. Величина
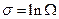 (1.9.5)
(1.9.5)
есть энтропия. Здесь энтропия определена для равновесного состояния. Связь статистической энтропии 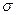 и термодинамической S:
и термодинамической S:
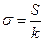 . (1.9.6)
. (1.9.6)
Постоянная k называется постоянной Больцмана ( 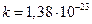 Дж/К). Если число микросостояний
Дж/К). Если число микросостояний 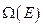 интерпретировать как меру неточности знаний о системе или как меру хаотичности, то энтропию также можно считать мерой хаотичности.
интерпретировать как меру неточности знаний о системе или как меру хаотичности, то энтропию также можно считать мерой хаотичности.
Свойства модуля канонического распределения:
1)  является положительной величиной;
является положительной величиной;
2) эта величина может относиться только к макросистемам;
3) равенство модулей подсистем является условием их теплового равновесия.
Поэтому величину  называют статистической температурой:
называют статистической температурой:
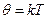 . (1.9.7)
. (1.9.7)
Из условия нормировки 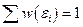 следует:
следует:
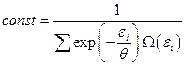 . (1.9.8)
. (1.9.8)
Выражение
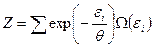 (1.9.9)
(1.9.9)
называется статистической суммой или суммой по состояниям. Подставляя значение постоянной в выражение (1.9.3) получаем
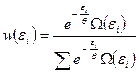 . (1.9.10)
. (1.9.10)
Из формул (1.9.3) и (1.9.10) следует, что в каноническом ансамбле энергия подсистемы, состоящей из большого числа частиц, определяется достаточно точно: распределение имеет резкий максимум при некотором значении энергии 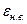 (наиболее вероятном значении энергии). В распределении есть экспоненциально убывающий множитель
(наиболее вероятном значении энергии). В распределении есть экспоненциально убывающий множитель 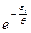 , однако число состояний
, однако число состояний 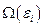 для систем с большим числом частиц быстро растёт с энергией подсистемы. Например, если подсистемой является газ, состоящий из N одинаковых молекул, заключённых в сосуде, то
для систем с большим числом частиц быстро растёт с энергией подсистемы. Например, если подсистемой является газ, состоящий из N одинаковых молекул, заключённых в сосуде, то 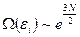 . Произведение двух функций, зависящих от энергий: быстро убывающей и быстро возрастающей, приводит к возникновению у распределения Гиббса резкого максимума (рис.3).
. Произведение двух функций, зависящих от энергий: быстро убывающей и быстро возрастающей, приводит к возникновению у распределения Гиббса резкого максимума (рис.3).
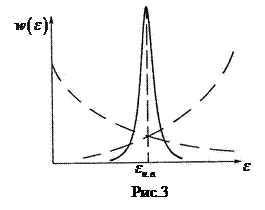
Подавляющую часть времени подсистема будет проводить в состояниях с энергией близкой к 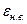 .
.
Для макроскопической подсистемы
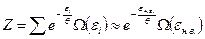 . (1.9.11)
. (1.9.11)
Наиболее вероятное состояние вносит основную долю в среднее значение величин, характеризующих подсистему. Например, для энергии имеем: 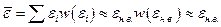 . (Принимаем
. (Принимаем 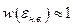 . Соотношение (1.9.6) теперь можно переписать точнее:
. Соотношение (1.9.6) теперь можно переписать точнее:
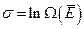 . (1.9.12)
. (1.9.12)
То есть энтропия макроскопической системы равна логарифму числа состояний системы, находящейся в состоянии равновесия.
Выразим также статистическую сумму через среднюю энергию подсистемы:
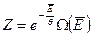 . (1.9.13)
. (1.9.13)
Каноническое распределение Гиббса в классическом приближении:
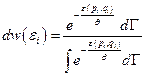 , (1.9.14)
, (1.9.14)
где 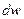 – вероятность того, что микросостояние системы изображается одной из точек, находящихся в элементе фазового объёма
– вероятность того, что микросостояние системы изображается одной из точек, находящихся в элементе фазового объёма 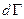 , соответствующего интервалу энергий подсистемы от
, соответствующего интервалу энергий подсистемы от 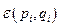 до
до 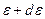 . Соответствующая функция распределения:
. Соответствующая функция распределения:
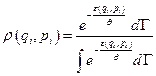 , (1.9.15)
, (1.9.15)
где 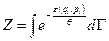 – статистический интеграл.
– статистический интеграл.
в) Большое каноническое распределение Гиббса.
Подсистема обменивается с окружением (термостатом) не только энергией, но и частицами. Энергия подсистемы – 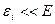 , число частиц подсистемы –
, число частиц подсистемы – 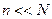 . Е и N – энергия и число частиц изолированной системы, состоящей из подсистемы и термостата. Распределение вероятностей называют большим каноническим распределением:
. Е и N – энергия и число частиц изолированной системы, состоящей из подсистемы и термостата. Распределение вероятностей называют большим каноническим распределением:
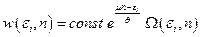 (1.9.16).
(1.9.16).
Из условия нормировки следует
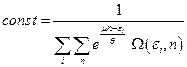 . (1.9.17)
. (1.9.17)
Физический смысл величины 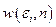 : она определяет вероятность того, что подсистема находится в одном из состояний
: она определяет вероятность того, что подсистема находится в одном из состояний 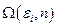 с энергией
с энергией 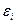 и числом частиц n. Буквой
и числом частиц n. Буквой  по-прежнему обозначена статистическая температура. Величина
по-прежнему обозначена статистическая температура. Величина
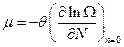 (1.9.18)
(1.9.18)
(производная берётся при постоянном значении энергии) называется химическим потенциалом. Как и температура, химический потенциал может относится только к макроскопическим системам. Равенство химических потенциалов является условием равновесия макросистем, которые могут обмениваться между собой частицами. Физический смысл химического потенциала: он определяет изменение энергии системы при изменении числа частиц на единицу (при фиксированных энтропии и объёме).
Примеры решения задач.
1. Определить фазовую траекторию линейного гармонического осциллятора с энергией 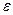 и вычислить фазовый объём, который ограничен гиперповерхностью энергии (поверхностью постоянной энергии).
и вычислить фазовый объём, который ограничен гиперповерхностью энергии (поверхностью постоянной энергии).
Гармонический осциллятор – это материальная точка, которая совершает периодическое колебательное движение около положения устойчивого равновесия. Линейный гармонический осциллятор имеет одну степень свободы, то есть f=1, N=1. Следовательно, его фазовое пространство имеет 2fN=2 измерения.
Из уравнений Гамильтона 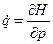 ,
, 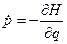 , где
, где 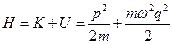 , находим
, находим 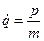 (10.1),
(10.1), 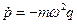 (10.2). Из уравнения (10.1) следует, что
(10.2). Из уравнения (10.1) следует, что 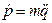 , поэтому получаем
, поэтому получаем 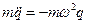 или
или 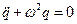 . Решение данного дифференциального уравнения есть
. Решение данного дифференциального уравнения есть 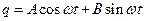 (10.3).
(10.3).
Постоянные А и В находят из начальных условий. Если в начальный момент времени осциллятор находится в начале координат, то есть при 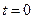 ,
, 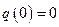 , значит
, значит 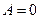 . Тогда решением уравнения (10.3) будет выражение
. Тогда решением уравнения (10.3) будет выражение 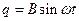 (10.4), где
(10.4), где 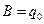 – амплитуда колебаний. Для импульса частички получаем
– амплитуда колебаний. Для импульса частички получаем 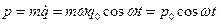 (10.5), где
(10.5), где 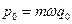 .
.
Соотношение (10.4) и (10.5) являются уравнением эллипса в параметрическом виде
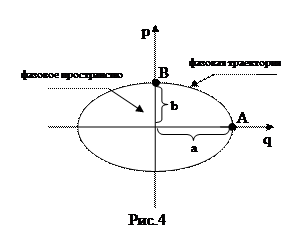
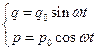 .
.
Исключая время 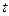 из уравнений
из уравнений 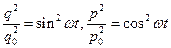 получаем уравнение эллипса:
получаем уравнение эллипса: 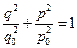 . Таким образом при колебании осциллятора точка, которая изображает состояние системы, в фазовом пространстве описывает эллипс. Поэтому, фазовый объём
. Таким образом при колебании осциллятора точка, которая изображает состояние системы, в фазовом пространстве описывает эллипс. Поэтому, фазовый объём 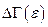 , который ограничен поверхностью постоянной энергии, в данном случае есть площадь эллипса
, который ограничен поверхностью постоянной энергии, в данном случае есть площадь эллипса 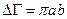 .
.
Когда осциллятор находится в состоянии, которое изображается т.А на рис.4, его кинетическая энергия равняется нулю. Поэтому, 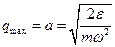 . Когда осциллятор находится в состоянии соответствующей т.В, его потенциальная энергия равняется нулю, потому
. Когда осциллятор находится в состоянии соответствующей т.В, его потенциальная энергия равняется нулю, потому 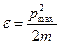 . Откуда
. Откуда 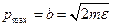 .
.
Следовательно, площадь эллипса, то есть фазовый объём 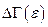 будет равняться:
будет равняться: 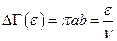 .
.
2. 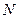 частиц идеального газа заключены в объёме
частиц идеального газа заключены в объёме 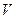 и подчиняются микроканоническому распределению с энергией
и подчиняются микроканоническому распределению с энергией 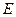 . Вычислить для этой системы фазовый объём
. Вычислить для этой системы фазовый объём 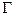 , энтропию
, энтропию  и температуру
и температуру 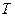 .
.
Энергия Е идеального газа зависит лишь от обобщённых импульсов. Поэтому фазовый объём 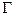 будет равняться:
будет равняться:
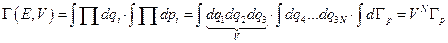 , где
, где 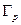 – объём 3N-мерного шара в пространстве импульсов, определяемый энергией Е. Из курса геометрии известно, что объём шара в 3-х мерном пространстве определяется по формуле
– объём 3N-мерного шара в пространстве импульсов, определяемый энергией Е. Из курса геометрии известно, что объём шара в 3-х мерном пространстве определяется по формуле 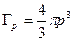 . В импульсном пространстве 3N измерений
. В импульсном пространстве 3N измерений 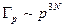 . Учитывая, что
. Учитывая, что 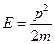 (откуда
(откуда 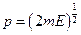 ), получаем
), получаем 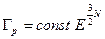 . Значит, фазовый объём будет равняться
. Значит, фазовый объём будет равняться 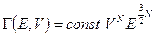 . Находим энтропию S.
. Находим энтропию S. 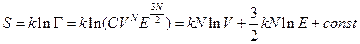 . Определяем температуру Т.
. Определяем температуру Т.
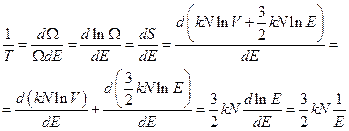 .
.
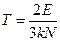 .
.
Вопросы для самопроверки.
1. Объяснить феноменологический и статистический методы изучения макроскопических систем.
2. Какими величинами характеризуются макроскопическое и микроскопическое состояния газа?
3. Что характеризует фазовая траектория?
4. Что называется фазовым пространством? Для чего вводится это понятие?
5. Для какой системы фазовое пространство допускает наглядное изображение в реальном трехмерном пространстве?
6. Как найти среднее значение физической величины за определённый, достаточно большой промежуток времени Т?
7. Что называется статистическим ансамблем системы?
8. Что называется элементом фазового объёма?
9. Физический смысл плотности распределения микроскопических состояний систем ансамбля (функции распределения)?
10. Свойства функции распределения.
11. Сформулировать теорему Лиувилля, написать уравнение Лиувилля.
12. В чём заключается идея Гиббса?
13. В чём проявляется неустойчивость движения частиц, неустойчивость фазовых траекторий?
14. Каковы свойства системы, заключённой в объёме V, траектории частиц которой неустойчивы?
15. Какие квантовые свойства частиц учитывают в квазиклассическом приближении?
16. Записать микроканоническое, каноническое распределения Гиббса.
17. Физический смысл модуля  канонического распределения Гиббса.
канонического распределения Гиббса.
18. Записать каноническое распределение Гиббса в классическом приближении. Условие применимости.
19. Что называется статистической суммой, суммой по состояниям?
20. Записать большое каноническое распределение Гиббса.
21. Физический смысл химического потенциала 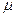 большого канонического распределения Гиббса.
большого канонического распределения Гиббса.
22. Доказать, что энтропия – аддитивная величина.
Задачи.
1. Определить фазовую траекторию для частицы массой 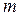 , движущейся по инерции со скоростью
, движущейся по инерции со скоростью 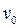 , проиллюстрировать справедливость теоремы Лиувилля.
, проиллюстрировать справедливость теоремы Лиувилля.
2. Начертить фазовые траектории одномерного движения материальных точек в поле силы тяжести с ускорением 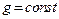 и проиллюстрировать справедливость теоремы Лиувилля.
и проиллюстрировать справедливость теоремы Лиувилля.
3. Проверить справедливость теоремы Лиувилля точек массой m, движущихся по инерции вдоль некоторого направления.
4. Определить фазовую траекторию для свободной частицы массой 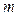 при наличии силы трения, пропорциональной её скорости. (Уравнение движения частицы
при наличии силы трения, пропорциональной её скорости. (Уравнение движения частицы 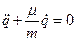 ).
).
5. Определить фазовую траекторию для линейного осциллятора с малым трением. (Уравнение движения линейного осциллятора 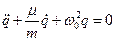 ).
).
6. Вычислить фазовый объём 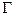 для релятивистской частицы с массой
для релятивистской частицы с массой 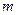 , движущейся в объёме
, движущейся в объёме 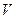 и обладающей энергией
и обладающей энергией 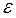 .
.
7. Для 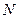 невзаимодействующих линейных осцилляторов с энергией
невзаимодействующих линейных осцилляторов с энергией 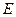 справедливо микроканоническое распределение. Вычислить для этой системы фазовый объём
справедливо микроканоническое распределение. Вычислить для этой системы фазовый объём 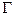 , энтропию
, энтропию  и температуру
и температуру 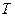 .
.
8. Записать в классическом приближении распределение Гиббса по энергиям для линейного гармонического осциллятора и вычислить среднее значение его энергии.
9. Вывести каноническое распределение Гиббса из общей формулы микроканонического распределения, считая, что в качестве термостата выступает: 1) совокупность 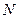 линейных осцилляторов; 2) совокупность
линейных осцилляторов; 2) совокупность 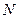 частиц идеального газа. При выводе считать, что отношение
частиц идеального газа. При выводе считать, что отношение 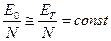 при
при 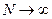 , где
, где 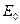 и
и 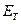 – энергия замкнутой системы и энергия термостата соответственно. Показать, что окончательный результат не зависит от выбора термостата.
– энергия замкнутой системы и энергия термостата соответственно. Показать, что окончательный результат не зависит от выбора термостата.
10. Идеальный газ, состоящий из 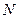 частиц, находится в термостате с температурой
частиц, находится в термостате с температурой 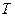 . Найти вероятность того, что газ имеет заданное значение энергии
. Найти вероятность того, что газ имеет заданное значение энергии 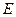 из интервала
из интервала 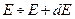 .
.
11. Показать, что каноническое распределение Гиббса для систем с очень большим числом частиц ( 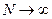 ) переходит в микроканоническое.
) переходит в микроканоническое.
12. Показать, что для системы с большим числом 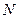 невзаимодействующих частиц наивероятнейшая энергия
невзаимодействующих частиц наивероятнейшая энергия 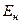 совпадает со средней энергией системы.
совпадает со средней энергией системы.
13. Для линейного гармонического осциллятора с энергией 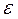 вычислить фазовый объём
вычислить фазовый объём 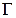 , ограниченный гиперповерхностью энергии. Оценить объём элементарной фазовой ячейки, используя формулу энергетического спектра
, ограниченный гиперповерхностью энергии. Оценить объём элементарной фазовой ячейки, используя формулу энергетического спектра 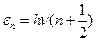 ,
, 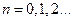 .
.
14. Найти число микросостояний 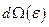 с энергией
с энергией 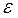 в интервале
в интервале 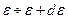 для частицы газа, энергия которой связана с импульсом соотношением
для частицы газа, энергия которой связана с импульсом соотношением 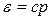 , где
, где 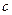 – скорость света в вакууме.
– скорость света в вакууме.
