Свойства определенного интеграла, выражаемые неравенствами

Теорема 4. Пусть 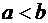, функции 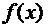и и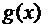нтегрируемы на промежутке 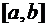и при всех 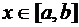справедливо неравенство

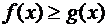. (11)

Тогда

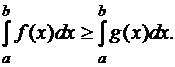(12)

Доказательство. Рассмотрим разность интересующих нас интегралов как интеграл разности данных функций. В силу (9)

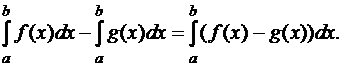
Последний интеграл запишем по формуле (4), т.е. следуя определению определённого интеграла. Тогда получим

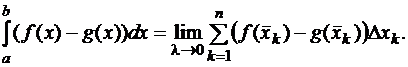
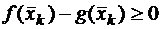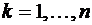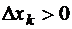Здесь все парные произведения интегральной суммы неотрицательны. Действительно, по условию (11) при всех , а при всех 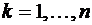, поскольку .

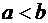Значит и сама интегральная сумма неотрицательна. Тогда по теореме о предельном переходе в неравенстве неотрицателен и ее предел. Таким образом, получаем:

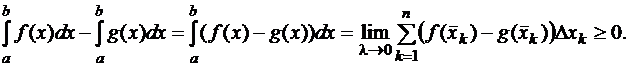
Теорема доказана.

Следствие. Пусть 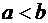, функция 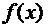интегрируема на промежутке 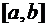и при всех 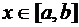справедливо неравенство 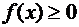. Тогда .

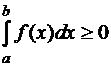Теорема 5. Если функция 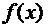интегрируема на промежутке 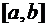, то функция 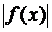также интегрируема на промежутке 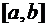и при 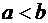справедливо неравенство

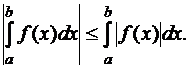(13)

Доказательство. Проведем его только для непрерывных функций. Заметим, что

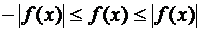(14)

для всех 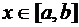. К цепочке неравенств (14) применим теорему 4. Получим

,

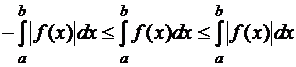Что равносильно неравенству (13).

Теорема о среднем значении

Теорема 6. Пусть функци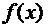и и 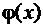непрерывны на промежутке 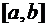и пусть функция 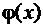не меняет знака на этом промежутке. Тогда найдется такая точка 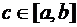, что справедливо равенство

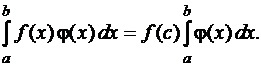(15)

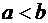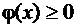Доказательство. Без ограничения общности будем считать, что , а при 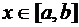. Рассмотрим два случая.

1). Пусть 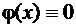при всех 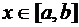. Тогда равенство (15) выполнено очевидным образом.

2). Пусть 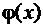не является тождественно равной нулю. Тогда в силу непрерывности функции 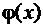можем утверждать, что

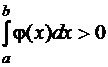
Поскольку функция 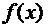непрерывна на замкнутом промежутке 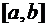, то она достигает на этом промежутке своего наибольшего значения 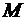и своего наименьшего значения 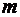, т.е. при всех 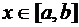справедливы неравенства

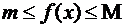. (16)

Домножим неравенства (16) на положительные значения функции 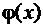и получим справедливые при всех 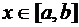неравенства

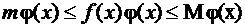(17)

К цепочке неравенств (17) применим теорему 4 и получим справедливые неравенства

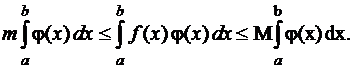(18)

Разделим все части цепочки неравенств (18) на положительное число 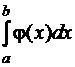. Получим

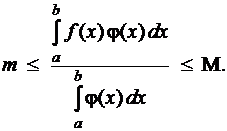
Поскольку непрерывная функция 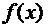принимает на промежутке 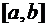все значения между своим наибольшим 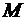и наименьшим 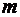, существует такая точка 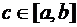, что

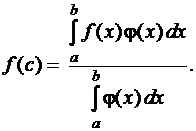
Отсюда следует, что

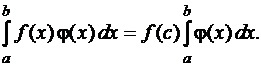
Таким образом, теорема 6 доказана.

Следствие. Если функция 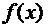непрерывна на промежутке 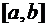, то можно указать такое значение 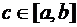, что

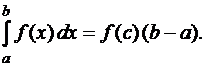(19)

Доказательство. Будем считать 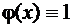при 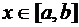. Тогда согласно теореме 6 найдется такая точка 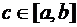, что

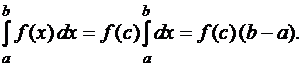
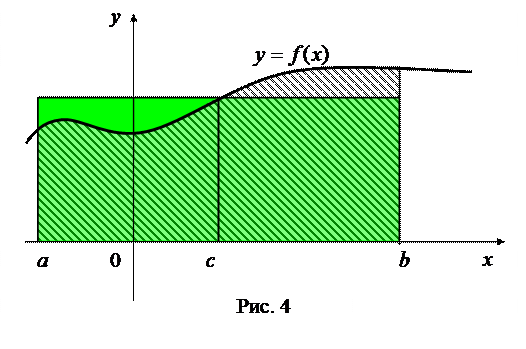
В случае, когда 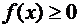при всех 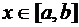, формула (19) имеет простой геометрический смысл. Рассмотрим криволинейную трапецию, ограниченную линиями 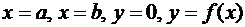. Согласно равенству(19) площадь этой криволинейной трапеции равна площади прямоугольника с основанием 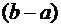и высотой 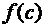(рис. 4).

Теорема Барроу

Рассмотрим определенный интеграл с переменным верхним пределом

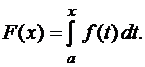(20)

Здесь 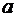– число, 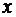– переменная. Таким образом, 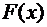является функцией верхнего предела .

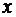В силу геометрического смысла определённого интеграла, если 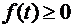, , 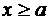то величина 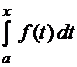является площадью криволинейной трапеции, ограниченной справа прямой 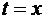. Т.к. 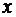– переменная, то и интеграл (20) изображает трапецию с переменной площадью (рис. 5).

Справедливо следующее важное утверждение.

Теорема Барроу. Если функция 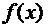непрерывна, то

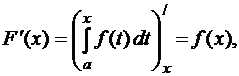
т.е. производная определенного интеграла по переменному верхнему пределу равна значению подынтегральной функции в точке дифференцирования.

Доказательство. По определению производной

,

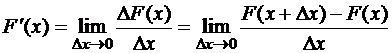где

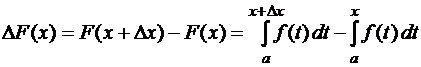. (21)

Во втором слагаемом правой части (21) поменяем пределы интегрирования по формуле (6) и на основании теоремы 3 получим:

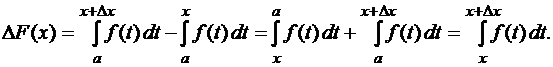
Величина 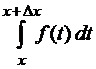является площадью заштрихованной криволинейной трапеции (рис. 5). Поскольку функция 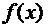непрерывна, по теореме 6 о среднем значении найдется такая точка 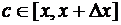, для которой справедливо

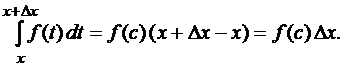
Тогда

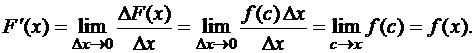
Теорема доказана.

Приведем примеры применения теоремы Барроу.

Пример 6.1.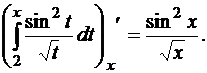

Пример 6.2.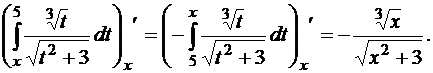

Пример 6.3. 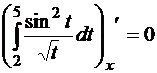,т.к. определенный интеграл с постоянными пределами – это постоянная величина.

Пример 6.4. 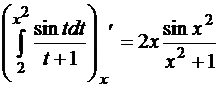. Здесь мы имеем дело со сложной функцией: 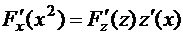, где , .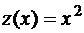

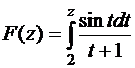Следствие. Любая непрерывная на промежутке 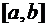функция имеет на этом промежутке первообразную.

Действительно, если 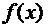– непрерывна, то существует 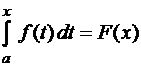. Но по теореме Барроу 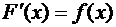, т.е. 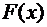– первообразная для 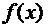. Таким образом, 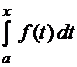– первообразная для .

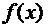Замечание. Первообразная непрерывной функции не всегда может быть выражена в терминах элементарных функций.