Механические приложения определенного интеграла
Пусть имеется материальная точка 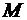 массой
массой 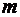 . Зададим ось
. Зададим ось 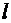 .
.
Моментом инерцииточки 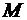 относительно оси
относительно оси 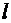 называется произведение её массы на квадрат расстояния до оси:
называется произведение её массы на квадрат расстояния до оси:
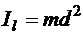
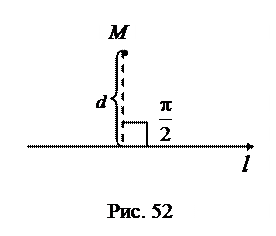
(рис. 52).
Статическим моментом точки 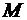 относительно оси
относительно оси 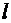 называется произведение её массы на расстояние от точки до оси, взятое с каким-либо знаком:
называется произведение её массы на расстояние от точки до оси, взятое с каким-либо знаком:
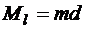
или

в зависимости от договорённости, с какой стороны оси 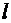 материальным точкам приписывается положительный статический момент, а с какой – отрицательный.
материальным точкам приписывается положительный статический момент, а с какой – отрицательный.
Пусть задана система, состоящая из конечного числа 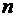 материальных точек
материальных точек 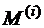 с массами
с массами 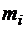 , отстоящих от оси
, отстоящих от оси 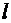 на расстоянии
на расстоянии 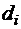 . Тогда
. Тогда
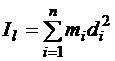 ,
,
а
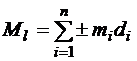 , (67)
, (67)
причём в формуле (67) для точек, расположенных по разные стороны от оси 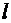 , выбираются разные знаки.
, выбираются разные знаки.
Пусть теперь масса сплошным образом распределена по плоской пластине. Тогда вместо сумм рассматривают интегралы. Будем считать, что масса распределена по плоской фигуре равномерно. Для простоты считаем плотность распределения массы равной единице. Тогда масса любой части фигуры равна её площади.
Рассмотрим две показательные задачи.
1.Найти статический момент 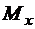 и момент инерции
и момент инерции 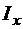 прямоугольника с основанием
прямоугольника с основанием 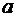 и высотой
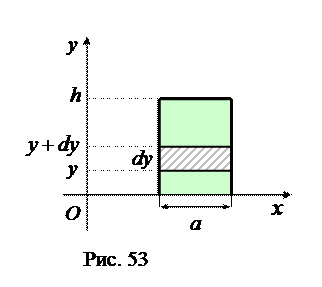
и высотой 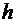 относительно его основания (рис. 53).
относительно его основания (рис. 53).
Выделим внутри прямоугольника полоску высотой 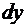 и шириной
и шириной 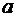 . Расстояние этой полоски до оси
. Расстояние этой полоски до оси 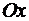 равно
равно 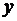 ,
, 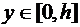 . Масса выделенного элемента равна его площади
. Масса выделенного элемента равна его площади 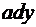 . Вычислим статический момент и момент инерции выделенного элемента относительно оси
. Вычислим статический момент и момент инерции выделенного элемента относительно оси 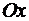 :
: 
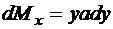 ,
,
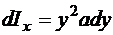 .
.
Тогда
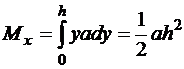 , (68)
, (68)
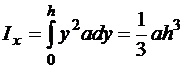 . (69)
. (69)
2.Найти статические моменты 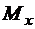 ,
, 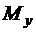 и моменты инерции
и моменты инерции 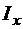 ,
, 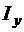 криволинейной трапеции, ограниченной линиями
криволинейной трапеции, ограниченной линиями 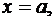
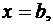
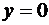 ,
, 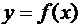 , относительно координатных осей.
, относительно координатных осей.
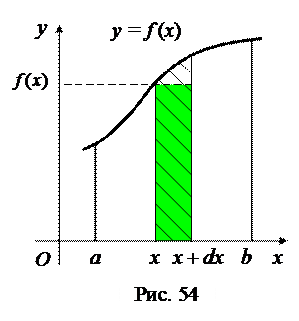
А. Ищем моменты относительно оси 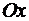 (рис. 54). Выделим внутри трапеции криволинейную полоску, опирающуюся на отрезок
(рис. 54). Выделим внутри трапеции криволинейную полоску, опирающуюся на отрезок 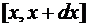 . Будем вычислять бесконечно малые элементы моментов по формулам (68), (69) как моменты прямоугольной полоски с основанием
. Будем вычислять бесконечно малые элементы моментов по формулам (68), (69) как моменты прямоугольной полоски с основанием 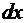 и переменной высотой
и переменной высотой 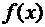 . Тогда
. Тогда
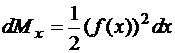 , (70)
, (70)
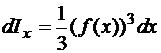 . (71)
. (71)
В формулах (70), (71) мы, пренебрегая бесконечно малыми величинами более высокого порядка малости, чем dx, отождествили криволинейную полоску с прямоугольником высоты 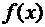 . Проинтегрируем полученные равенства при изменении
. Проинтегрируем полученные равенства при изменении 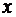 от
от 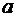 до
до 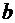 и получим
и получим
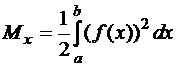 , (72)
, (72)
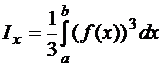 . (73)
. (73)
Б. Ищем статический момент и момент инерции относительно оси 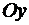 (рис. 55). Выделим внутри трапеции ту же полоску, что и в п. А. За бесконечно малый элемент массы этой полоски примем массу прямоугольника с основанием
(рис. 55). Выделим внутри трапеции ту же полоску, что и в п. А. За бесконечно малый элемент массы этой полоски примем массу прямоугольника с основанием 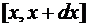 и высотой
и высотой 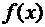 . В силу сделанного ранее предположения масса этого прямоугольника равна его площади. Расстояние любой точки этого прямоугольника до оси
. В силу сделанного ранее предположения масса этого прямоугольника равна его площади. Расстояние любой точки этого прямоугольника до оси 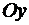 равно
равно 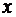 . Тогда
. Тогда
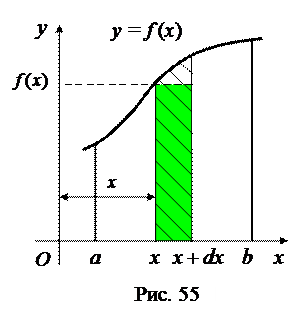
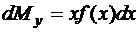 , (74)
, (74)
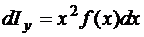 . (75)
. (75)
Интегрируем равенства (74), (75) при изменении переменной 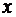 от
от 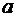 до
до 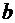 и получим
и получим
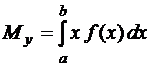 , (76)
, (76)
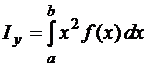 . (77)
. (77)
Знание статических моментов плоской фигуры относительно координатных осей позволяет определить координаты центра тяжести этой фигуры.
Известно, что величина статических моментов не изменится, если предположить, что вся масса фигуры сосредоточена в центре тяжести этой фигуры.
Пусть 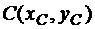 – центр тяжести фигуры массой
– центр тяжести фигуры массой 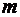 , а
, а 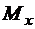 ,
, 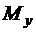 – её статические моменты относительно координатных осей. Тогда
– её статические моменты относительно координатных осей. Тогда
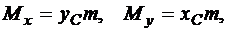
откуда
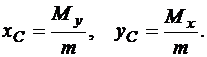 (78)
(78)
