Уравнение неразрывности потока.
Условие неразрывности потока основывается на законе сохранения вещества.
А также на следующих допущениях:
а) трубка тока имеет свойство непроницаемости для внешних, обтекающих ее потоков;
б) предположение о сплошности (неразрывности) среды для установившегося течения несжимаемой жидкости.
На этих основаниях можно утверждать, что объемный расход во всех сечениях элементарной струйки (см. рис.5.2) один и тот же.
Уравнение неразрывности для элементарной струйки (уравнение расхода для элементарной струйки).
δQ = V1 *δS1 = V2 *δS2→ const (вдоль струйки). (5.6)
Уравнениенеразрывностидля потока, ограниченного непроницаемыми стенками (уравнение расхода для потока).
Q = Vср1 *S1 = Vср2 *S2→ const (вдоль потока), (5.6’)
где Vср1 , Vср2 - средние скорости.
Из этого уравнения (5.6') следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям сечений:
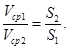
Уравнение расхода (5.6‘) является следствием общего закона сохранения вещества приусловии сплошности (неразрывности) течения.
Уравнение Бернулли для элементарной струйки
Идеальной жидкости
Установившееся течение идеальной жидкости происходит под действием одной массовой силы — силы тяжести. Для этого случая основное уравнение установившегося течения идеальной жидкости связывает между собой давление в жидкости и скорость ее течения.
Возьмем одну из элементарных струек, составляющих поток, выделим сечениями 1и 2участок этой струйки произвольной длины (рис.5.3). Пусть площадь первого сечения равна δS1, скорость в нем V1 , давление P1, а высота от плоскости сравнения Z1. Во втором сечении δS2, V2 , P2 и Z2.
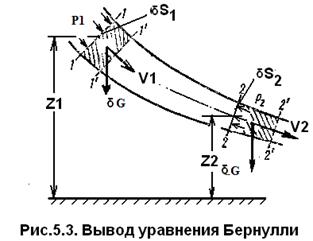
За бесконечно малый отрезок времени δt выделенный участок струйки переместится в положение 1’ – 2’.
Применим к массе жидкости в объеме участка струйки теорему о кинетической энергии: работа сил, приложенных к телу, равна приращению кинетической энергии этого тела.
На жидкость действуют силы тяжести и силы давления, нормальные к поверхностям сечений рассматриваемого участка струйки.
Используя формулировку теоремы, подсчитаем работу сил давления, сил тяжести и изменение кинетической энергии участка струйки за время δt:
(mV22)/2 - (m V12)/2 = G*( Z2- Z1) = G*h
Работа силы давления в первом сечении положительна, так как направление силы совпадает с направлением перемещения, и выражается как произведение силы p1*δS на путь V1δt:
(p1*δS1)*(V1δt)
Работа силы давления во втором сечении имеет знак минус, так как направление силы противоположно направлению перемещения, и определяется выражением
- (p2*δS2) *(V2δt).
Силы давления, действующие по поверхности струйки, работы не производят, так как они нормальны к перемещениям.
Работа сил давления равна
δA = (p1*δS1) *( V1δt)— (p2*δS2) *(V2δt). (5.7)
Работа силы тяжести равна изменению потенциальной энергиивыделенного объема струйки. Из потенциальной энергии жидкости в объеме 1 - 2 вычтем потенциальную энергию жидкости в объеме 1’- 2’. При этом энергия промежуточного объема 1’- 2 сократится, и останется лишь разность энергии элементов 1- 1’, 2- 2’.
По уравнению расходов (закон неразрывности) (5.6’) объемы и силы тяжести заштрихованных элементов 1 -1’ и 2 - 2’ равны между собой:
δG = ρ*g* V1*δS1*δt = ρ*g* V2*δS2*δt . (5.8)
Тогда работа силы тяжести выразится как произведение разности высот на силу тяжести δG:
(z1-z2) *δG. (5.9)
Чтобы подсчитать приращение кинетической энергии рассматриваемого участка струйки за время δt, необходимо из кинетической энергии объема 1’- 2’ вычесть кинетическую энергию объема 1 - 2. При вычитании кинетическая энергия промежуточного объема 1’ - 2 сократится, и останется лишь разность кинетических энергий элементов 2 — 2’ и 1 - 1’, масса каждого из которых равна δG/g.
Таким образом, приращение кинетической энергии на участке струйки равно
(V22- V12)* δG/(2g), (5.10)
Сложив работу сил давления (см. уравнение 5.7) с работой силы тяжести (5.9) и приравняв эту сумму приращению кинетической энергии (5.10), получим исходное уравнение для трех видов уравнения Бернулли.
(p1*δS1) *( V1δt)— (p2*δS2) *( V2δt) +(z1-z2) *δG=(V22- V21)* δG/(2g). (5.11).
сохранять на доске!
