Предельный признак сравнения.

Предельный признак сравнения.

Пусть имеем два ряда с положительными членами

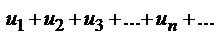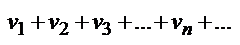(1) и (2), для которых выполняется условие: 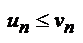. Тогда из сходимости ряда 2 следует сходимость ряда 1;

из расходимости ряда 1 следует расходимость ряда 2.

Предельный признак сравнения.

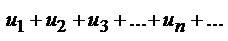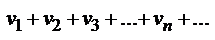Имеем два ряда (1) и (2).

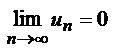. Если L существует, то оба ряда сходятся одновременно.

Пусть ряд 2 сходится, тогда по обычному признаку сравнения сходится и ряд 1.

Имеем ряд :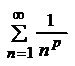

1) 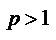ряд сходится

2) 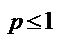ряд расходится.

Признак Даламера

Если в ряду с положительными членами 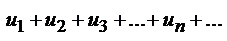отношение (n + 1)-го члена к n-му при имеет конечный предел l, то есть 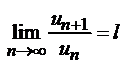, то

ряд сходится в случае ;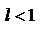

ряд расходится в случае ;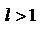

3) в случае 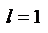ответа о сходимости или расходимости ряда теорема не дает.

Обобщеный признак Коши.

Если для ряда с положительными членами 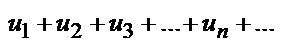величина 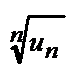имеет конечный предел l при 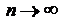, то есть 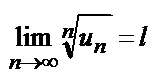, то

в случае 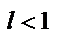ряд сходится;

в случае 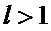ряд расходится;

3) в случае 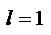ответа о сходимости или расходимости ряда теорема не дает.

Интегральный признак Коши.

Пусть члены ряда положительны и не возрастают, то есть 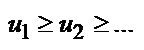и пусть f(х) – такая непрерывная не возрастающая функция, что , , .

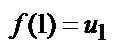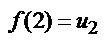Тогда справедливы следующие утверждения:

если несобственный интеграл 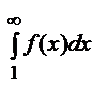сходится, то сходится и исходный ряд;

если указанный интеграл расходится, то расходится и исходный ряд.

Знакопеременные ряды, признак Лейбница.

Ряд называется знакопеременны , если среди его членов имеются как +, так и -.

Теорема1. Если знакопеременный ряд таков, что ряд, составленный из абсолютных величин его членов 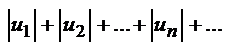сходится, то и данный знакопеременный ряд также сходится.

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов расходится, то данный ряд называется условно или не абсолютно сходящимся рядом.

Теорема Лейбница: Если в знакочередующемся ряду 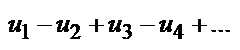, где 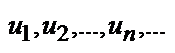+, члены таковы, что 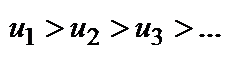и 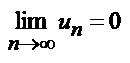, то ряд сходится, его сумма + и не > первого члена.

Функциональные ряды. Область сходимости.

Определение. Частными (частичными) суммами функционального ряда 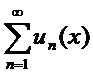называются функции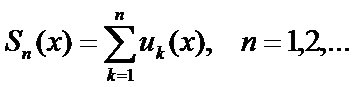

Определение. Функциональный ряд 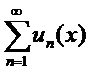называется сходящимся в точке (х=х₀), если в этой точке сходится последовательность его частных сумм. Предел последовательности 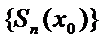называется суммойряда 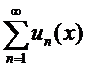в точке х₀.

Определение. Совокупность всех значений х, для которых сходится ряд 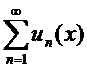называется областью сходимостиряда.

Определение. Ряд 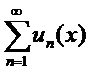называется равномерно сходящимся на отрезке [a,b], если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.

Разложение в ряд Фурье функции в интервале (-l;l)

Ряд Фурье для функции f(x) периода Т = 2l, непрерывной или имеющей конечное число точек разрыва первого рода на отрезке [-l, l] имеет вид:

Приложение двойного интеграла

.

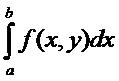Тройной интеграл

Пусть ограниченное множество {E_i}ÌR³. В трехмерном случае будем рассматривать области, имеющие в качестве своей границы кусочно-гладкие поверхности, т.е. области, имеющие кусочно-гладкие границы.

Определение: Поверхность называется глад­кой, если в любой его точке к ней можно про­вести касательную плоскость, непрерывно меняющуюся вместе с этой точкой. Поверхность называется кусочно-гладкой, если ее можно разрезать на конечное число гладких кусков.

Для трехмерных ограниченных плоскостей с кусочно-гладкими границами можно определить их объем (их трехмерную меру):

mЕ, mesE, DV.

Зададим на ЕÌR³ ограниченную функцию f. Зададим разбиение {E_i} и выберем точку х_i из {E_i}. Тогда интегральная сумма имеет вид:

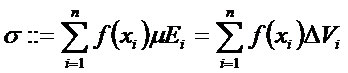
Если интегральная сумма имеет предел I при стремлении d{E_i}®0, то это число называется тройным интегралом от функции f на Е и обозна­чается:

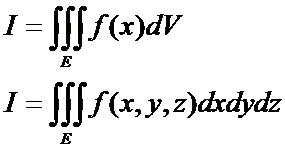
Приложение тройного интеграла.

Формула Грина.

Формула Остроградского – Грина устанавливает связь между криволинейным интегралом и двойным интегралом, т.е. дает выражение интеграла по замкнутому контуру через двойной интеграл по области, ограниченной этим контуром.

Будем считать, что рассматриваемая область односвязная, т.е. в ней нет исключенных участков.

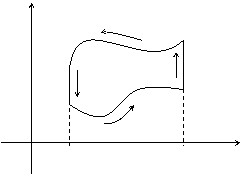y

y = y₂(x)

D

A

C

B

y= y₁(x)

0 x₁ x₂ x

Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде: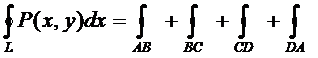

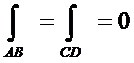
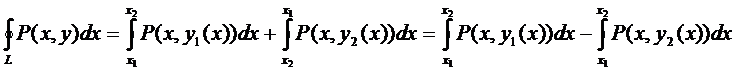
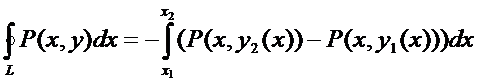
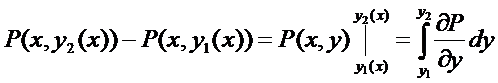
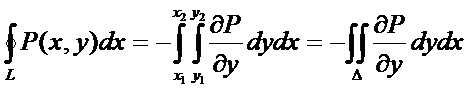
Если участки АВ и CD контура принять за произвольные кривые, то, проведя аналогичные преобразования

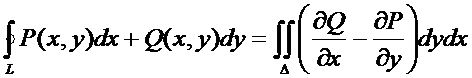
Формула Остроградского.

Рассматривается сначала поверхность, ограниченная сверху и снизу некоторыми поверхностями, заданными известными уравнениями, а сбоку ограниченную цилиндрической поверхностью. Затем рассматривается вариант когда поверхность ограничена цилиндрической поверхностью с образующими, параллельными дум доугим координатным осям

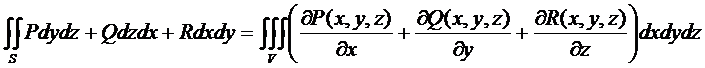
Отметим, что эта формула применима для вычисления поверхностных интегралов по замкнутой поверхности.

На практике формулу Остроградского можно применять для вычисления объема тел, если известна поверхность, ограничивающая это тело.

место формулы: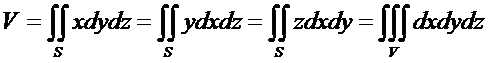

Пример. Найти формулу вычисления объема шара.

В поперечных сечениях шара (сечения параллельны плоскости XOY) получаются окружности.

Уравнение шара имеет вид: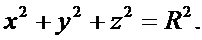

Найти объем шара можно по формуле:

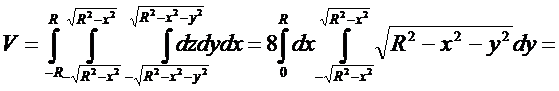
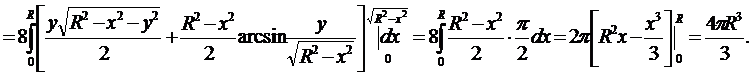Для решения этой же задачи можно воспользоваться преобразованием интеграла к сферическим координатам.

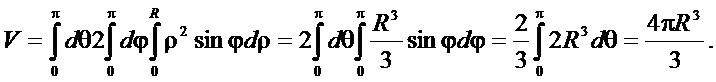
Векторные линии.

Дивергенция.

Определение. Выражение 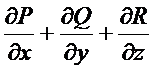называется дивергенцией вектора (дивергенцией векторной функции) 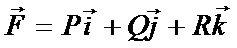и обозначается

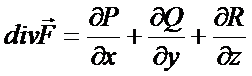
Таким образом, формулу Гаусса – Остроградского может быть записана в виде:

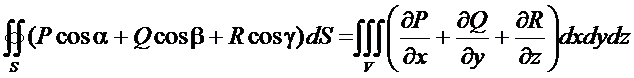
или

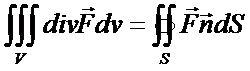
т.е. интеграл от дивергенции векторного поля 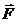по объему равен потоку вектора через поверхность, ограниченную этим объемом.

Ротор.

Определение. Вектор 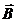, компоненты которого равны соответственно равны

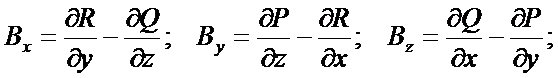
называется вихремили ротором вектора 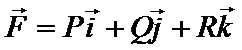и обозначается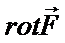

Формула Стокса.

Формула Стокса связывает криволинейные интегралы второго рода с поверхностными интегралами второго рода.

Пусть в пространстве задана некоторая поверхность S. L – непрерывный кусочно – гладкий контур поверхности S.

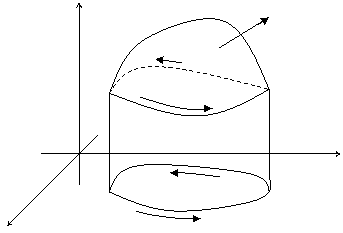
z S

L

y

D

l

x

Предположим, что функции P,Q и R непрерывны на поверхности S вместе со своими частными производными первого порядка. Применим формулу, выражающую криволинейный интеграл через определенный.

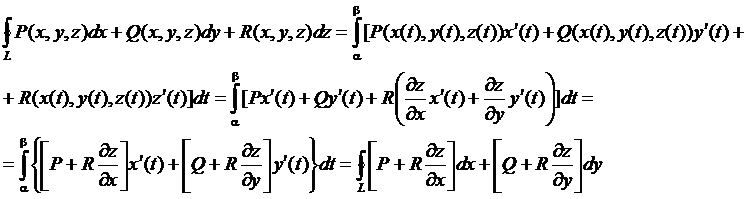
Введем обозначения: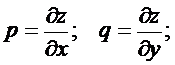

Применив формулу Грина, можно заменить криволинейный интеграл равным ему двойным интегралом. После преобразований устанавливается следуюшее соответствие между криволинейным и поверхностным интегралом:

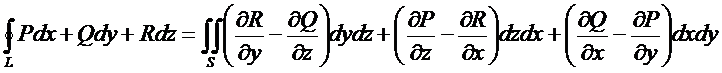
Циркуляция.

Определение. Криволинейный интеграл, представляющий собой работу векторного поля вдоль некоторой кривой L называется линейным интеграломот вектора 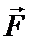по ориентированной кривой L.

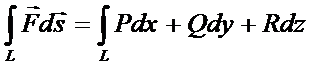
Если кривая L представляет собой замкнутый контур, то линейный интеграл по такому контуру называется циркуляцией вектроного поля 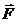вдоль контура L.

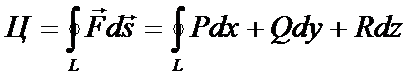
В векторной форме теорему Стокса можно сформулировать так:

Циркуляция вектора вдоль контура некоторой поверхности равна потоку вихря (ротора) через эту поверхность.

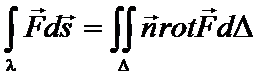
Отметим, что рассмотренная выше формула Грина – Остроградского является частным случаем формулы Стокса.

Также при условии равенства нулю всех компонент ротора вектора, получаем, что криволинейный интеграл по любой пространственной кривой равен нулю, т.е. криволинейный интеграл не зависит от пути интегрирования.

Потенциальное поле.

Если на области D существует функция f(x, y, z), имеющая непрерывные частные производные, для которых выполняются свойства: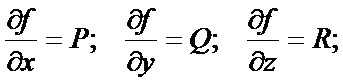

то такую функцию называют потенциальной функцией или потенциаломвектора .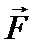

Тогда вектор 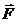является градиентом функции f.

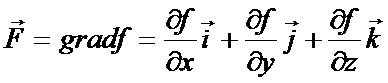
Потенциал может быть найден по формуле:

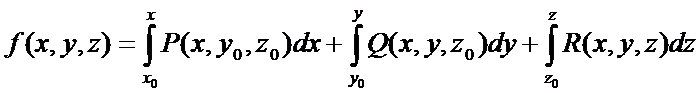
В этой формуле x₀, y₀, z₀ – координаты некоторой начальной точки. В качестве такой точки удобно брать начало координат.

Теорема.:

1) Интеграл от вектора 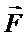по любому кусочно – гладкому контуру, принадлежащему области, равен нулю.

2) Интеграл по любому кусочно – гладкому пути, соединяющему две любые точки поля не зависит, от пути интегрирования.

Векторное поле 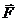называется соленоидальным (трубчатым), если div 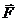=0 .

C помощью описанного выше оператора Гамильтона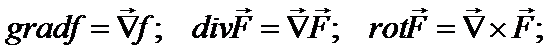

операторо Лапласа.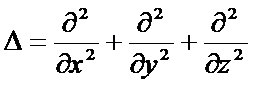

Справедливы следующие соотношения: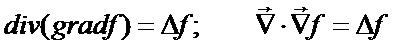

Уравнение таплопроводности.

Уравнение колебания струны.

Предельный признак сравнения.

Пусть имеем два ряда с положительными членами

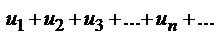(1) и 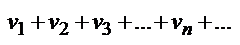(2), для которых выполняется условие: 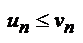. Тогда из сходимости ряда 2 следует сходимость ряда 1;

из расходимости ряда 1 следует расходимость ряда 2.

Предельный признак сравнения.

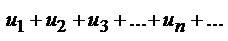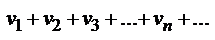Имеем два ряда (1) и (2).

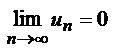. Если L существует, то оба ряда сходятся одновременно.

Пусть ряд 2 сходится, тогда по обычному признаку сравнения сходится и ряд 1.

Имеем ряд :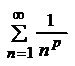

1) 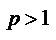ряд сходится

2) 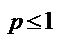ряд расходится.

Признак Даламера

Если в ряду с положительными членами 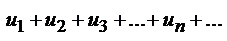отношение (n + 1)-го члена к n-му при имеет конечный предел l, то есть 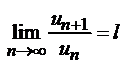, то

ряд сходится в случае ;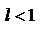

ряд расходится в случае ;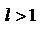

3) в случае 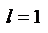ответа о сходимости или расходимости ряда теорема не дает.

Обобщеный признак Коши.

Если для ряда с положительными членами 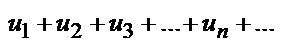величина 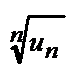имеет конечный предел l при 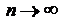, то есть 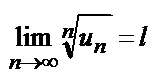, то

в случае 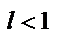ряд сходится;

в случае 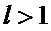ряд расходится;

3) в случае 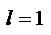ответа о сходимости или расходимости ряда теорема не дает.

Интегральный признак Коши.

Пусть члены ряда положительны и не возрастают, то есть 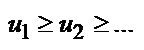и пусть f(х) – такая непрерывная не возрастающая функция, что , , .

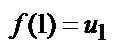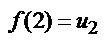Тогда справедливы следующие утверждения:

если несобственный интеграл 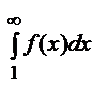сходится, то сходится и исходный ряд;

если указанный интеграл расходится, то расходится и исходный ряд.