Геометрический смысл определённого интеграла

Геометрический смысл определённого интеграла

Из истории математики известно, что одной из первых задач, приведшей к понятию определенного интеграла, является задача о вычислении площади криволинейной трапеции.

Определение:

Простейшей криволинейной трапецией будем называть фигуру, ограниченную

сверху – кривой y=f(x)

снизу – осью абсцисс y=0

слева – прямой x=a

справа – прямой x=b (см. рис. 1)

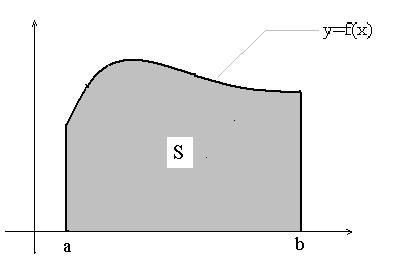
Рис. 1

1. Весь отрезок [a, b] разобьем на п частичных промежутков [x_i, х_i+1] длиной ∆x_i = x_i – х_i-1 , (i=1, 2, … , n), х₀ = a, x_п = b.

2. В каждом частичном промежутке произвольно выберем точку

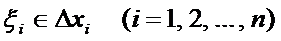
3. Составим интегральную сумму

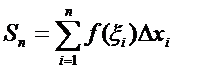
Очевидно, геометрически эта формула выражает площадь ступенчатой фигуры, составленной из прямоугольников (см. ниже рис. 2)

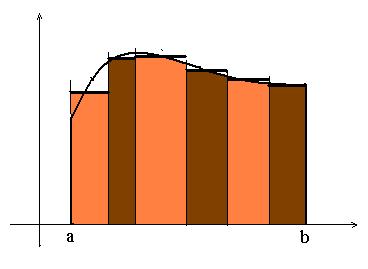
Рис. 2

4. Перейдем к пределу при п → ∞ при условии, что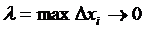

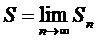(3)

При достаточно общих предположениях площадь ступенчатой фигуры стремится к площади криволинейной трапеции

Определение

Если существует конечный предел (3), то он называется определённым интегралом от функции f(х) по промежутку [a, b] и обозначается

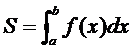
Числа а и b называются, соответственно, нижним и верхним пределами интегрирования, а функция f(x) – интегрируемой.

Отметим, что построенный по схеме 1) – 4) интеграл называется интегралом Римана. Однако, при менее жестких ограничениях на подинтегральную функцию такой интеграл может не существовать. Тем не менее, потребности прежде всего современной физики привели к созданию интеграла Лебега, обслуживающего более широкий класс функций. В математике используются и другие конструкции интеграла

Механический смысл определённого интеграла

Если известна скорость v(t) некоторого объекта в зависимости от времени t, то с помощью интегрирования можно легко определить пройденный этим объектом путь s(t), а именно,

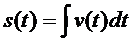
По аналогии, если известно ускорение a(t) некоторого объекта в зависимости от времени t, то с помощью интегрирования можно легко определить скорость движения этого объекта, а именно,

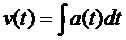
Предположим, что тело движется равноускоренно с ускорением а на временном периоде (0, t), причем в начальный момент времени скорость и путь равны нулю, т.е. a(t)=v^’(t)=a, v(0)=0, s(0)=0. Тогда

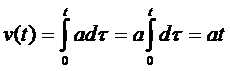
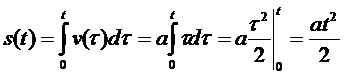
Итак, справедливы известные из школьного курса физики формулы

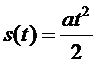
Ниже на графике ускорения (рис. 3) скорость тела численно равна площади заштрихованного прямоугольника

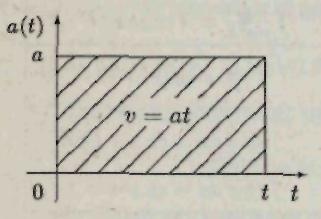
Рис. 3

Ниже на графике скорости (рис. 4) путь, пройденный телом за время (0, t), численно равен площади заштрихованного треугольника

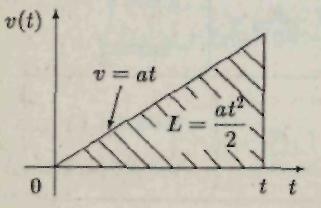
Рис. 4

Теорема Ньютона-Лейбница

Пусть функция f (х) определена, непрерывна и интегрируема на отрезке [a, b].

Определение

Интегралом с переменным верхним пределом называется интеграл следующего вида:

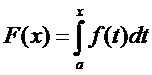
Здесь х – переменный верхний предел (a<x<b), t – переменная интегрирования (a<t<x). Геометрически интеграл с переменным верхним пределом означает площадь простейшей криволинейной трапеции, ограниченной справа прямой t=x. (см. рис. 5)

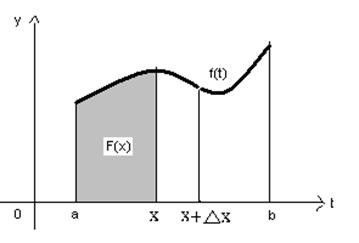
Рис. 5

Имеет место утверждение

Производная от интеграла с переменным верхним пределом равна подинтегральной функции

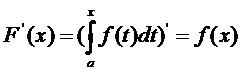(4)

Доказательство. Рассмотрим приращение 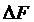функции F(x) в точке х:

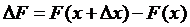
По определению имеем

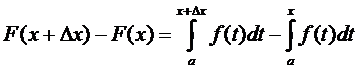(5)

Из рисунка 5 видно, что правую часть равенства (5) можно интерпретировать так: из трапеции aAD(x+ 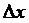)вычитается трапеция aACx. Ясно, что после вычитания остается узкая криволинейная трапеция xCD(x+ 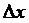) с основанием 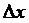. Ее площадь выражается интегралом

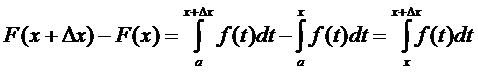(6)

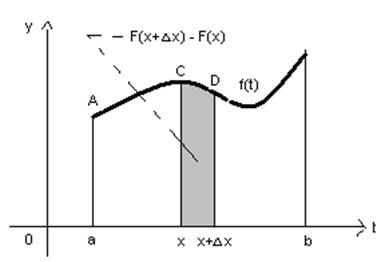
Рис. 6

По предположению функция y=f(x) непрерывна на промежутке [a, b]. Это позволяет считать, что площадь узкой криволинейной трапеции (на рис. 6 – закрашенная область) приблизительно равна площади прямоугольника с таким же основанием 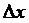и высотой f(с), где 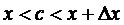. (см. рис. 7)

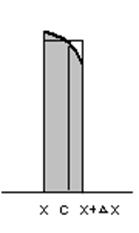
Рис. 6

Таким образом, равенство (6) можно заменить приближенным равенством

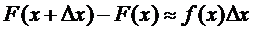
или

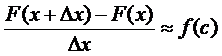
Переходя к пределу при 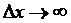, получаем

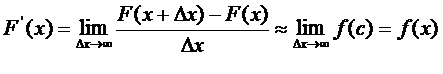
что и требовалось доказать

Формула Ньютона-Лейбница

Пусть функция f (х) определена, непрерывна и интегрируема на отрезке [a, b]. Тогда определённый интеграл находится по формуле:

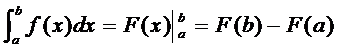
Действительно,

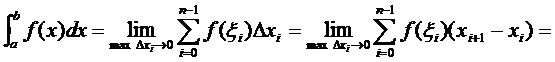
{согласно теореме Лагранжа о дифференцируемой функции}

=

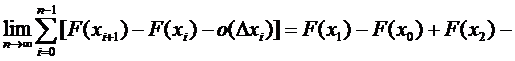
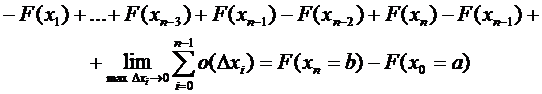
В определённом интеграле

Рассмотрим два простейших приема определенного интегрирования. Пусть функция f (x) имеет первообразную F (x). Покажем, что интеграл с переменным верхним пределом 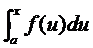также является первообразной функцией относительно f (x).

Вычислим производную от интеграла с переменным верхним пределом:

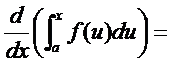
{воспользуемся формулой Ньютона-Лейбница}

=

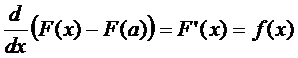
Далее 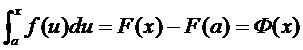- первообразная f (x)

Верно ли тождество

?

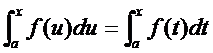Да, верно. В самом деле, переобозначение переменной интегрирования — это не замена переменной интегрирования.

Не всякий определённый интеграл с переменным верхним пределом может быть выражен в виде комбинации элементарных функций. В качестве примера таких интегралов, которые получили название специальных функций, приведём

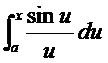— интегральный синус

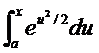— интеграл вероятностей

Теорема о среднем

Пусть функция f (x) непрерывна на отрезке [a, b]. Тогда найдется такая точка ξ 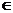(a, b), что выполняется равенство

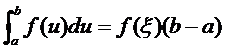, где ξ 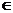(a, b)

Для обоснования этого равенства будем исходить из формулы Ньютона-Лейбница

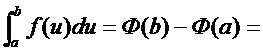
{по теореме Лагранжа} =

=

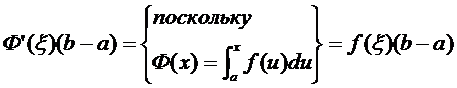
Каков геометрический смысл теоремы о среднем?

Всегда можно подобрать такую высоту прямоугольника, чтобы его площадь равнялась площади криволинейной трапеции с тем же основанием.

Оценка интеграла

m (b – a) < 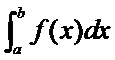< М (b – a), где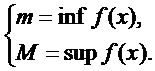

Это двойное неравенство является очевидным следствием теоремы о среднем

Пусть f [u (x)] непрерывна, а функция u (х) дифференцируема на [а, b], причём u (а) = с, u (b) = d. Тогда

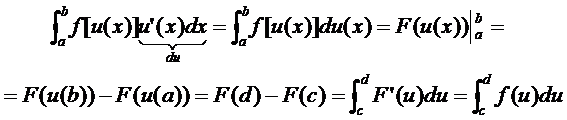
Заметим, что пределы интегрирования изменяются. Итак, формула замены переменной в определенном интеграле такова:

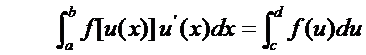
Пример 1. Вычислить .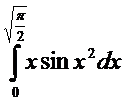

Решение.

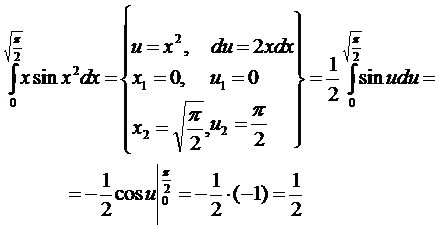
Выполним перенос производной под знаком интеграла 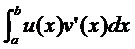, если функции u (х) и v (x) дифференцируемы на отрезке [a, b]. Для этого используем формулу дифференцирования произведения функций

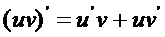или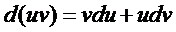

Теперь проинтегрируем это равенство

= 1 <

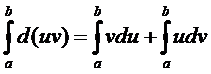
и окончательно получим:

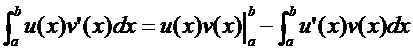
Итак, формула интегрирования по частям в сокращенной записи такова:

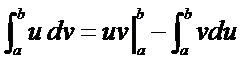
Пример 2. Вычислить интеграл .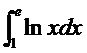

Решение.

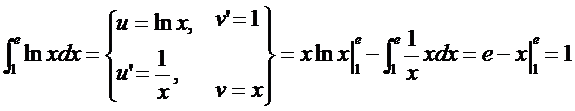
Решение.

Найдем объём тела вращения, если он ограничен плоскостями х = а, х = b и поверхностью, образованной вращением кривой у = f (x).

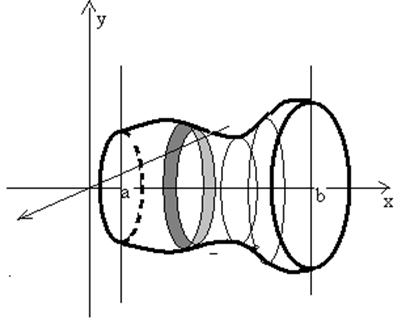
В качестве элемента интегральной суммы примем объём диска:

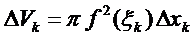
Переходя к пределу при , получаем следующую формулу вычисления объема тела вращения:

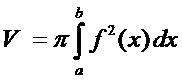
Пример 2. Найти объем шара радиуса R.

Решение.Вращением какой кривой описывается шар? Ответ: Вращением полуокружности. Уравнение верхней центральной полуокружности радиуса R: 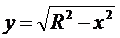Отсюда получаем

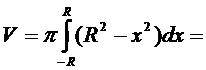
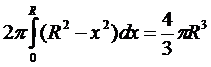
Несобственные интегралы

До сих пор мы занимались вычислением интегралов на ограниченном промежутке от ограниченной функции. В некоторых случаях эти ограничения на область и на функцию можно снять.Однако, прежде чем вычислять, такие интегралы необходимо сначала исследовать на сходимость.

Интеграл называется несобственным интегралом 1 рода,если его область интегрирования неограниченна, т.е. один из пределов или оба сразу принимают бесконечные значения

Интеграл называется несобственным интегралом 2 рода, если его подынтегральная функция неограниченна, т.е. минимум или (и) максимум функции в некоторой точке промежутка интегрирования принимают бесконечные значения

Говорят, что несобственный интеграл сходится, если существует предел этого интеграла в точке разрыва подынтегральной функции или в бесконечно удалённой точке. В противном случае говорят, что несобственный интеграл расходится

Решение.

.

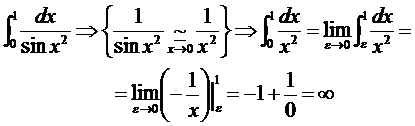Ответ: Заданный интеграл расходится

Формула прямоугольников

Формула трапеций

Геометрический смысл определённого интеграла

Из истории математики известно, что одной из первых задач, приведшей к понятию определенного интеграла, является задача о вычислении площади криволинейной трапеции.

Определение:

Простейшей криволинейной трапецией будем называть фигуру, ограниченную

сверху – кривой y=f(x)

снизу – осью абсцисс y=0

слева – прямой x=a

справа – прямой x=b (см. рис. 1)

Рис. 1

1. Весь отрезок [a, b] разобьем на п частичных промежутков [x_i, х_i+1] длиной ∆x_i = x_i – х_i-1 , (i=1, 2, … , n), х₀ = a, x_п = b.

2. В каждом частичном промежутке произвольно выберем точку

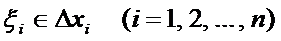
3. Составим интегральную сумму

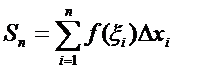
Очевидно, геометрически эта формула выражает площадь ступенчатой фигуры, составленной из прямоугольников (см. ниже рис. 2)

Рис. 2

4. Перейдем к пределу при п → ∞ при условии, что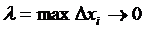

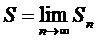(3)

При достаточно общих предположениях площадь ступенчатой фигуры стремится к площади криволинейной трапеции

Определение

Если существует конечный предел (3), то он называется определённым интегралом от функции f(х) по промежутку [a, b] и обозначается

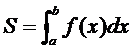
Числа а и b называются, соответственно, нижним и верхним пределами интегрирования, а функция f(x) – интегрируемой.

Отметим, что построенный по схеме 1) – 4) интеграл называется интегралом Римана. Однако, при менее жестких ограничениях на подинтегральную функцию такой интеграл может не существовать. Тем не менее, потребности прежде всего современной физики привели к созданию интеграла Лебега, обслуживающего более широкий класс функций. В математике используются и другие конструкции интеграла