Определение первообразной и неопределенного интеграла их свойства
Определение первообразной и неопределенного интеграла их свойства
Определение первообразной.
Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство 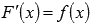 для любого х из заданного промежутка.
для любого х из заданного промежутка.
Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство 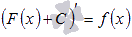 . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
Метод интегрирования подстановкой
Интегрирование методом подстановки.
Суть метода заключается в том, что мы вводим новую переменную, выражаем подынтегральную функцию через эту переменную, в результате приходим к табличному (или более простому) виду интеграла.
Очень часто метод подстановки выручает при интегрировании тригонометрических функций и функций с радикалами.
Пример.
Найти неопределенный интеграл 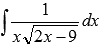 .
.
Решение.
Введем новую переменную 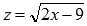 . Выразим х через z:
. Выразим х через z:
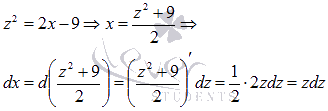
Выполняем подстановку полученных выражений в исходный интеграл:
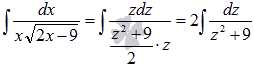
Из таблицы первообразных имеем 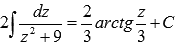 .
.
Осталось вернуться к исходной переменной х:
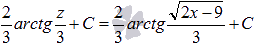
Ответ:
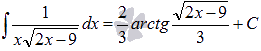
При интегрировании функций с иррациональностью вида 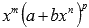 , где m, n, p – рациональные числа, важно правильно выбрать выражение для введения новой переменной. Смотрите рекомендации в разделе интегрирование иррациональных функций.
, где m, n, p – рациональные числа, важно правильно выбрать выражение для введения новой переменной. Смотрите рекомендации в разделе интегрирование иррациональных функций.
Очень часто метод подстановки используется при интегрировании тригонометрических функций. К примеру, использование универсальной тригонометрической подстановки позволяет преобразовать подынтегральное выражение к дробно рациональному виду.
Метод подстановки позволяет объяснить правило интегрирования 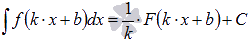 .
.
Вводим новую переменную 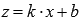 , тогда
, тогда
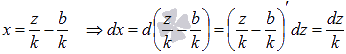
Подставляем полученные выражения в исходный интеграл:
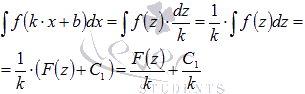
Если принять 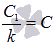 и вернуться к исходной переменной х, то получим
и вернуться к исходной переменной х, то получим
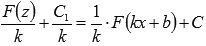
По частям
Интегрирование по частям.
Интегрирование по частям основано на представлении подынтегрального выражения в виде произведения 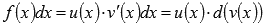 и последующем применении формулы
и последующем применении формулы 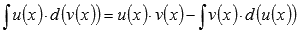 . Этот метод является очень мощным инструментом интегрирования. В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата. Для примера найдем множество первообразных функции арктангенс.
. Этот метод является очень мощным инструментом интегрирования. В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата. Для примера найдем множество первообразных функции арктангенс.
Пример.
Вычислить неопределенный интеграл 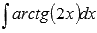 .
.
Решение.
Пусть 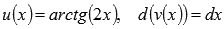 , тогда
, тогда
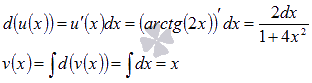
Следует отметить, что при нахождении функции v(x) не прибавляют произвольную постоянную С.
Теперь применяем формулу интегрирования по частям:
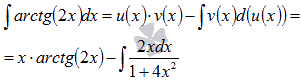
Последний интеграл вычислим по методу подведения под знак дифференциала.
Так как 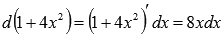 , то
, то 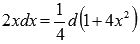 . Поэтому
. Поэтому 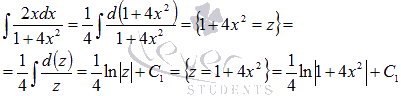
Следовательно,
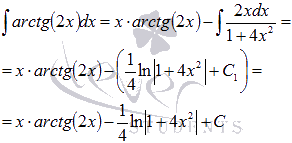
где 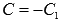 .
.
Ответ:
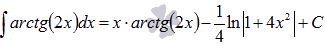 .
.
Основные трудности при интегрировании по частям порождает выбор: какую часть подынтегрального выражения брать за функцию u(x), а какую за дифференциалd(v(x)).
5,6 интегрирование правильных и неправильных рац дробей
Для интегрирования рациональной функции P(x)Q(x), где P(x) и Q(x) − полиномы, используется следующая последовательность шагов:
Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;
Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;
Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;
Вычислить интегралы от простейших дробей.
Рассмотрим указанные шаги более подробно.
Шаг 1. Преобразование неправильной рациональной дроби
Если дробь неправильная (т.е. степень числителя P(x) больше степени знаменателя Q(x)), разделим многочлен P(x) на Q(x). Получим следующее выражение:
P(x)Q(x)=F(x)+R(x)Q(x),
где R(x)Q(x) − правильная рациональная дробь.
Три подстановки Эйлера
Рассмотрим интегралы, подынтегральное выражение которых является рациональной функцией от переменной интегрирования и квадратного корня из квадратного многочлена.
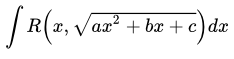 Такие интегралы могут быть сведены к интегралам от рациональных функций одной из трех подстановок Эйлера:
Такие интегралы могут быть сведены к интегралам от рациональных функций одной из трех подстановок Эйлера:

Выбор подстановки Эйлера
Как видно, для вычисления интеграла, можно применять не одну подстановку Эйлера. Все они приводят к интегралу от рациональной функции. Выбор в пользу той или иной подстановки следует делать, чтобы упростить вычисления.

Дифференциальный бином
Интегралы от дифференциального бинома сводятся к интегралам от рациональных функций в трех случаях, при определенных соотношениях между показателями степеней. Даны три подстановки, которые позволяют свести интеграл к интегралу от рациональной функции. Даны формулы приведения, которые позволяют свести интегралы к другим показателям степеней. Подробноразобранпримервычисленияинтегралаотдифференциальногобинома.


Определенный интеграл
Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где 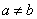 ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
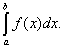
Как видно на графиках внизу (приращение первообразной функции обозначено 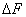 ),определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F(b) - F(a)).
),определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F(b) - F(a)).
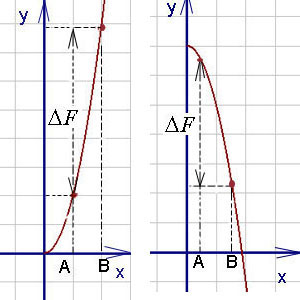
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,
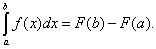 (38)
(38)
Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:
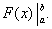
Поэтому формулу Ньютона-Лейбница будем записывать и так:
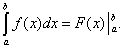 (39)
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому

Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.
Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b, далее - значение нижнего предела a и вычисляется разностьF(b) - F(a). Полученное число и будет определённым интегралом..
Несобственный интеграл
Что значит вычислить несобственный интеграл? Вычислить несобственный интеграл – это значит, найти ЧИСЛО(точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
ФНП
1.Основные понятия.
Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.
Обычно функция нескольких переменных задается явным аналитическим способом. Например: z=3x+5y2,u=xy+z2 и т.д.
Встречается также и неявное задание таких функций, например: z-2x-sinxy=0.
Упорядоченная пара чисел (x,y) может рассматриваться как точка на плоскости, т.е. Z есть функция точки (x,y).
Чтобы задать функцию z=f(x,y), надо не только указать правило нахождения z по заданным x и y, но и то множество (называемое областью задания функции) пар значений, которые могут принимать аргументы x и y.
Например, функция z= 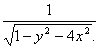 задана только при 1-y
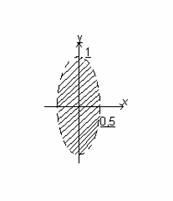
задана только при 1-y 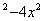 >0, т.е. внутри эллипса y2+4x2<1 с полуосями, а=0,5 и в=1 не включая точки, лежащие на эллипсе.
>0, т.е. внутри эллипса y2+4x2<1 с полуосями, а=0,5 и в=1 не включая точки, лежащие на эллипсе.


 Определение. Если каждой совокупности значений переменных x,y,z…t соответствует определенное значение переменной w, то w называется функцией независимых переменных x,y,z…t и записывается w=f(x,y,z…t).
Определение. Если каждой совокупности значений переменных x,y,z…t соответствует определенное значение переменной w, то w называется функцией независимых переменных x,y,z…t и записывается w=f(x,y,z…t).
Для функции трех переменных областью определения является упорядоченная тройка чисел (x,y,z), т.е. некоторая совокупность точек пространства. Область определения функции четырех и большего числа переменных не допускает простого геометрического истолкования. 
Функции двух переменных допускают графическую иллюстрацию. Графиком функции z=f(x,y), заданной на некотором множестве D точек плоскости ХОУ, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежит D, а z=f(x,y). В наиболее простых случаях такой график представляет собой некоторую поверхность.
Например, графиком функции z=4-x2-y2 является параболоид.
17 пространство Rnоткрытые, замкнутые связные
Определение 1. Упорядоченная совокупность из n действительных чисел 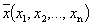 называется n-мерной точкой.
называется n-мерной точкой.
Определение 2. Расстоянием между двумя n-мерными точками 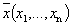
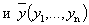 называется величина
называется величина
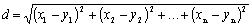 .
.
Определение 3. Совокупность всех n-мерных точек с введенной на ней метрикой 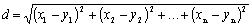 называется n-мерным евклидовым (метрическим) пространством Rn.
называется n-мерным евклидовым (метрическим) пространством Rn.
Пример 1. R2. M(a,b) - точка из R2, в линейном векторном
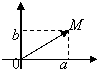 пространстве Е2 аналогично обозначается вектор
пространстве Е2 аналогично обозначается вектор 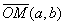 . Между точками и векторами с одинаковыми координатами существует взаимно однозначное соответствие. Поэтому в дальнейшем мы будем обозначать их одинаково:
. Между точками и векторами с одинаковыми координатами существует взаимно однозначное соответствие. Поэтому в дальнейшем мы будем обозначать их одинаково: 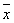 .
.
Пример 2.R1. 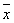 =а.
=а.



0 a
Определение 4. 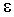 -окрестностью точки
-окрестностью точки 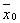 в Rn называется множество точек
в Rn называется множество точек 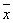 , удовлетворяющих условию
, удовлетворяющих условию 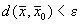 .
.
Пример 3.R2 R
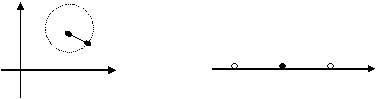
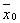
e
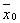 -e
-e 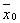
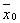 +e
+e
Определение 5. Множество А 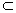 Rn называется открытым, если любая точка входит в него вместе с некоторой окрестностью.
Rn называется открытым, если любая точка входит в него вместе с некоторой окрестностью.
Определение 6.Множество B 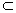 Rn называется замкнутым, если оно является дополнением до некоторого открытого множества.
Rn называется замкнутым, если оно является дополнением до некоторого открытого множества.
В - замкнутое ó Rn \ B - открытое.
Пример 4. R1.



-11
(-1,1) - открытое,
[-1,1] - замкнутое.
Открытые множества: (a,b), (-¥,a), (a,+¥), R, Æ.
Замкнутые множества: А=[a,b], R \ A, (-¥,a], [а,+¥) , R, Æ.
Пример 5. R2.
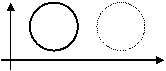 Без границ – открытое множество,
Без границ – открытое множество,
с границами - замкнутое.
Определение 7. Отрезком в Rn , соединяющим точки 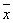 и
и 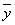 , называется множество точек, удовлетворяющее условию
, называется множество точек, удовлетворяющее условию 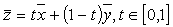 .
.
Определение 8. Множество А 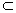 Rn называется выпуклым, если вместе с любыми двумя точками, входящими в него, оно содержит отрезок, их соединяющий.
Rn называется выпуклым, если вместе с любыми двумя точками, входящими в него, оно содержит отрезок, их соединяющий.

Выпуклые множества. Невыпуклые множества.
Определение 9. Точка х 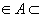 Rn называется угловой точкой множества А, если она не является внутренней ни для какого отрезка, целиком лежащего в А.
Rn называется угловой точкой множества А, если она не является внутренней ни для какого отрезка, целиком лежащего в А.
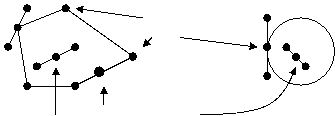 Угловые точки
Угловые точки
Неугловые точки
Теорема. Пересечение конечного числа выпуклых множеств есть выпуклое множество.
Доказательство. Пусть А и В - выпуклые множества.
Докажем, что 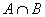 - выпуклое множество.
- выпуклое множество.
Пусть х, у 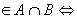
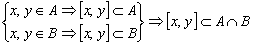 .
.
Следовательно, 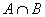 - выпуклое множество.
- выпуклое множество.
Предел и непрерывность ФНП
Непрерывность функции нескольких переменных.
Определение. Число А называется пределом функции f(M), где М(x1,x2,…xn) – точка n-мерного пространства, при стремлении точки М к точке М0(x10,x20,…xn0) любым образом, если для всякого сколь угодно малого 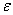 >0 существует такое число
>0 существует такое число 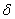 >0, что из условия
>0, что из условия 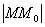 <
< 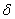 , где
, где 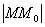 - расстояние между точками М и М0, следует
- расстояние между точками М и М0, следует 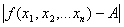 <
< 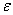 .
.
Обозначается:
А 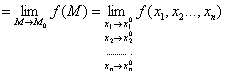 .
.
Пусть z=f(x,y). Придадим x и y приращения 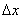 и
и 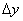 . Получим приращение
. Получим приращение 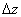 функции z=f(x,y). Если
функции z=f(x,y). Если
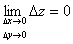 , (1)
, (1)
т.е. бесконечно малым аргументам соответствует бесконечно малое приращение функции, то говорят, что функция непрерывна.
Распишем 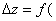 x0+
x0+ 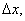 y+
y+ 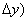 -f(x0,y0) и положим x0+
-f(x0,y0) и положим x0+  x=x,y0+
x=x,y0+ 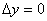 ,то выражение(1) можно записать в виде
,то выражение(1) можно записать в виде
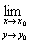 f(x,y)=f(x 0,y0), (2)
f(x,y)=f(x 0,y0), (2)
т.е. непрерывность функции означает, что ее предел равен ее значению от пределов аргументов.
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области. Если в некоторой точке не выполняется условие (2), то эта точка называется точкой разрыва.
Теорема 1.
В точке экстремума дифференцируемой функции все ее первые частные производные равны нулю,если 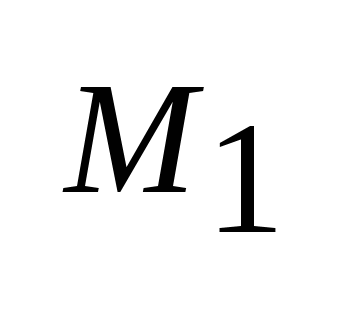 -экстремум ф-ции.
-экстремум ф-ции.
Теорема 2.
Пусть функция z=/(х,у) имеет непрерывные частные производные до второго порядка включительно в некоторой окрестности точки М0(а,b).
Если ее первые частные производные в точке М0 равны нулю, а вторые принимают значения
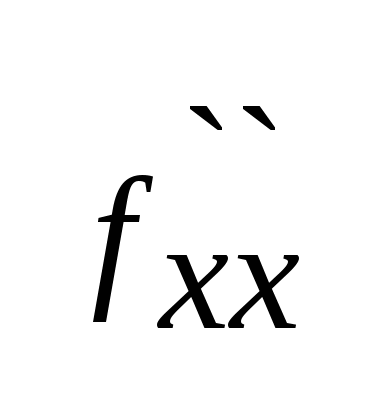 (a,b)=A,
(a,b)=A, 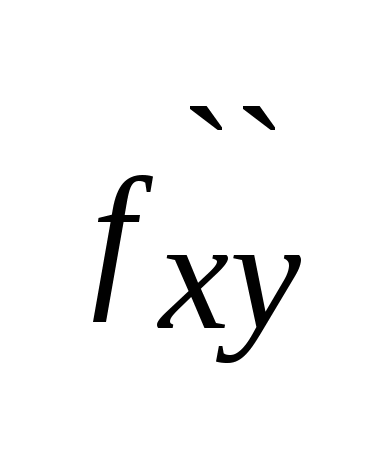 (a,b)=B,
(a,b)=B, 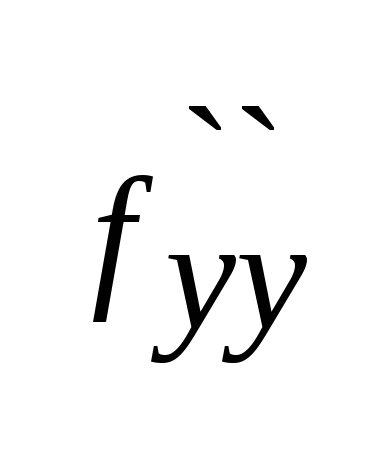 (a,b)=C,
(a,b)=C,
Топри
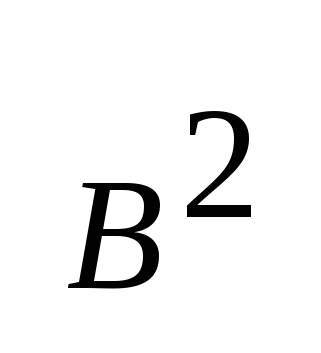 -АС<0 и А>0
-АС<0 и А>0
точка М0является точкой минимума данной функции, а при
В2-АС<0, А<0
точкой максимума, при
В2-АС>0
в точке М0экстремума нет.
Теорема (достаточное условие экстремума функции двух переменныx). Пусть функция z = f(x, y):
а) определена в некоторой окрестности критической точки (x0, y0), в которой f'x(x0, y0) = 0 и f'y(x0, y0) = 0;
б)имеет в этой точке непрерывные частные производные второго порядка f''xx(x0, y0) = A; f'xy(x0, y0) = f''yx(x0, y0) = B; f'yy(x0, y0) = C. Тогда, если Δ = AC - B2 > 0, то в точке (x0, y0) функция z = f(x, y) имеет экстремум, причём если A < 0 - максимум, если A > 0 -минимум. В случае Δ = AC - B2 < 0, функция z = f(x, y) экстремума не имеет. Если Δ = AC - B2 = 0, то вопрос о наличии экстремума остаётся открытым.
Тройной интеграл



Применение в геометрии
Если некоторое тело ограничено областью G трехмерного пространства, то объем данного тела будет равен
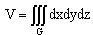
Применение в механике
Пусть в трехмерном пространстве находится тело, ограниченное областью G, причем плотность в каждой точке этого тела определяется формулой 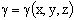 .
.
1. Масса тела: 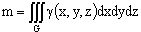
2. Статические моменты тела относительно плоскостей Oxy, Oxz, Oyz:
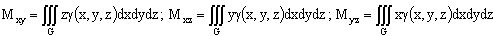
3. Координаты центра тяжести 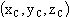 :
:
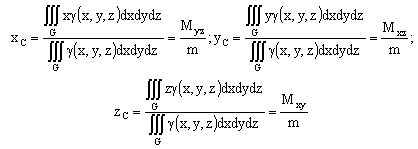
4. Моменты инерции тела относительно плоскостей Oxy, Oxz, Oyz и начала координат:
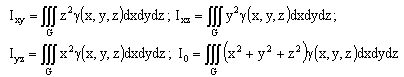
Определение первообразной и неопределенного интеграла их свойства
Определение первообразной.
Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство 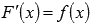 для любого х из заданного промежутка.
для любого х из заданного промежутка.
Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство 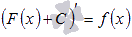 . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
