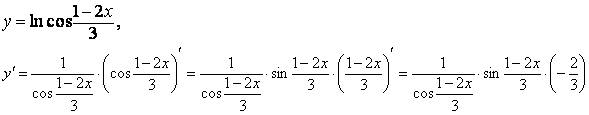Нахождение асимптот графика функции

Определение. Асимптотой графика функции 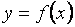называется прямая, обладающая тем свойством, что расстояние от точки 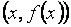графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

По способам их отыскания выделяют три вида асимптот: вертикальные 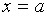, горизонтальные 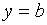, наклонные .

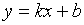Очевидно, горизонтальные являются частными случаями наклонных (при ).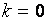

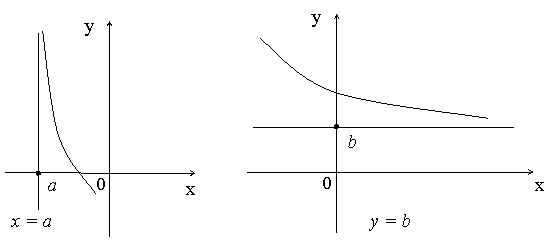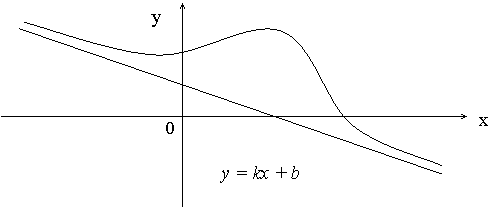Нахождение асимптот графика функции основано на следующих утверждениях.

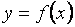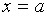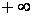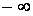Теорема 1. Пусть функция определена хотя бы в некоторойполуокрестности точки и хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равен или . Тогда прямая 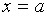является вертикальной асимптотой графика функции.

Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).

Теорема 2. Пусть функция 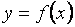определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции 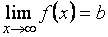. Тогда прямая 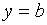есть горизонтальная асимптота графика функции .

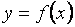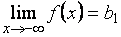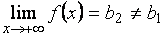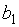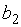Может случиться, что , а , причем и - конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов 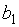или 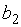, то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.

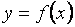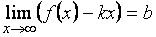Теорема 3. Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределы и . Тогда прямая 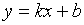является наклонной асимптотой графика функции .

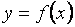Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.

Наклонная асимптота так же, как и горизонтальная, может быть односторонней.

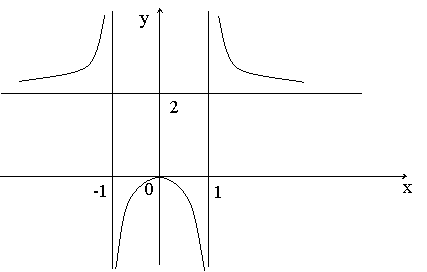
Пример. Найдите все асимптоты графика функции .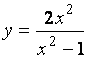

Решение.

Функция определена при 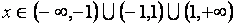. Найдем ее односторонние пределы в точках .

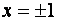Так как 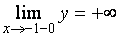и 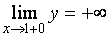(два других односторонних предела можно уже не находить), то прямые 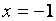и 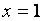являются вертикальными асимптотами графика функции.

Вычислим

(применим правило Лопиталя) =

.

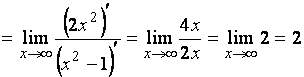Значит, прямая 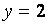- горизонтальная асимптота.

Так как горизонтальная асимптота существует, то наклонные уже не ищем (их нет).

33 1Функции нескольких переменных.

Основные понятия.

Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.

Обычно функция нескольких переменных задается явным аналитическим способом. Например: z=3x+5y²,u=xy+z² и т.д.

Встречается также и неявное задание таких функций, например: z-2x-sinxy=0.

Упорядоченная пара чисел (x,y) может рассматриваться как точка на плоскости, т.е. Z есть функция точки (x,y).

Чтобы задать функцию z=f(x,y), надо не только указать правило нахождения zпо заданным x и y, но и то множество (называемое областью задания функции) пар значений, которые могут принимать аргументы x и y.

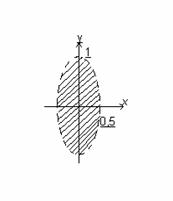
Например, функция z= 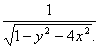задана только при 1-y 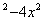>0, т.е. внутри эллипса y²+4x²<1 с полуосями, а=0,5 и в=1 не включая точки, лежащие на эллипсе.

Определение. Если каждой совокупности значений переменныхx,y,z…t соответствует определенное значение переменной w, то w называется функцией независимых переменных x,y,z…t и записываетсяw=f(x,y,z…t).

Для функции трех переменных областью определения является упорядоченная тройка чисел (x,y,z), т.е. некоторая совокупность точек пространства. Область определения функции четырех и большего числа переменных не допускает простого геометрического истолкования.

Функции двух переменных допускают графическую иллюстрацию. Графиком функции z=f(x,y), заданной на некотором множестве D точек плоскости ХОУ, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежит D, а z=f(x,y). В наиболее простых случаях такой график представляет собой некоторую поверхность.

Например, графиком функции z=4-x²-y² является параболоид.

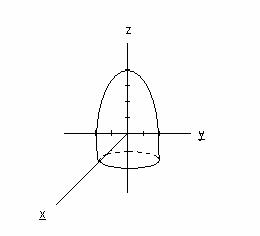
Функции трех и большего числа переменных не имеют геометрического представления.

2.Непрерывность функции нескольких переменных.

Определение. Число А называется пределом функции f(M), где М(x₁,x₂,…x_n)– точка n-мерного пространства, при стремлении точки М к точке М₀(x₁⁰,x₂⁰,…x_n⁰) любым образом, если для всякого сколь угодно малого 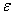>0 существует такое число 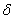>0, что из условия 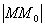< 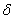, где 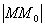- расстояние между точками М и М₀, следует < .

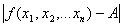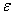Обозначается:

А .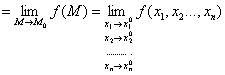

Пусть z=f(x,y). Придадим x и y приращения 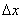и 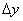. Получим приращение 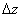функции z=f(x,y). Если

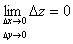, (1)

т.е. бесконечно малым аргументам соответствует бесконечно малое приращение функции, то говорят, что функция непрерывна.

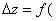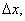Распишем x₀+ y+ 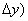-f(x₀,y₀) и положим x₀₊ x=x,y₀+ 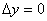,то выражение(1) можно записать в виде

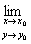f(x,y)=f(x ₀,y₀), (2)

т.е. непрерывность функции означает, что ее предел равен ее значению от пределов аргументов.

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области. Если в некоторой точке не выполняется условие (2), то эта точка называется точкой разрыва.

3 ПОВТОРНЫЙ ПРЕДЕЛ

- предел функции нескольких переменных, при к-ром предельный переход совершают последовательно по различным переменным. Пусть, напр., функция f двух переменных х и уопределена на множестве вида 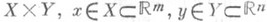, и пусть х ₀, y₀ - предельные точки соответственно множеств Xи Y или символы оо (в случае, когда m=1 или n=1, х ₀ и соответственно y₀ могут быть бесконечностями со знаком: 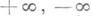). Если при любом фиксированном 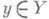существует предел

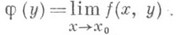(1) и у функции j(у).существует предел

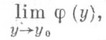
то этот предел наз. повторным пределом

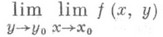(2)

функции f(x, у).в точке ( х ₀, у ₀). Аналогично определяется П. п.

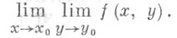(3)

Если существует (конечный или бесконечный) двойной предел

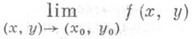(4)

и при любом фиксированном существует конечный предел (1), то существует и П. п. (2) и он равен двойному пределу (4).

Если при каждом 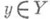существует предел (1), а при каждом 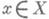существует предел

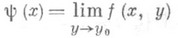
и если при 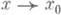функция f(x, у).стремится на Y к предельной функции j(у).равномерно относительно у, то оба П. п. (2) и (3) существуют и равны друг другу. Если множества XиYявляются множествами натуральных чисел, то функция f наз. в этом случае двойной последовательностью и значения аргументов пишут в виде индексов:

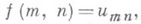
а П. п.

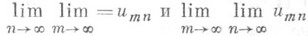
наз. повторным и пределами двойной последовательности. Понятие П. п. обобщается на случай, когда X, Y и множество значений функции f являются подмножествами нек-рыхтопологич. пространств.

4 ДВОЙНОЙ ПРЕДЕЛ

- 1) Д. п. последовательности, предел двойной последовательности {х _тп}, т, n=1, 2, ...,- число а, определяемое следующим образом: для любого е>0 существует такое N_e, что для всех m>N_e и n>N_eвыполняется неравенство

Обозначение: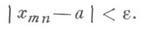

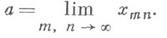
Если для любого e>0 существует такое N_e, что для всех m>N_e и n>N_e выполняется неравенство |x_mn|>e, то последовательность х _тп имеет своим пределом бесконечность: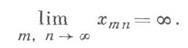

Аналогично определяются бесконечные пределы

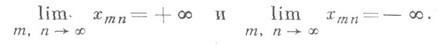
Д. п. последовательности является частным случаем Д. п. функции по множеству, а именно в случае, когда это множество состоит из точек плоскости с целочисленными координатами ти п. Поэтому между Д. п. последовательности и ее повторными пределами существует та же связь, что и в общем случае.

2) Д. п. функции - предел функции двух переменных, определяемый следующим образом. Пусть функция f(x, у)определена на множестве Е, расположенном в плоскостиXOY, а ( х ₀, у ₀)- его предельная точка. Число Аназ. Д. п. функции f(x, у )в точке ( х ₀, у ₀), или при 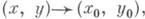если для любого e>0 существует такое d>0, что для всех точек 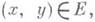координаты к-рых удовлетворяют неравенствам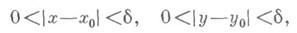

выполняется неравенство

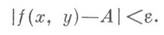
В этом случае пишут

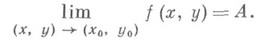
Используя понятие предела последовательности, определение Д. п. функции можно сформулировать следующим образом:

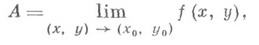
если для любой последовательности

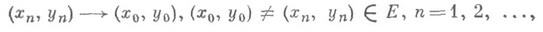
выполняется условие

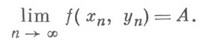
Аналогично формулируются определения Д. п. функции при стремлении аргумента к бесконечности, а также определения бесконечных Д. п. функции.

Существует связь между Д. п. функции и повторным пределом функции в точке (x₀, y₀) или в 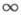: пусть х ₀ и у ₀- предельные точки (конечные или бесконечные) для числовых множеств Xи У, 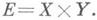Если суще-

ствуетконечный или бесконечный Д. п. функции

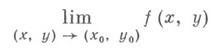
и при любом 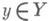существует конечный предел

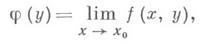
то существует и повторный предел

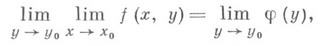
и он равен Д. п. функции.

Используя понятие окрестности, определению Д. п. функции можно придать следующий вид: пусть а- предельная точка (х ₀, у ₀ )множества Еили символ 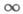, причем в последнем случае множество Енеограничено, А- число или один из символов 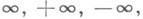тогда

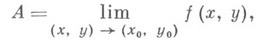
если для любой окрестности О _A точки или символа Асуществует такая окрестность О _а числа или символа а, что для всех выполняется условие В этом виде определение Д. п. функции переносится на случай, когда функция f определена на произведении топологич. пространств Xи Y, 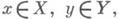а значения f(x, у )также принадлежат некоторому топологическиму пространству.

34Частные производные.

Частной производной функции нескольких переменных по какой-нибудь переменной в рассматриваемой точке называется обычная производная по этой переменной, считая другие переменные фиксированными (постоянными). Например, для функции двух переменных 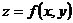в точке 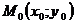частные производные определяются так:

,

,

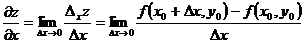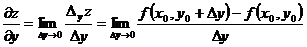если эти пределы существуют. Величина 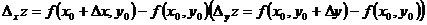называется частным приращением функции z в точке 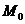по аргументу 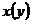. Используются и другие обозначения частных производных:

, , , ,

, , , .

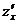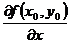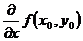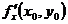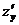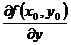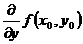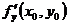Символы 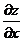, , 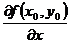, 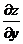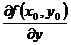как дроби трактовать нельзя (в этом отличие от случая одной переменной).

Из определения следует геометрический смысл частной производной функции двух переменных: частная производная 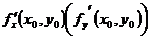- угловой коэффициент касательной к линии пересечения поверхности 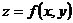и плоскости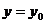 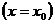в соответствующей точке.

Пользуясь понятием скорости изменения переменной, можно сказать, что частная производная 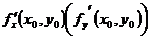есть скорость изменения функции 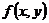относительно 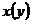при постоянном .

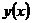Из определения частных производных следует, что правила вычисления их остаются теми же, что для функций одной переменной, и только требуется помнить, по какой переменной ищется производная.

Пример 1. Если 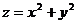, то , .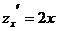

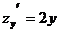Пример 2. Если 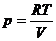, то 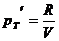, 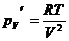. Величина 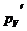называется изотермическим коэффициентом упругости идеального газа.

Аналогично определяются и обозначаются частные производные функции трех и большего числа независимых переменных.

ПОЛНОЕ ПРИРАЩЕНИЕ

функции нескольких переменных - приращение, приобретаемое функцией, когда все аргументы получают (вообще говоря, ненулевые) приращения. Точнее, пусть функция f определена в окрестности точки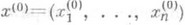

n-мерного пространства 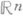переменных х ₁,. . ., х _п.Приращение

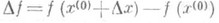
функции f в точке x⁽⁰⁾, где

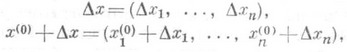
наз. полным приращением, если оно рассматривается как функция n всевозможных приращений Dx₁, . . ., Dx_nаргументов х ₁, . .., х _п, подчиненных только условию, что точка x⁽⁰⁾+Dx принадлежит области определения функции f. Наряду с П. п. функции рассматриваются частные приращения Dx_kf функции f в точке х ⁽⁰⁾ по переменной х _k, т. е. такие приращения Df, для к-рыхDx _уj=0, j=1, 2, . . ., k-1, k+1, . . ., п, k - фиксировано (k=1, 2, . . ., п).

35.

36.ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ

Пусть y = f(u), а u= u(x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.

Областью определения функции y = f(u(x)) является либо вся область определения функции u=u(x) либо та ее часть, в которой определяются значения u, не выходящие из области определения функции y= f(u).

Операция "функция от функции" может проводиться не один раз, а любое число раз.

Установим правило дифференцирования сложной функции.

Теорема. Если функция u= u(x) имеет в некоторой точке x₀ производную 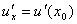и принимает в этой точке значение u₀ = u(x₀), а функция y= f(u) имеет в точке u₀ производную y '_u= f'(u₀), то сложная функция y = f(u(x)) в указанной точке x₀ тоже имеет производную, которая равна y '_x= f '(u₀)·u '(x₀), где вместо u должно быть подставлено выражение u= u(x).

Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x.

Доказательство. При фиксированном значении х₀ будем иметь u₀=u(x₀), у₀=f(u₀). Для нового значения аргумента x₀+Δx:

Δu= u(x₀ + Δx) – u(x₀), Δy=f(u₀+Δu) – f(u₀).

Т.к. u – дифференцируема в точке x₀, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. АналогичноприΔu→0 Δy→0.

По условию 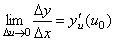. Из этого соотношения, пользуясь определением предела, получаем (при Δu→0)

,

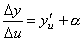где α→0 приΔu→0, а, следовательно, ипри Δx→0.

Перепишем это равенство в виде:

Δy= y '_uΔu+α·Δu.

Полученное равенство справедливо и при Δu=0 при произвольном α, так как оно превращается в тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены полученного равенства на Δx

.

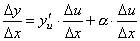По условию 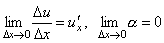. Поэтому, переходя к пределу при Δx→0, получим y '_x= y '_u·u '_x . Теорема доказана.

Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от "внешней" функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от "внутренней" функции по независимой переменной.

Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y '_x осуществляется последовательным применением предыдущей теоремы.

По доказанному правилу имеем y '_x= y '_u·u '_x . Применяя эту же теорему для u '_x получаем 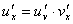, т.е.

y '_x = y '_x· u '_v· v '_x = f '_u (u)·u '_v (v)·v '_x (x).

Примеры.

1. y = sin x². Тогда .
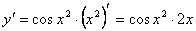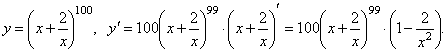
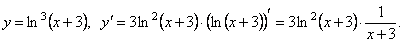
2. 
3. 
4.