Совершенное и несовершенное сжатие.

а) Сжатие струи называется совершенным, если стенки резервуара удалены от центра отверстия на расстояние l > 3dо и не оказывают влияния на сжатие струи.

б) Сжатие струи называется несовершенным, если стенки резервуара удалены от центра отверстия на расстояние l < 3dо и оказывают влияние на сжатие струи.

При совершенном сжатии струя сжата больше, чем при несовершенном сжатии.

Коэффициенты: ε, φ, μ, ζ , скорость и расход при совершенном сжатии определяются по формулам, приведенным выше для истечения из отверстия(9.1).

Скорость и расход при несовершенном сжатии

Боковые стенки успевают сформировать поток жидкости по направлению стенок при подходе к отверстию, струя сжимается в меньшей степени, чем при истечении из резервуара неограниченных размеров при совершенном сжатии. Увеличивается коэффициент сжатия и коэффициент расхода.

При несовершенном сжатии и больших числах Re, при известной скорости, диаметре и вязкости:

1. Коэффициент сжатия ε₁ определяется по эмпирической формуле

ε₁ = 0,62 +0,38/(S₀/S₁) (9.12)

где S₀/S₁ - отношение площади отверстия S₀ к площади S₁ поперечного сечения резервуара.

2. Коэффициент скорости φ по графику Альтшуля по числу Re.

3. Коэффициент расхода при несовершенном сжатии равен μ₁ = ε₁φ .

4. Коэффициент сопротивления отверстия при несовершенном сжатии по формуле

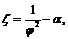где α = 1

Если скорость неизвестна, то φ, μ_1, ζнаходят из уравнения Бернулли, например, как на схеме рис.9.4

Уравнение Бернулли для сечений 1-1 и 2-2

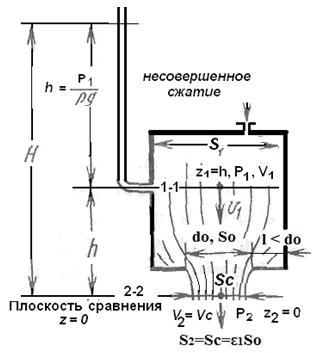
Рис.9.4. Истечение из отверстия при несовершенном сжатии в среду с давлением Р₂.

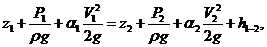
где 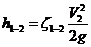- потеря напора между сечениями 1-1 и 2-2. За плоскость сравнения возьмем сечение 2.

V₂=Vс - скорость в сжатом сечении, S₂ = Sc = ε₁S₀.

Напор истечения равен: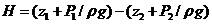

Выразим V₁ через V₂ :

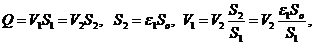обозначим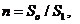

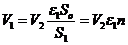
Подставим в уравнение Бернулли и получим зависимость напора истечения и скорости:

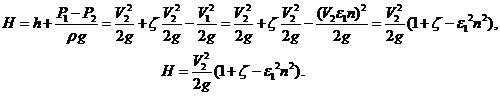
Cкорость в сжатом сечении струи при несовершенном сжатии

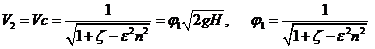(9.13)

Расход через отверстие при несовершенном сжатии струи и коэффициент расхода.

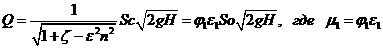(9.14)

Истечение под уровень

Истечением жидкости в резервуар, заполненный жидкостью, называется истечением под уровень (рис. 9.4). Кинетическая энергия струи теряется на вихреобразование.

Скорость и расход определяются из уравнения Бернулли для поверхности "1- 1" в резервуаре и сжатого сечения струи " 3– 3". За плоскость сравнения принимаем ось отверстия "3-3". 1-1 и 2-2 – уровни свободной поверхности в резервуарах.

Исходные данные по сечениям.

1-1: z₁= h₁, P₁ > Ратм, V₁ = 0, "3-3": z₃=0,Р₃, V₃=Vс.

Над свободной поверхностью 2-2 давление меньше атмосферного Р₂<Рат.

ξ ≈0,06 – коэффициент сопротивления отверстия принимаем таким же, как при истечении в атмосферу, α - коэффициент Кориолиса.

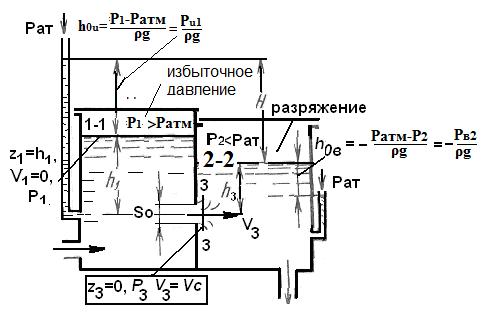
Рис.9.5. Истечение под уровень.

В левом баке над свободной поверхностью избыточное давление Р_и1= ρgh_0и.

В правом баке над свободной поверхностью вакуум Р_в2, давление на оси отверстия Р₃=Р_в2+ρgh₃

Уравнение Бернулли для сечений 1-1 и 3-3.

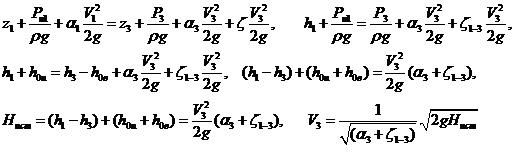
А надо бы выяснить: скоростной напор или потери при входе в резервуар!

Разность гидростатических напоров по обе стороны стенки равна напору истечения - Н_ист .

,

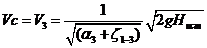
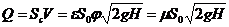где S_c – площадь сжатого сечения струи, S₀ – площадь отверстия, ζ_1-3=0,04-0,06- коэффициент потерь от сечения 1-1 до сечения 3-3, ε=0,6-0,62.