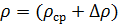Обработка результатов прямых многократных измерений

Пусть измеряется величина «а» (время, масса и т.д.).

Обозначим результат i-го измерения через 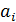(i=1,2,3…). Теория вероятности доказывает, что ближе всего к истинному значению лежит среднее арифметическое значение результатов измерений:

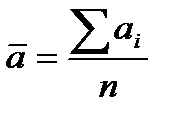
Абсолютная погрешность i-го измерения равна:

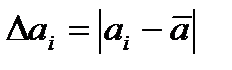
Показателем точности проведенных измерений считается среднеквадратичная погрешность результата n измерений:

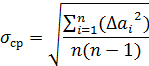
В прямых многократных измерениях результирующая погрешность определяется как погрешностями самой измеряемой величины, так и погрешностью измерительного прибора (инструментальной погрешностью). За инструментальную погрешность 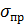обычно принимается точность прибора. Если точность прибора не указана, то за 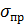принимается половина цены деления минимальной шкалы измерительного прибора.

В проводимых лабораторных работах с надежностью около 70% за доверительный интервал (абсолютную погрешность результатов измерений) принимается величина:

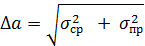
В этом случае результат измерений представляется в виде:

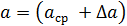
Значения 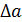берется с одной значащей цифрой, а величина 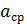округляется до соответствующего разряда в .

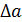Относительная погрешность измерений равна:

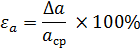
Обработка результатов косвенных измерений.

Пусть искомая величина является функцией нескольких непосредственно измеряемых величин:

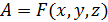
При прямых измерениях получено:

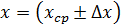
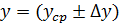
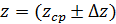
Среднее значение искомой величины находится через средние значения измеренных величин:

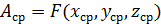
Метод прямого дифференцирования.

Находим полный дифференциал функции:

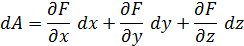
Частные производные в теории измерений называются коэффициентами влияния. Полагая dx, dy, dz , равными абсолютным погрешностям 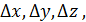и используя метод квадратичного суммирования, получаем формулу для определения абсолютной погрешности искомой величины:

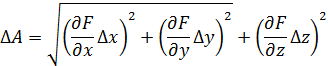
Относительная погрешность измерений равна:

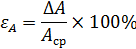
Метод логарифмического дифференцирования.

Применяется, когда функция F есть произведение измеряемых величин. В этом случае сначала находят натуральный логарифм от F, а затем проводят дифференцирование. Рассмотрим в качестве примера нахождение плотности тела цилиндрической формы. По определению

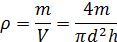
Находим среднее значение плотности тела

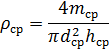
Логарифмируем функциональную зависимость

,

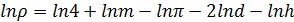а затем дифференцируем

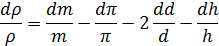
Заменяем дифференциалы на абсолютную погрешность и проводим квадратичное суммирование. Находим относительную погрешность измерений

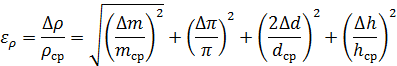
Погрешность табличных данных берется равной половине отброшенного разряда числа. Например, если π=3.14, то .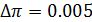

Абсолютная погрешность измерений равна:

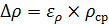
Результат измерений запишем в виде: