ФГАОУ ВПО «УрФУ имени первого Президента России Б.Н.Ельцина»
ФГАОУ ВПО «УрФУ имени первого Президента России Б.Н.Ельцина»
ТЕРМОДИНАМИКА. РАСТВОРЫ
Методические указания к лабораторным работам
По курсу «Физическая химия»
для студентов всех форм обучения металлургических специальностей
Екатеринбург
УДК 541.1
Составители: А.И. Михайлов, Н.Ю. Добрынина, Л.Н. Шибанова
Научный редактор: А.М. Панфилов
ТЕРМОДИНАМИКА. РАСТВОРЫ: Методические указания к лабораторным работам по курсу «Физическая химия» / А.И. Михайлов, Н.Ю. Добрынина, Л.Н. Шибанова. Екатеринбург: ФГАОУ ВПО «УрФУ имени первого Президента России Б.Н.Ельцина», 2010. 51 с.
Методические указания предназначены для организации самостоятельной работы студентов всех видов обучения металлургических специальностей при выполнении лабораторных работ по курсу «Физическая химия».
В работе изложены теория и методика выполнения шести лабораторных работ, предусмотренных учебными программами курса «Физическая химия» (разделы «Термодинамика», «Термодинамика растворов»): изучение равновесия реакций газификации углерода и диссоциации карбонатов на примере CaCO3, определение теплот растворения солей в воде и коэффициента распределения вещества между двумя несмешивающимися жидкостями, определение парциально-молярных объемов компонентов в бинарных растворах, изучение концентрационной зависимости температуры замерзания раствора. Приведены необходимые справочные данные, изложена методика оценки погрешности измерений.
Библиогр.: 5 назв. Рис. 13. Табл. 8. Прил. 3.
| Подготовлено кафедрой «Теория металлургических процессов» |
© ФГАОУ ВПО «УрФУ имени первого Президента России Б.Н.Ельцина», 2010
СОДЕРЖАНИЕ
| ВВЕДЕНИЕ | ||
| 1. ОСНОВНЫЕ ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К СТУДЕНТАМ В ЛАБОРАТОРИИ | ||
| 2. ПОСТРОЕНИЕ ГРАФИКОВ | ||
| 3. ОЦЕНКА ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ | ||
| 4. ТЕРМОДИНАМИКА | ||
| Работа № 1. | ИЗУЧЕНИЕ РАВНОВЕСИЯ РЕАКЦИИ ГАЗИФИКАЦИИ УГЛЕРОДА ЕГО ДИОКСИДОМ | |
| Работа № 2. | ИЗУЧЕНИЕ УПРУГОСТИ ДИССОЦИАЦИИ CaCO3 | |
| Работа № 3 | ОПРЕДЕЛЕНИЕ ТЕПЛОТЫ РАСТВОРЕНИЯ СОЛИ В ВОДЕ | |
| 5. РАСТВОРЫ | ||
| Работа № 4. | ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА РАСПРЕДЕЛЕНИЯ ВЕЩЕСТВА В ДВУХ НЕСМЕШИВАЮЩИХСЯ ЖИДКОСТЯХ | |
| Работа № 5. | ОПРЕДЕЛЕНИЕ ПАРЦИАЛЬНО-МОЛЯРНЫХ ОБЪЕМОВ КОМПОНЕНТОВ БИНАРНОГО РАСТВОРА | |
| Работа № 6. | ОПРЕДЕЛЕНИЕ КРИОСКОПИЧЕСКОЙ ПОСТОЯННОЙ ВОДЫ | |
| ПРИЛОЖЕНИЕ 1 | Термодинамические свойства некоторых веществ | |
| ПРИЛОЖЕНИЕ 2 | Расчет величины 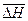 в работах №1 и №2 в работах №1 и №2 | |
| ПРИЛОЖЕНИЕ 3 | Интегральные теплоты растворения некоторых солей в воде при 25ºС | |
| Библиографический список |
ВВЕДЕНИЕ
Выполнение лабораторных работ по физической химии дает возможность более глубокого осмысления студентами соответствующих разделов теоретического курса, знакомит с некоторыми методами физико-химических исследований, закрепляет необходимые навыки самостоятельной обработки и анализа результатов наблюдений.
ОСНОВНЫЕ ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К СТУДЕНТАМ В ЛАБОРАТОРИИ
Техника безопасности
К выполнению лабораторных работ допускаются только лица, прошедшие вводный инструктаж по технике безопасности и имеющие соответствующую подпись в листке по учёту инструктажа.
Выводы следует излагать литературным языком, допуская лишь общепринятые сокращения. Полностью оформленный отчет о работе сдается на проверку преподавателю перед началом следующей работы или заранее в часы консультации.
ПОСТРОЕНИЕ ГРАФИКОВ
Графическое изображение опытных и расчетных данных облегчает сравнение величин, позволяет легко обнаружить характер изменения их (наличие максимумов, минимумов, точек перегиба и т.п.). В таблицах все эти особенности проявляются менее отчетливо.
При построении графиков необходимо соблюдать следующие основные правила:
2.1 Значение независимой переменной откладывают по оси абсцисс,
функции – по оси ординат.
2.2 Масштабы нужно выбирать так, чтобы координаты любой точки графика могли быть определены легко и быстро. Если расстояние между главными соседними линиями разделено на десять равных частей, то наиболее удобно выбирать такой масштаб, в котором это расстояние принято за одну, две, четыре или пять единиц. Цифровые обозначения этих величин необходимо проставлять равномерно вдоль всей оси. На каждой координатной оси необходимо проставить название представляемой ею величины и единицы, в которых она измеряется.
При выборе шкалы по осям координат нет необходимости откладывать величины с нулевого значения, если это не вызвано специальными соображениями (экстраполяция и т.п.). В соответствии с этим правилом шкала для каждой переменной величины может начинаться с наименьшего округленного значения из совокупности данных и заканчиваться округленным в сторону большего значения.
2.3 Масштаб желательно выбирать так, чтобы кривая проходила через всё поле графика, насколько это возможно.
2.4 Кривая должна быть плавной, проходить насколько возможно близко ко всем
нанесенным точкам. Примерно одна половина всех точек должна лежать по одну сторону кривой, а вторая – по другую. Кривая не должна содержать необъяснимых разрывов, самопересечений или других подобных особенностей.
Рекомендуется на графике четко выделять опытные точки, а кривую, проведенную по ним, представлять сравнительно тонкой линией. На линиях, полученных в результате теоретических расчетов, точки не проставляются.
ТЕРМОДИНАМИКА
Теоретическая часть
Равновесная система, состоящая из твердого углерода и смеси газов СО-СО2, обладает двумя степенями свободы, что следует из правила фаз Гиббса:
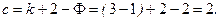 | (12) |
Бивариантность системы означает, что из трех параметров, однозначно характеризующих состояние системы (температура T, общее давление p, концентрация одного из двух компонентов газовой фазы, например %СО, только два могут варьироваться произвольно при неизменных числе и природе равновесных фаз. Если в качестве независимых параметров выбрать внешние, то есть температуру и общее давление, то состав газовой фазы может быть найден из уравнения связи параметров. Этим уравнением является выражение для константы равновесия реакции (11)
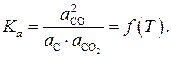 | (13) |
При небольших давлениях термодинамическая активность чистого конденсированного вещества равна единице ( 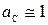 ), а состояние реальных газов можно приближенно описать уравнением Менделеева-Клапейрона, тогда активность компонента газовой смеси
), а состояние реальных газов можно приближенно описать уравнением Менделеева-Клапейрона, тогда активность компонента газовой смеси
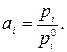 | (14) |
В этом соотношении 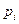 и
и 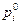 – соответственно парциальное давление компонента в данных условиях и в стандартном состоянии. Поскольку
– соответственно парциальное давление компонента в данных условиях и в стандартном состоянии. Поскольку 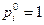 атм, то для компонентов системы (11)
атм, то для компонентов системы (11)
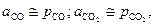 | (15) |
если давления измерены в атмосферах.
Следует обратить внимание на то обстоятельство, что активность газа как величина безразмерная, лишь численно равна его парциальному давлению, выраженному в атмосферах.
С учетом сказанного выражение (13) для константы равновесия принимает вид
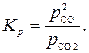 | (16) |
Поскольку парциальное давление газа связано с общим давлением p и его объемным процентом очевидным равенством
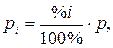 | (17) |
то уравнение (16) может быть представлено в виде
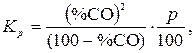 | (18) |
поскольку 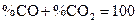 .
.
Константа равновесия химической реакции является функцией температуры, поэтому фиксация T и общего давления p однозначно определяет состав газовой фазы, что и подтверждается правилом фаз Гиббса (12).
Изучаемая реакция протекает с поглощением тепла ( 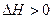 ), и в соответствии с уравнением изобары химической реакции
), и в соответствии с уравнением изобары химической реакции
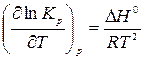 | (19) |
ее константа равновесия увеличивается при возрастании температуры. Поэтому с ростом температуры при постоянном давлении происходит увеличение содержания СО в равновесной газовой фазе, то есть происходит смещение равновесия в сторону образования продукта реакции. Сказанное иллюстрирует рис. 2, на котором приведена температурная зависимость равновесного содержания СО в газовой фазе при различных давлениях в системе. Из анализа уравнения (18) следует, что с увеличением общего давления p имеет место снижение концентрации монооксида углерода при постоянной температуре.
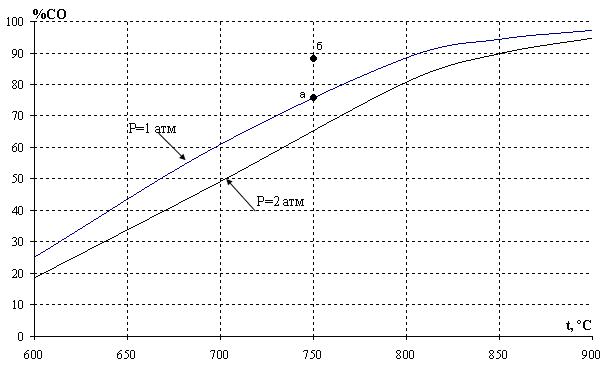
Рис.2. Зависимость равновесного содержания монооксида углерода от температуры при различных давлениях
Отмеченные выше закономерности находятся в соответствии с принципом смещения равновесия Ле-Шателье, согласно которому в равновесной системе при изменении внешних параметров развиваются процессы, стремящиеся ослабить внешнее воздействие. Так, росту температуры при постоянном давлении соответствует развитие эндотермического процесса, то есть прямой реакции (11), а при изотермическом увеличении внешнего давления в системе протекает обратный процесс ( 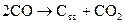 ), сопровождающийся уменьшением числа газовых молей.
), сопровождающийся уменьшением числа газовых молей.
Возможность протекания реакции при фиксированной температуре в заданных условиях определяют по уравнению изотермы. Так, для условий точки б (рис. 2) исходное содержание монооксида углерода (%СОб) превышает равновесное (%СОа), поэтому величина ∆G для реакции (11)
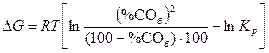 | (20) |
оказывается положительной. Другими словами, в условиях, характеризуемых параметрами точки «б», протекание прямой реакции невозможно, поэтому область, расположенная над изобарой pа, отвечает устойчивому существованию твердого углерода.
Расчет зависимости концентрации СО от температуры при постоянном давлении может быть проведен по уравнению (18) для чего необходимо рассчитать Kp при различных температурах с помощью выражения:
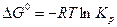 . . | (21) |
ΔG0 находится по известному соотношению
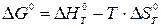 | (22) |
Тепловой эффект реакции и изменение энтропии в ходе реакции при заданной температуре рассчитывают по уравнениям:
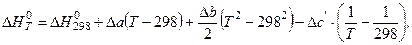 | (23) |
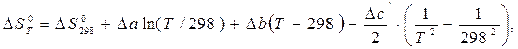 | (24) |
используя справочные данные о теплотах образования, энтропии и теплоемкостях реагентов (прил. 1).
Среднюю величину теплового эффекта реакции в изученном интервале температур определяют графически по методике, приведенной в прил. 2.
Таблица 1
Результаты работы
 | T, K | %CO |  | 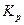 | 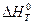 , ,  |  , , 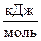 | ||
| (%CO)оп ± ±Δ(%CO) | %СОрасч | 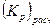 | 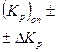 | |||||
По данным таблицы 1 строят график зависимости 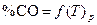 и формулируют общие выводы по результатам работы.
и формулируют общие выводы по результатам работы.
Вопросы для самоконтроля
1. Что означает термин «число степеней свободы (с)» равновесной системы; какие данные необходимы для расчета с?
2. Углерод, растворенный в железе, реагирует с СО2 по реакции 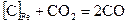 .
.
Определите число степеней свободы системы.
3. Какое состояние называют стандартным для компонента газовой смеси и для чистого конденсированного вещества?
4. Используя уравнение изобары, докажите, что равновесие эндотермической реакции смещается с ростом температуры при постоянном давлении в сторону образования продуктов реакции.
5. При давлении 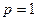 атм и температуре Т равновесное содержание СО в газовой фазе составило 40%. Возможно ли протекание реакции газификации, если при заданных р и Т исходная газовая смесь содержит 2 моля СО2 и 3 моля СО?
атм и температуре Т равновесное содержание СО в газовой фазе составило 40%. Возможно ли протекание реакции газификации, если при заданных р и Т исходная газовая смесь содержит 2 моля СО2 и 3 моля СО?
6. Поясните принцип работы газоанализатора; как рассчитывается концентрация монооксида углерода в газовой фазе?
Работа № 2. ИЗУЧЕНИЕ УПРУГОСТИ ДИССОЦИАЦИИ CaCO3
Целью работы является изучение температурной зависимости упругости диссоциации карбоната кальция и определение теплового эффекта реакции диссоциации CaCO3.
Процессы диссоциации карбонатов имеют большое распространение в металлургии, например, в процессах обжига известняка; разложения известняка в доменной печи, где он употребляется в качестве флюса.
Теоретическая часть
Карбонат кальция, являющийся основной составной частью мела, известняка, мрамора, диссоциирует по реакции
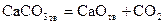 . . | (25) |
Будем считать, что система состоит из чистых CaCO3, CaO и CO2 и между ними протекает только реакция (25).
Равновесное давление двуокиси углерода 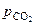 над карбонатом называют его упругостью диссоциации.
над карбонатом называют его упругостью диссоциации.
Число параметров, определяющих состояние равновесия системы, можно найти по правилу фаз Гиббса:
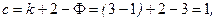 | (26) |
где – k число независимых компонентов в системе; Ф – число фаз.
Система обладает одной степенью свободы, то есть из двух параметров, определяющих состояние системы ( 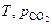 ), один можно изменять произвольно, не меняя количества и природы фаз, характерных для равновесия данной системы. Удобнее в качестве независимой переменной выбрать температуру, тогда
), один можно изменять произвольно, не меняя количества и природы фаз, характерных для равновесия данной системы. Удобнее в качестве независимой переменной выбрать температуру, тогда 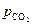 будет её однозначной функцией. Найдем эту функциональную зависимость.
будет её однозначной функцией. Найдем эту функциональную зависимость.
Константа равновесия реакции (25) запишется так:
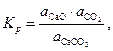 | (27) |
где 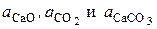 – активности соответствующих реагентов.
– активности соответствующих реагентов.
Известно, что карбонат и оксид кальция весьма мало взаимно растворимы. Поэтому обычно оксид и карбонат находятся в виде самостоятельных твердых фаз, и при небольших давлениях 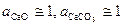 . Активность газообразного СО2 (
. Активность газообразного СО2 ( 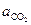 ) определяется соотношением фугитивностей
) определяется соотношением фугитивностей  :
:
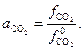 | (28) |
Если давление измерять в атмосферах, то фугитивность в стандартном состоянии 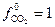 атм и
атм и 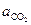 будет численно равна равновесной фугитивности
будет численно равна равновесной фугитивности 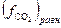 . Поскольку в наших условиях СО2 можно считать идеальным газом, то
. Поскольку в наших условиях СО2 можно считать идеальным газом, то 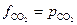 . Таким образом:
. Таким образом:
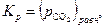 | (29) |
то есть константа равновесия реакции (25) численно равна упругости диссоциации CaCO3, если последняя выражена в атмосферах.
Для анализа зависимости 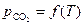 воспользуемся уравнением изобары химической реакции
воспользуемся уравнением изобары химической реакции
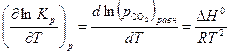 | (30) |
Для процесса диссоциации тепловой эффект 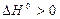 , поэтому упругость диссоциации растет с увеличением температуры. Изменение упругости диссоциации с температурой показано на рис. 4.
, поэтому упругость диссоциации растет с увеличением температуры. Изменение упругости диссоциации с температурой показано на рис. 4.
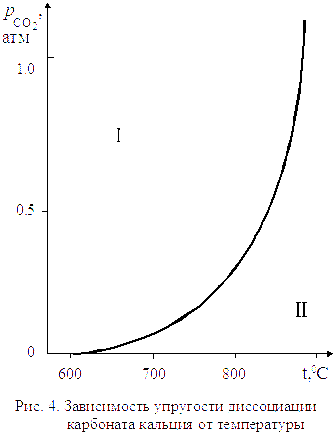 Линия на рис. 4 характеризует условия равновесного сосуществования трех фаз:
Линия на рис. 4 характеризует условия равновесного сосуществования трех фаз: 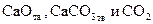 . Если начать изменять не один параметр, как разрешает правило фаз Гиббса, а два, то есть произвольно изменять и температуру, и давление, равновесие системы будет нарушено. Области I и II на графике характеризуют условия равновесного сосуществования уже только двух фаз (одной твердой и газообразной).
. Если начать изменять не один параметр, как разрешает правило фаз Гиббса, а два, то есть произвольно изменять и температуру, и давление, равновесие системы будет нарушено. Области I и II на графике характеризуют условия равновесного сосуществования уже только двух фаз (одной твердой и газообразной).
Для области I характерны давления СО2 бόльшие, чем равновесные значения.
Следовательно, по уравнению изотермы 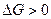 :
:
  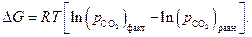 | (31) |
Отсюда можно заключить, что в данных условиях протекает процесс карбонизации
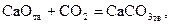 | (32) |
а прямой процесс (диссоциация) невозможен. Иначе говоря, в области I устойчивой фазой является карбонат кальция. Таким образом, если при 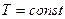 величина
величина 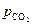 станет больше, чем
станет больше, чем 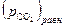 , то это приведет к исчезновению оксидной фазы.
, то это приведет к исчезновению оксидной фазы.
Проведя аналогичные рассуждения для области II, где 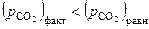 , можно заключить, что при давлениях ниже равновесного
, можно заключить, что при давлениях ниже равновесного 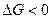 и развитие процесса диссоциации возможно. Устойчивой фазой является в области II оксид кальция
и развитие процесса диссоциации возможно. Устойчивой фазой является в области II оксид кальция 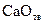 .
.
Поскольку упругость диссоциации, выраженная в атмосферах, численно равна константе равновесия реакции, то ее значение можно теоретически рассчитать по уравнениям (21–24).
Величину теплового эффекта при данной температуре ( 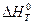 ) можно рассчитать по уравнению Кирхгофа (23).
) можно рассчитать по уравнению Кирхгофа (23).
Среднюю величину теплового эффекта реакции в изученном интервале температур ( 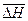 ) можно также оценить по опытным значениям константы равновесия при разных температурах (см. прил.2).
) можно также оценить по опытным значениям константы равновесия при разных температурах (см. прил.2).
При анализе экспериментальных данных и их сопоставлении с рассчитанными по уравнениям (21–24) следует иметь в виду, что на величину упругости диссоциации оказывает влияние дисперсность твердых фаз. При измельчении твердой фазы возрастает ее энергия Гиббса, поскольку увеличивается доля частиц, располагающихся на поверхности кристаллов и обладающих избытком энергии. Принимая во внимание, что общее изменение энергии Гиббса по реакции равно
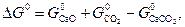 | (33) |
можно заключить, что при измельчении исходной фазы – карбоната ( 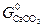 растет) величина
растет) величина 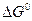 уменьшается, а при измельчении продукта реакции (растет
уменьшается, а при измельчении продукта реакции (растет 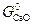 )
) 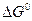 увеличивается. Соответственно, в первом случае
увеличивается. Соответственно, в первом случае 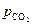 растет, а во втором падает, поскольку
растет, а во втором падает, поскольку
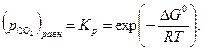 | (34) |
Методика и порядок проведения опытов
Для определения упругости диссоциации CaCO3 в работе используется статический метод. Суть его заключается в непосредственном измерении при данной температуре равновесного давления СО2 в установке.
Схема установки представлена на рис. 5. В электрическую печь сопротивления 1 помещают кварцевую ампулу 2, в которую помещена навеска карбоната 3. Перед началом нагрева печи из ампулы откачивают воздух форвакуумным насосом 4.
После выключения насоса в него надо обязательно запустить воздух с помощью крана 5. |
Кран 5 может быть заменен струбцинами, пережимающими шланги. После этого задатчиком терморегулятора 6 устанавливают первую заданную температуру. Когда заданная температура достигнута (при этом лампочка на терморегуляторе начнет мигать), делают выдержку не менее 10 минут и измеряют давление СО2 в системе с помощью манометра 8. Изотермическая выдержка системы проводится для достижения системой равновесия. При этом, по мере развития реакции, изменяется (увеличивается) давление, а объем реакционного пространства остается постоянным. Следовательно в данном случае процесс проходит при постоянном объеме(V=const). Измеряемая в процессе работы 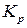 определяется равновесным составом, который не зависит от пути процесса, а определяется элементным составом системы, давление и температурой. Потому
определяется равновесным составом, который не зависит от пути процесса, а определяется элементным составом системы, давление и температурой. Потому 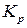 определенную в ходе работы можно анализировать с помощью уравнения изобары и сравнивать с рассчитанной.
определенную в ходе работы можно анализировать с помощью уравнения изобары и сравнивать с рассчитанной.
Измерение упругости диссоциации карбоната кальция следует провести при 4-6 температурах по указанию преподавателя.
Обработка результатов
После проведения опытов строят график 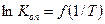 и определяют средний тепловой эффект реакции
и определяют средний тепловой эффект реакции 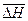 в изученном интервале температур (см. прил. 2).
в изученном интервале температур (см. прил. 2).
Затем по уравнениям (21–24) рассчитывают теоретические значения упругости диссоциации CaCO3, а по уравнению (23) – величины теплового эффекта реакции при заданных температурах.
В данной работе, как правило, систематическая погрешность измерений существенно превосходит случайную. Оценить систематическую погрешность можно путем сравнения полученных экспериментальных данных с результатами расчетов, в которых использованы справочные данные. Причем экспериментальное значение среднего теплового эффекта реакции ( 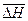 ) следует сравнивать со средним арифметическим значением теоретически найденных тепловых эффектов.
) следует сравнивать со средним арифметическим значением теоретически найденных тепловых эффектов.
В работе следует оценить абсолютные и относительные погрешности определения 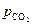 и
и 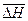 и, оценив целесообразное число значащих цифр в записи результатов измерений, заполнить таблицы 2 и 3.
и, оценив целесообразное число значащих цифр в записи результатов измерений, заполнить таблицы 2 и 3.
Таблица 2
Теоретические значения
| № опыта | t, ºС | Т, К | Теоретические значения | ||
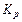 | 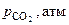 | 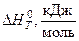 | |||
Таблица 3
Результаты работы
| t, ºС | Т, К | Опытные значения | ||||
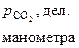 | 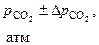 | 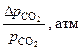 | 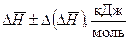 | 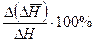 | ||
По данным таблицы строят графики зависимостей 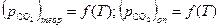 . Делают выводы по полученным результатам. Указывают основные источники погрешностей.
. Делают выводы по полученным результатам. Указывают основные источники погрешностей.
Вопросы для самоконтроля
- Что называется упругостью диссоциации карбоната?
- Докажите, используя правило фаз Гиббса, что упругость диссоциации CaCO3 есть однозначная функция температуры?
- Что произойдет с термодинамической системой, если произвольно изменять бòльшее число параметров, чем позволяет правило фаз Гиббса?
- Как температура влияет на упругость диссоциации?
- Как определить направление процесса диссоциации карбоната, зная температуру и фактическое давление СО2 в системе?
- Как дисперсность твердых фаз влияет на упругость диссоциации?
- В чем состоит суть статического метода определения упругости диссоциации?
Теоретические сведения
Растворение одних веществ в других сопровождается тепловыми эффектами. Связано это с тем, что энергия межчастичного взаимодействия в чистых веществах ( 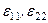 ) и в образованном из них растворе отличаются, то есть
) и в образованном из них растворе отличаются, то есть 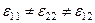 .
.
В теории растворов принято называть растворителем компонент с большей концентрацией, а растворенным веществом – компонент с меньшей концентрацией. В зависимости от условий образования раствора различают два вида теплот растворения. Теплоту, которая выделяется или поглощается при растворении одного моля вещества (при постоянных температуре и давлении) в чистом растворителе, взятом в количестве, необходимом для получения раствора заданного состава, называют интегральной теплотой растворения ( 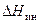 ).
).
Дифференциальной теплотой растворения ( 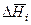 ) называют тепловой эффект растворения бесконечно малого количества вещества в растворе заданного состава, отнесенный к 1 молю растворяемого вещества. Дифференциальную теплоту нецелесообразно измерять непосредственно, ее рассчитывают по интегральным теплотам растворения. Для этой цели строят график зависимости теплового эффекта образования раствора
) называют тепловой эффект растворения бесконечно малого количества вещества в растворе заданного состава, отнесенный к 1 молю растворяемого вещества. Дифференциальную теплоту нецелесообразно измерять непосредственно, ее рассчитывают по интегральным теплотам растворения. Для этой цели строят график зависимости теплового эффекта образования раствора 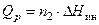 от числа молей растворенного вещества
от числа молей растворенного вещества 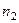 при постоянном количестве растворителя. Угол наклона касательной, проведенной к кривой при заданном значении
при постоянном количестве растворителя. Угол наклона касательной, проведенной к кривой при заданном значении 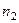 , дает дифференциальную теплоту растворения, так как
, дает дифференциальную теплоту растворения, так как
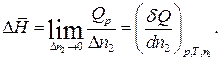 | (35) |
Можно предположить, что система поглощает теплоту для преодоления энергии межчастичного взаимодействия в растворяемом веществе при его растворении. Однако, наряду с процессом «разрыва» химических связей обычно происходит и другой, называемый сольватацией. Сольватация представляет собой сильное взаимодействие растворяемого вещества с растворителем и сопровождается выделением тепла. Если растворителем является вода, сольватация называется гидратацией.
Роль подобного взаимодействия растворителя с растворяемым веществом можно показать на примере растворения хлорида натрия в воде. В кристаллической решетке хлорида натрия катион натрия и анион хлора связаны друг с другом гетерополярной (ионной) связью. Энергия, необходимая для их разделения, настолько велика, что такие неполярные растворители как бензол, четыреххлористый углерод, не растворяют хлорид натрия. Однако растворитель, подобный воде, молекулы которой обладают высокой диэлектрической постоянной и большим дипольным моментом, сильно «притягивается» как к ионам натрия, так и к ионам хлора. В итоге происходит сольватация ионов, которая сопровождается значительным уменьшением энергии системы. Если энергия, требуемая для отрыва ионов от кристалла, приблизительно равна энергии сольватации, как в случае растворения NaCl в воде, значение суммарного теплового эффекта близко к нулю. При растворении NaCl в воде при 25ºС наблюдается лишь небольшое охлаждение, величина 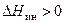 . При растворении же в воде Na2SO4 при 25ºC выделяется тепло, потому что теплота гидратации (
. При растворении же в воде Na2SO4 при 25ºC выделяется тепло, потому что теплота гидратации ( 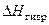 ) больше энергии отрыва ионов от кристалла.
) больше энергии отрыва ионов от кристалла.
Таким образом, растворение твердой соли в воде может быть представлено как результат наложения двух процессов. Переходя в жидкий раствор, соль изменяет агрегатное состояние, становясь жидкой. При этом система поглощает тепло, равное теплоте плавления соли ( 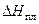 ). Далее ионы соли после «плавления» смешиваются с молекулами воды, причем тепловой эффект смешения (
). Далее ионы соли после «плавления» смешиваются с молекулами воды, причем тепловой эффект смешения ( 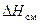 ) для солей, как правило, отрицателен (
) для солей, как правило, отрицателен ( 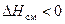 ). Другими словами, знак суммарного теплового эффекта (интегральной теплоты растворения) зависит от соотношения величин
). Другими словами, знак суммарного теплового эффекта (интегральной теплоты растворения) зависит от соотношения величин 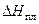 и
и 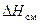 , так как
, так как
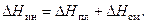 | (36) |
Если растворять соли с общим катионом или анионом, то величина теплового эффекта будет определяться природой второго иона, входящего в соединение. Чем он сильнее (сила иона оценивается по отношению заряда к радиусу), тем прочнее связан в соединении, а значит, тем больше энергии требуется затратить на плавление (разрушение решетки соли). С другой стороны, более сильный ион образует более прочные связи с диполями воды, что увеличивает теплоту смешения. Общее изменение теплового эффекта при переходе от одной соли к другой будет определяться изменением теплот плавления и гидратации.
Методика проведения опытов
Для определения интегральной теплоты растворения используется простейший калориметр, состоящий из внутреннего 3 (рис. 6) и наружного стакана 1. Сверху стаканы закрыты крышкой из материала с малой теплопроводностью. В крышке имеются два отверстия: одно для воронки, через которую засыпают навеску соли, через второе в термостат вводится термопарный датчик 4 (он позволяет находить изменение температуры в процессе растворения соли). Перемешивание жидкости в стакане 3 осуществляется магнитной мешалкой 2. Величины ЭДС датчиков регистрируются цифровым вольтметром 5. Показания последнего заносятся в таблицу первичной информации « 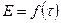 ».
».
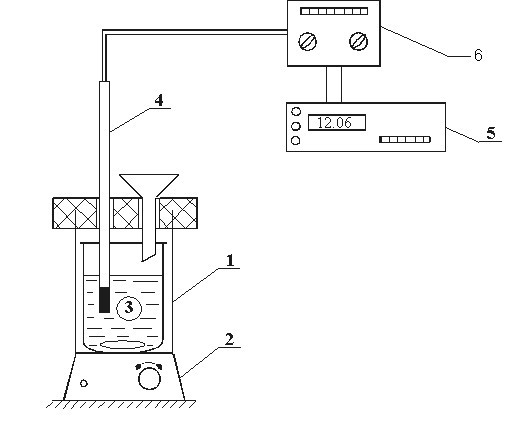
Рис.6. Схема установки для определения теплоты растворения: 1 – калориметр; 2 – магнитная мешалка; 3 – стеклянный стакан; 4 – термобатарея; 5 – вольтметр; 6 – усилитель сигнала
Используемые медь‑константановые термопары обладают линейной зависимостью ЭДС от температуры, и значение коэффициента 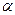 в уравнении
в уравнении
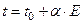 | (37) |
указывается на используемом приборе. В этом уравнении величина 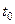 соответствует температуре спаев термопар, находящихся вне калориметра, а
соответствует температуре спаев термопар, находящихся вне калориметра, а 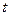 – температура «рабочих» спаев, помещенных в раствор.
– температура «рабочих» спаев, помещенных в раствор.
Для проведения опытов необходимо приготовить навески солей в расчете на 300 мл воды при конечной концентрации соли, равной 0,20 М. Используемые соли должны быть сухими и тщательно растертыми в фарфоровой ступке. Наличие крупных кусочков соли увеличивает время растворения и приводит к дополнительным ошибкам в определении теплоты растворения.
После приготовления требуемых навесок солей во внутренний стакан наливают 300 мл дистиллированной воды, закрывают термостат крышкой, включают магнитную мешалку и фиксируют в течение 7 минут показания приборов. При использовании цифрового вольтметра 5 удобнее записывать в таблицу величины через каждую минуту. Далее, на седьмой минуте следует засыпать соль и продолжать фиксировать показания прибора. После введения соли рекомендуется 4-6 замеров сделать через 30 секунд, а остальные – через минуту, закончив замеры через 10-12 минут после засыпки соли.
Расчет интегральной теплоты растворения производят по формуле
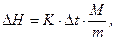 | (38) |
где 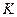 – постоянная калориметра;
– постоянная калориметра; 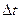 – изменение температуры при растворении;
– изменение температуры при растворении; 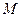 – молекулярный вес соли;
– молекулярный вес соли; 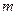 – навеска соли в граммах.
– навеска соли в граммах.
Постоянная калориметра характеризует количество тепла, необходимое для повышения температуры внутри калориметра на один градус. Её определяют, внося в калориметр фиксированное количество тепла (например, пропуская через электрическое сопротивление ток в течение определенного времени) и определяя одновременно повышение температуры. Численное значение постоянной дается преподавателем или определяется студентами по величине 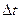 растворения «стандартной» соли.
растворения «стандартной» соли.
Изменение температуры 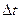 при растворении определяют графически. Поскольку температура раствора пропорциональна величине измеряемой ЭДС, строят график непосредственно в координатах «
при растворении определяют графически. Поскольку температура раствора пропорциональна величине измеряемой ЭДС, строят график непосредственно в координатах « 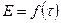 ».
».
Из графика следует, что время опыта делится на три периода. В первом периоде до момента засыпки соли ( 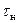 ) наблюдается равномерное увеличение температуры (ЭДС) за счет выделения тепла при вращении мешалки в воде. При добавлении соли в момент
) наблюдается равномерное увеличение температуры (ЭДС) за счет выделения тепла при вращении мешалки в воде. При добавлении соли в момент 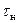 наблюдается интенсивное снижение температуры и по окончании растворения (
наблюдается интенсивное снижение температуры и по окончании растворения ( 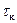 ) наблюдается ее монотонное увеличение.
) наблюдается ее монотонное увеличение.
Очевидно, что в процессе растворения раствор обменивается теплом со средой, поэтому для расчета 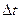 необходимо по опытным данным построить гипотетическую зависимость
необходимо по опытным данным построить гипотетическую зависимость 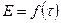 для «мгновенного» растворения.
для «мгновенного» растворения.
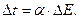 | (39) |
С этой целью определяют время конца растворения 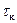 как точку, в которой зависимость «
как точку, в которой зависимость « 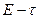 » становится линейной. По графику находят середину второго периода и восстанавливают перпендикуляр к оси абсцисс до пересечения с продолжением линии р
» становится линейной. По графику находят середину второго периода и восстанавливают перпендикуляр к оси абсцисс до пересечения с продолжением линии р

