Метод неопределенного интегрирования заменой переменной. Метод неопределенного интегрирования подведением под знак дифференциала.

Сущность метода заключается в том, что путем введения новой переменной интегрирования (т.е. подстановки) удается свести заданный интеграл к новому интегралу, который является табличным или легко находится другим способом. Общих методов подбора подстановок не существует. Рассмотрим некоторые варианты подстановок.

Линейные подстановки

При сведении данного интеграла к табличному часто используются преобразования дифференциала (операция «подведения под знак дифференциала»).

I. Под знак дифференциала, стоящего в интеграле, можно ввести любое постоянное слагаемое.

При любой постоянной а будет

.

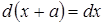Поэтому

.

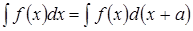Пример

1. ;

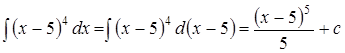II. Под знак дифференциала, стоящего в интеграле, можно ввести любой постоянный множитель, разделив на него интеграл.

Известно, если а − постоянно, то

.

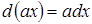Тогда

.

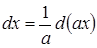Поэтому

.

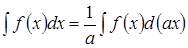Пример

1. ;

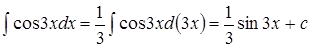В некоторых случаях применяют оба приема вместе:

,

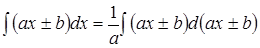где а и b − постоянные.

Пример

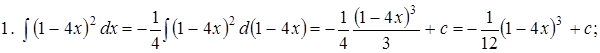
5. Теорема о непосредственном интегрировании подыинтегральной функции y=f(ax+b). О выражении интегралов через элементраные функции. Неберущиеся интегралы.

Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

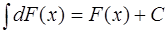Действительно, поскольку

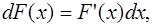то .

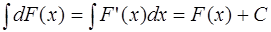Непосредственное интегрирование

В некоторых случаях подынтегральную функцию удаётся представить в виде линейной комбинации конечного числа функций, интегралы от которых являются табличными. Тогда говорят, что неопределённый интеграл вычисляется непосредственно или методом разложения.

Пример.

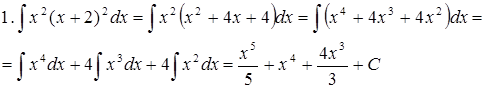
Подстановка вида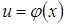

Если под знаком интеграла стоит сложная функция, умноженная на производную от внутренней функции, т.е. интеграл имеет вид:

,

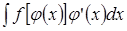то этот интеграл можно упростить, если заменить внутреннюю функцию новой переменной .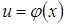

Тогда получим

.

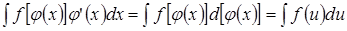В данном случае была применена операция «подведения под знак дифференциала» ( ).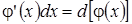

Для применения подстановки 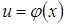существует следующее правило.

Правило.

Чтобы найти интеграл 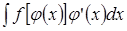, надо

1) переписать интеграл в виде

;

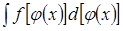2) сделать замену 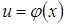, что приведет к интегралу

;

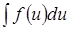3) найти последний интеграл;

4) в полученном ответе произвести обратную замену u на .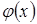

Пример

1.

;

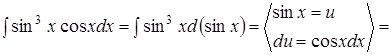
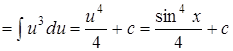Подстановка вида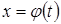

Пусть требуется найти интеграл

.

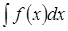Иногда бывает целесообразно при вычислении такого интеграла, в котором независимой переменой является х, сделать подстановку 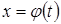. Преобразуя подынтегральное выражение путем подстановки, имеем

,

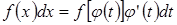так как .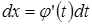

В результате получаем формулу интегрирования подстановкой :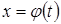

.

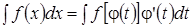Замечание.

Функция 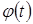выбирается так, чтобы интеграл в правой части равенства был более простым, чем первоначальный.

Сформулируем правило подстановки.

Правило.

Чтобы найти интеграл 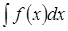, надо

1) перейти к новой переменной t, связанной с х выражением ;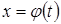

2) выразить через t все подынтегральное выражение :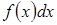

;

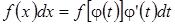3) найти новый интеграл:

;

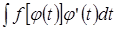4) в полученном ответе произвести обратную замену 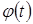на х.

Пример

1.

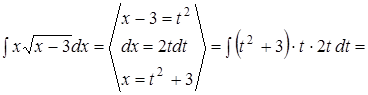
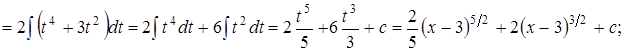
Из основных правил дифференцирования следует, что производная элементарной функции всегда являются элементарной функцией.

Существенно, что операция интегрирования таким свойством не обладает:

Первообразная элементарной функции не всегда является элементарной функцией.

Пример. Рассмотрим функцию 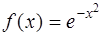. Её график изображён на рис. 1.4.

Эта функция непрерывна на всей числовой прямой. Поэтому она имеет первообразную функцию, определённую тоже на всей числовой прямой. Однако эта первообразная не является элементарной функцией.

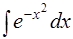- «неберущийся» интеграл

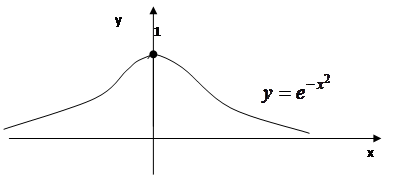
Рис.1.4.

На рисунке 1.5 изображена функция 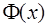- та первообразная функции 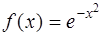, график которой проходит через начало координат.

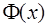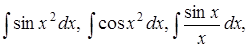
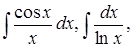
Функция не является элементарной. Однако её значения известны во всех точках числовой оси. Отметим, что «неберущимися» являются также интегралы 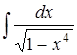и многие другие. Однако первообразные функций 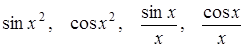, 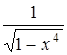хорошо изучены – не менее подробно, чем синус или логарифм – это функции принципиально новой, неэлементарной природы

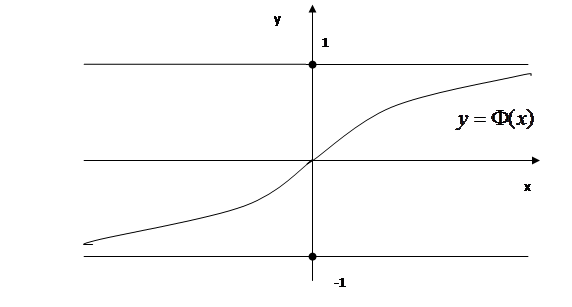
Рис. 1.5.

Умение выражать первообразные элементарных функций через элементарные (в тех случаях, когда это возможно) или, как принято говорить, умение «брать интегралы» - своего рода искусство. Овладеть им можно изучив некоторые методы интегрирования, а затем взяв большое количество интегралов.

Однако значение этого искусства (при всей его важности) не следует преувеличивать. Очень часто в теории и приложениях приходится иметь дело именно с «неберущимися» интегралами. В математическом анализе имеются надёжные средства их исследования и вычисления.