Дивергенция и ротор векторного поля
Определение дивергенции выглядит так:
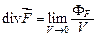 ,
,
где 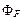 — поток векторного поля
— поток векторного поля 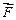 через сферическую поверхность площадью
через сферическую поверхность площадью 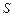 , ограничивающую объем
, ограничивающую объем 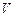 .
.
Более общим является определение, когда форма области с поверхностью 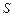 и объемом
и объемом 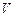 допускается любой. Единственное требование – нахождение поверхности внутри сферы радиусом, стремящимся к нулю, – не привязано к определенным координатам. Допустим, что векторное поле дифференцируемо в некоторой области. Тогда в трехмерном декартовом пространстве дивергенция поля
допускается любой. Единственное требование – нахождение поверхности внутри сферы радиусом, стремящимся к нулю, – не привязано к определенным координатам. Допустим, что векторное поле дифференцируемо в некоторой области. Тогда в трехмерном декартовом пространстве дивергенция поля 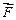 будет определяться выражением:
будет определяться выражением:
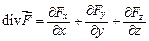 .
.
Это же выражение можно записать с использованием оператора набла: 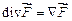 .
.
Многомерная, а также двумерная и одномерная дивергенция определяется в декартовых координатах в пространствах соответствующей размерности совершенно аналогично (в верхней формуле меняется лишь количество слагаемых, а нижняя остается той же, подразумевая оператор набла подходящей размерности).
С точки зрения физики, дивергенция векторного поля является показателем того, в какой степени данная точка пространства является источником или стоком этого поля:
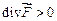 – точка поля является источником;
– точка поля является источником;
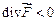 – точка поля является стоком;
– точка поля является стоком;
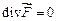 – стоков и источников нет, либо они компенсируют друг друга.
– стоков и источников нет, либо они компенсируют друг друга.
Например, если в качестве векторного поля взять совокупность направлений наискорейшего спуска на земной поверхности, то дивергенция покажет местоположение вершин и впадин, причем на вершинах дивергенция будет положительна (направления спуска расходятся от вершин), а на впадинах отрицательная (ко впадинам направления спуска сходятся).
Еще одним, быть может, несколько схематическим, примером может служить озеро (для простоты — постоянной единичной глубины со всюду горизонтальной скоростью течения воды, не зависящей от глубины, давая, таким образом, двумерное векторное поле на двумерном пространстве). В такой модели родники, бьющие из дна озера, будут давать положительную дивергенцию поля скоростей течения, а подводные стоки (пещеры, куда вода утекает) — отрицательную дивергенцию.
Ротор векторного поля — вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру 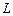 плоской площадки
плоской площадки 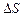 , перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:
, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:
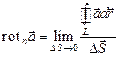 . (1.14)
. (1.14)
Нормаль 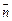 к площадке направлена так, чтобы при вычислении циркуляции обход по контуру
к площадке направлена так, чтобы при вычислении циркуляции обход по контуру 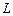 совершался против часовой стрелки.
совершался против часовой стрелки.
В трехмерной декартовой системе координат ротор вычисляется следующим образом:
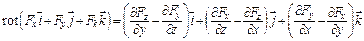 .
.
Когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.
Например, если в качестве векторного поля взять поле скоростей ветра на Земле, то в северном полушарии для антициклона, вращающегося по часовой стрелке, ротор будет направлен вниз, а для циклона, вращающегося против часовой стрелки — вверх. В тех местах, где ветры дуют прямолинейно и с одинаковой скоростью, ротор будет равен нулю (у неоднородного прямолинейного течения ротор ненулевой).
1.15. Дивергенция вектора 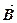 магнитного поля
магнитного поля
Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора  не имеют ни начала, ни конца. Поэтому поток вектора
не имеют ни начала, ни конца. Поэтому поток вектора  через замкнутую поверхность должен быть равен нулю. Таким образом, для любого магнитного поля и произвольной замкнутой поверхности
через замкнутую поверхность должен быть равен нулю. Таким образом, для любого магнитного поля и произвольной замкнутой поверхности 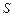 имеет место условие:
имеет место условие:
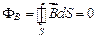 .
.
Эта формула выражает теорему Гаусса для вектора  : поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
Заменив поверхностный интеграл объемным, получим, что
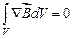 .
.
Условие, к которому мы пришли, должно выполняться для любого произвольно выбранного объема 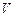 . Это возможно только в том случае, когда подынтегральная функция в каждой точке поля равна нулю. Таким образом, дивергенция вектора
. Это возможно только в том случае, когда подынтегральная функция в каждой точке поля равна нулю. Таким образом, дивергенция вектора  всюду равна нулю:
всюду равна нулю:
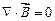 . (1.15)
. (1.15)
Получили теорему Гаусса для поля  в дифференциальной форме.
в дифференциальной форме.
Закон (1.15) является фундаментальным: он справедлив не только для постоянных, но и для переменных магнитных полей.
