Ротор (вихрь) векторного поля

Формула Стокса.

Пусть 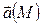- векторное поле, заданное в конечной области G с гладкой (или кусочно-гладкой) границей σ и 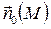- единичный вектор внешней нормали к σ в точке M. Вектор-функция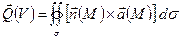

называется циркуляцией поля 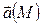по границе области G.

Если существует предел при стягивании объёма V, заключённого внутри 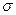в точку :

,

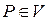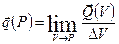то вектор 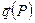называется ротором или вихрем поля 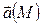в точке 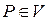и обозначается символом 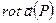. По определению:

.

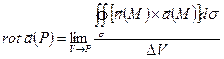это плотность циркуляции векторного поля по границе области.

Пусть в области G задано векторное поле 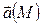. Пусть 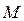- внутренняя точка области G,π –некоторая плоскость, проходящая через эту точку. 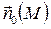- единичный вектор внешней нормали к π, L- замкнутый контур, лежащий в плоскости и ограничивающий область Ф, такую, что 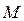- внутренняя точка области Ф. Тогда принимают 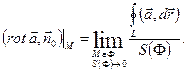(24)

В правую часть формулы (24) входят величины, инвариантные относительно выбора системы координат (циркуляция векторного поля вдоль замкнутого контура и площадь плоской области).

Если компоненты 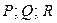поля 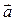имеют непрерывные частные производные по 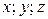, то вектор ротора поля 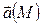вычисляется по формуле:

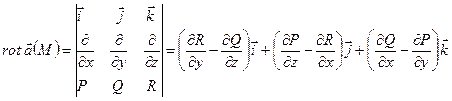. (25)

В частности, для плоского поля : .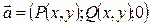

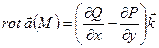Определение 12.Если в каждой точке области выполняется равенство 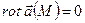, то поле 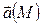называется безвихревым.

Теорема. В односвязной области всякое безвихревое поле потенциально.

.

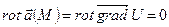Это является необходимым и достаточным условием потенциальности поля 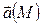в поверхностно односвязной области. Если область не является поверхностно односвязной, то условие 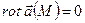не достаточно для потенциальности поля.

Формула Стокса.

Пусть в области G определено векторное поле 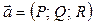. L – замкнутый контур, расположенный в области G. σ – поверхность, ограниченная контуром L, гладкая или кусочно-гладкая. 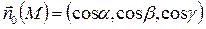- единичный вектор нормали на выбранной стороне поверхности σ . Пусть функции 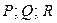непрерывны вместе со своими частными производными. Тогда справедлива формула Стокса:

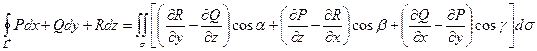. (26)

Ориентация контура L согласована с ориентацией поверхности σ по правилу правого винта. Или:

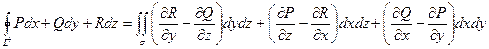. (27)

Левая часть формулы Стокса – это циркуляция векторного поля 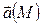вдоль контура L, а правая представляет собой поток через поверхность σ векторного поля 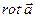. В векторной форме формулу Стокса можно записать так: 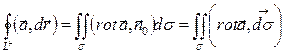. (28)

Физический смысл формулы Стокса: циркуляция векторного поля 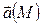вдоль замкнутого контура равна потоку ротора этого поля через произвольную поверхность, натянутую на этот контур.

Формула Стокса остаётся справедливой и в случае, когда поверхность σ является плоской областью, параллельной какой-нибудь координатной плоскости. Тогда формула Стокса превращается в формулу Грина:

.

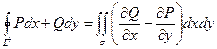Пример 22. Найти ротор векторного поля 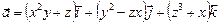и убедиться, что новое поле 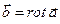является соленоидальным.

Решение. По формуле (25) имеем:

.

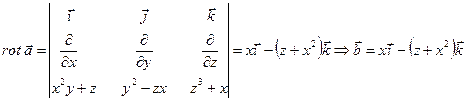Вычислим 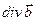по формуле (29): .

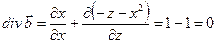Ответ: Так как 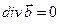, поле 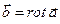является соленоидальным, ч.т.д.

Пример 23. Проверить, является ли потенциальным векторное поле .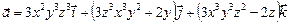

Решение. По формуле (25) имеем:

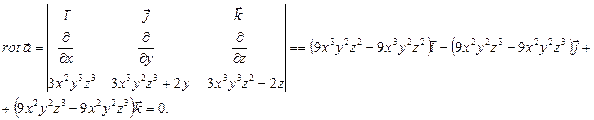
Ответ: данное поле является потенциальным, т.к. .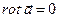

Пример 24.

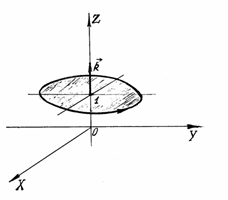
Вычислить циркуляцию векторного поля 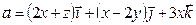по эллипсу 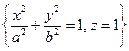. Обход контура против часовой стрелки, если смотреть из точки M(0,0,3). Ответ проверить по формуле Стокса.

Решение. 1) По формуле (7): Ц .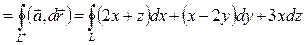

Примем: 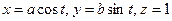, тогда 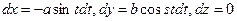, 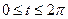. Ц .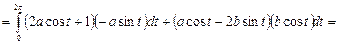

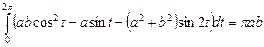2)По формуле Стокса: Ц .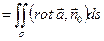

Вычислим 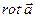по формуле (25): .

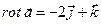В качестве σ выберемплоскость z=1, тогда 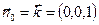и .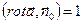

Тогда Ц 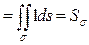. Площадь эллипса с полуосями a и b равна .

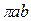Ответ: Ц .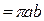

Пример 25.Вычислить циркуляцию векторного поля:

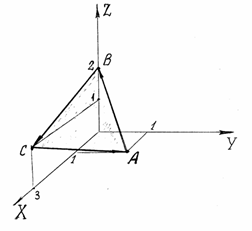
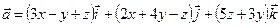по контуру треугольника ABC , где A(1,1,0), B(0,0,2), C(3,0,1), двумя способами: 1) с помощью криволинейного интеграла, 2) по формуле Стокса.

Выяснить, как зависит циркуляция от расположения контура в данном поле.

Решение.

1) По формуле (7): Ц 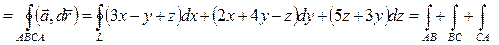(см. рис.17)

Составим уравнения прямых, содержащих стороны треугольника.

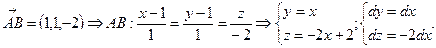
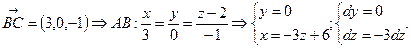
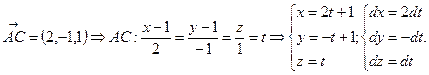
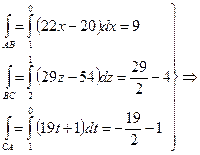Ц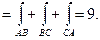

2) Вычислим циркуляцию по формуле Стокса: Ц 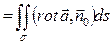. В качестве поверхности σ выберемплоскость треугольника ABC. Тогда 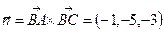. Единичный вектор нормали, составляющий острые углы с осями координат: .

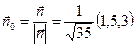Найдём 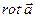по формуле (25): , .

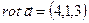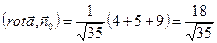Тогда Ц 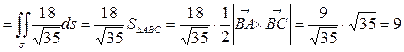, ч.т.д.

3) Исследуем поведение циркуляции при перемещении нашего контура в пространстве. Для этого используем определение скалярного произведения.

Ц 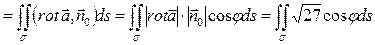, где – угол между векторами и .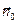

Видим, что циркуляция зависит от этого угла 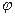. Отсюда следует, что если треугольник ABC перемещается в пространстве параллельно своему исходному положению, то угол 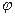не меняется, и циркуляция по контуру остаётся равной 9, а при повороте контура меняется направление вектора 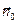, что влечёт изменение циркуляции.

Циркуляция достигнет максимального значения, когда 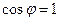, т.е. когда 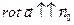. В этом случае Ц .

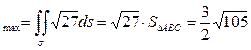Если 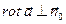, то Ц=0.

Ответ:Ц=9, Ц .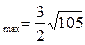

Пример 26.Вычислить циркуляцию векторного поля 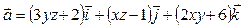вдоль линии L пересечения поверхности 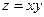и цилиндра 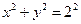, используя формулу Стокса, если нормаль к поверхности образует острый угол с осью OZ.

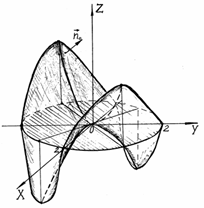Решение.

По формуле Стокса: Ц .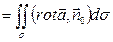

Найдём 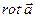по формуле (25): .

Рис18

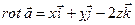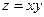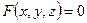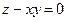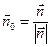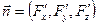Линия L ограничивает часть поверхности гиперболического параболоида . Перепишем это уравнение в неявном виде : . Нормаль к ней получим по формуле: , где . Т.е 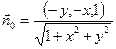. Данный вектор образует острый угол с осью OZ, что и требуется по условию задачи.
Тогда 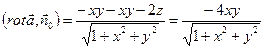, т. к. 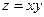из уравнения поверхности. Получаем Ц 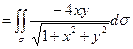- поверхностный интеграл первого рода.

Для его вычисления спроектируем 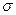на плоскость XOY. Проекцией является круг .

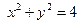Имеем .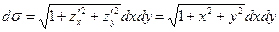

Тогда: Ц .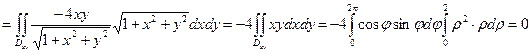

Ответ: Ц=0.

Контрольное задание 9.

1. Вычислить криволинейный интеграл 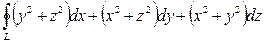, где L – линия пересечения верхней полусферы 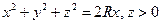с цилиндром 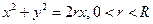. L пробегает против хода часовой стрелки, если смотреть из точки (0,0,3R).

2. Найти циркуляцию векторного поля 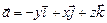вдоль замкнутого контура L, составленного из части винтовой линии 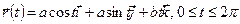и отрезка прямой, соединяющей точки B(a,0,2π) и A(a,0,0). Движение происходит от точки B к A и далее к B.

3. Для векторного поля 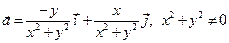вычислить 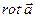, циркуляцию поля 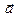вдоль окружности 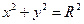и выяснить, является ли поле 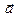потенциальным в области 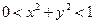; в области ?

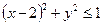4. Найти циркуляцию поля 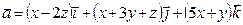вдоль контура треугольника OABO c координатами вершин O(0,0,0), A(1,1,2), B(0,1,2). Ответ проверить с помощью формулы Стокса. Найти максимальное значение циркуляции по данному контуру.