Атом водорода по теории Бора

· Постулаты Бора:

1.Существуют некоторые устойчивые («стационарные») состояния атома, в которых он вопреки классической физике не излучает. Эти стационарные состояния соответствуют движению электронов в атоме по некоторым «разрешенным» орбитам, на которых момент импульса электрона имеет дискретные значения, отвечающие условию

,

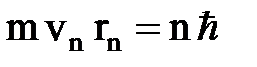где 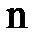- целое положительное число, ( 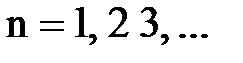), названное квантовым числом, которое можно рассматривать как номер разрешенной орбиты; 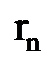- радиус орбиты с номером 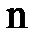; 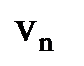- скорость электрона на этой орбите.

2.При переходе электрона с одной разрешенной орбиты на другую атом излучает или поглощает квант электромагнитной энергии, равный

,

где 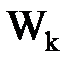- энергия электрона на орбите с номером (квантовым числом) 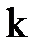, 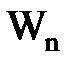- энергия электрона на орбите с номером 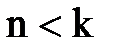; 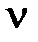- частота электромагнитного излучения.

· Квантование энергии электрона в атоме водорода:

.

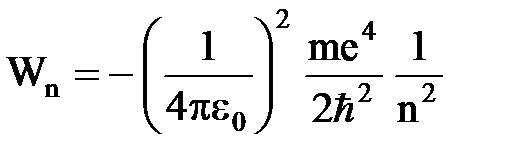Энергия основного состояния атома водорода равна

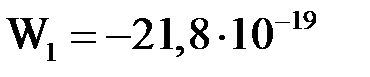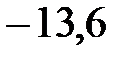Дж = эВ.

При этом радиус первой орбиты составляет .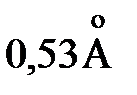

· Сериальная формула Бальмера

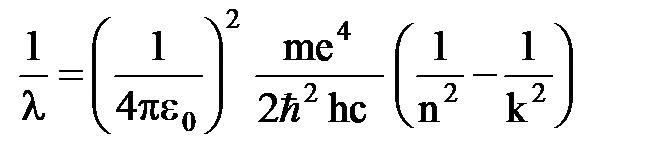или ,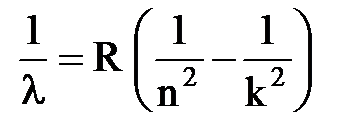

где 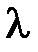- длина волны, соответствующая каждой спектральной линии, 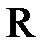- постоянная Ридберга 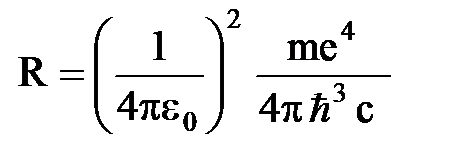; 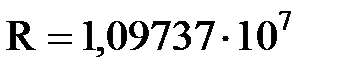м ^-1. Соответственно, для серии Лаймана 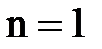, 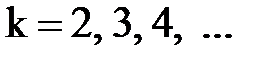; для серии Бальмера 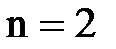, 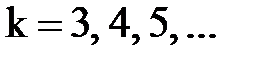; для серии Пашена , .

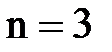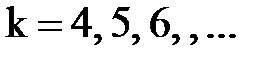Квантово-механическое описание атома водорода

· Стационарное уравнение Шредингера для атома водорода:

.

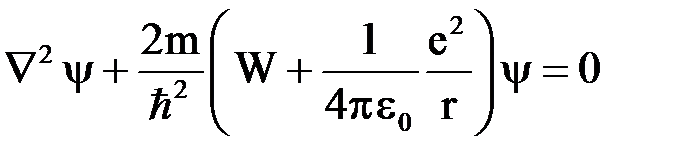· Физический смысл квантовых чисел:

- главное квантовое число :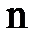

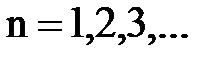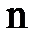; определяет собственные значения энергии электрона в атоме водорода

;

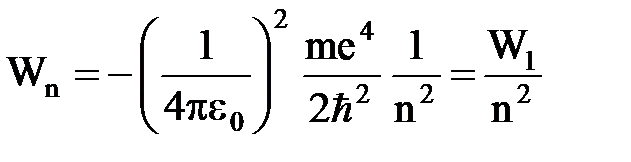- наиболее вероятное удаление электрона от ядра в возбужденном атоме возрастает пропорционально :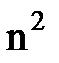

.

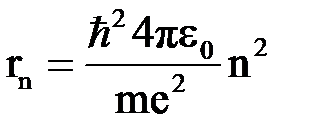· Орбитальное (азимутальное) квантовое число :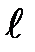

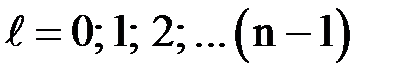; определяет орбитальный механический момент импульса

.

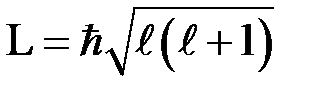Обычно - состояния обозначаются буквами:

						...
s	p	d	f	g	h	...

Из формулы связи орбитальных механического и магнитного моментов ( 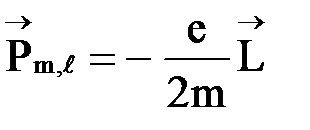) следует квантование орбитального магнитного момента:

,

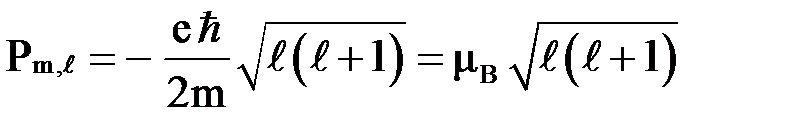где 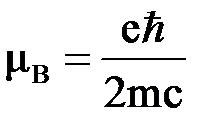- магнетон Бора, 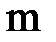- масса электрона;

- правило отбора для квантового числа : .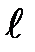

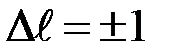· магнитное (орбитальное магнитное) квантовое число :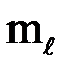

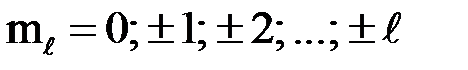; определяет проекцию орбитального механического момента на некоторое произвольно выбранное направление (например, на ось z):

,

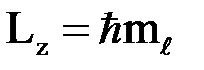где 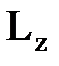- проекция момента импульса на произвольно выбранную ось.

Из квантования проекции орбитального механического моментаследует квантованиепроекции орбитального магнитного момента

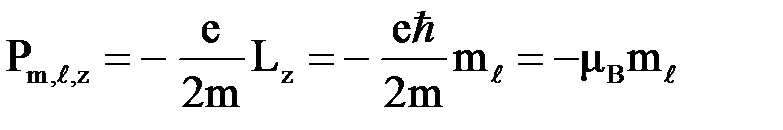
· Спиновое и магнитное спиновые числа:

- спиновое кантовое число 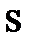: для электрона 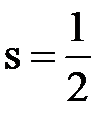; 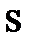определяет собственный механический момент импульса

;

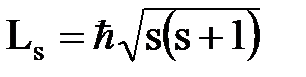- модуль собственного магнитного момента электрона:

,

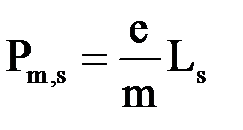- спиновое магнитное квантовое число 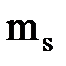; для электрона 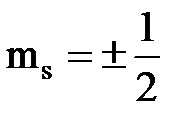; определяет проекцию собственного момента на пространственную ось z:

,

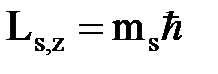- проекция магнитного спинового момента принимает два значения:

,

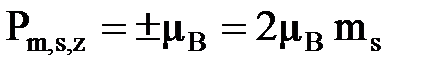· Квантовое число суммарного спин-орбитального момента

;

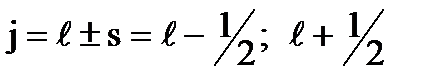суммарный момент

.

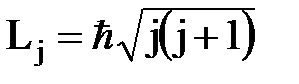Кратность вырождения состояний в атоме водорода с учетом спина

.
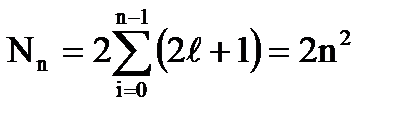