Истечение жидкости через отверстия в тонкой стенке при переменном уровне
Истечение жидкости при переменном уровне встречается пр;: опорожнении и наполнении резервуаров, цистерн, шлюзовых камер, бассейнов и других емкостей. Обычно в этом случае необходимо определить время опорожнения или наполнения емкости.
Рассмотрим случай опорожнения резервуара через донное отверстие в атмосферу (рис. 42). Пусть резервуар призматического сечения и имеет площадь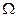 
. Очевидно, движение жидкости будет неустановившимся, так как уровень е течением времени опускается, что вызывает постоянное уменьшение расхода.
Выберем какой-то момент времени, в который уровень жидкости в резервуаре будет у. За бесконечно малый промежуток времени dt уровень жидкости уменьшится на величину dy (за этот промежуток времени движение можно считать установившимся). За что время вытечет объем жидкости, равный
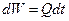, (135)
или
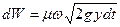. (136)
Выражая тот же объем жидкости через размеры резервуара, имеем
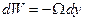. (137)
Знак минус поставлен потому, что dy величина отрицательная (снижение уровня), а объем должен быть величиной положительной.
Приравнивая правые части уравнений (136) и (137), получим
,
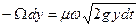откуда
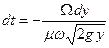. (138)
Интегрируя полученное выражение, найдем время истечения
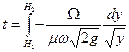, (139)
или, вынося постоянные величины за знак интеграла,
,
.
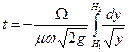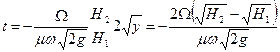Итак, время понижения уровня от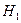 
до 
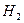
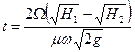. (140)
Время полного опорожнения, т. е. если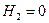 
равно
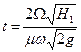. (141)
Рассмотрим случай истечения под уровень (рис. 43). Пусть разность уравнений жидкости в резервуарах равна у, площади поперечного сечения резервуаров соответственно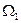 
и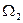 
.
Определим время выравнивания уровней при истечении жидкости через отверстие в тонкой стенке. За бесконечно малый промежуток времени из первого резервуара вытечет объем жидкости
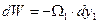, (а)
во втором резервуаре прибудет тот же объем, равный
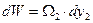, (б)
в то же время
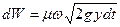. (в)
Из чертежа имеем
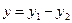
или
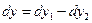, (г)
но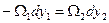 
, откуда
.
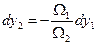Подставим значение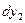 
в уравнение (г)
,
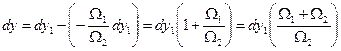откуда
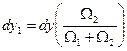. (д)
Подставим значение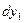 
из выражения (д) в уравнение (а)
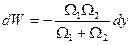
и приравняем правые части полученного уравнения и уравнения (в)
.
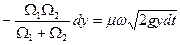Разделим переменные и интегрируем
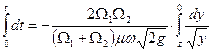
и
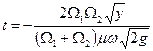; (142)
в частном случае при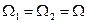 
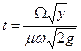. (143)
3.4. Виды насадков и их применение. Истечение жидкости через насадки
Насадкой называется отрезок трубы, длина которого в несколько раз больше внутреннего диаметра. Рассмотрим случай, когда к отверстию в стенке резервуара присоединен насадок диаметром d, равным диаметру отверстия.
На рис. 44 показаны наиболее распространенные виды насадок, применяемые на практике:
а - цилиндрический внешний; б - цилиндрический внутренний; в -конический расходящийся; г - конический сходящийся; д - коноидально-расходящийся; е - коноидальный.
Цилиндрические насадки встречаются в виде деталей гидравлических систем машин и сооружений. Конические сходящиеся и коноидальные насадки применяют для увеличения скорости и дальности полета струи воды (пожарные брандспойты, стволы гидромониторов, форсунки, сопла и др.).
Конические расходящиеся насадки применяют для уменьшения скорости и увеличения расхода жидкости и давления на выходе во всасывающих трубах турбин и др. В эжекторах и инжекторах также имеются конические насадки, как основной рабочий орган. Водопропускные трубы под насыпями дорог (с точки зрения гидравлики) также представляют собой насадки.
Рассмотрим истечение через внешний цилиндрический насадок (рис. 45).
Струя жидкости при входе в насадок сжимается, а потом расширяется и заполняет все сечение. Из насадка струя вытекает полным сечением, поэтому коэффициент сжатия, отнесенный к выходному сечению,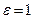 
, а коэффициент расхода
.
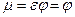Составим уравнение Д. Бернулли для сечений 1-1 и 2-2
,
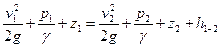где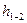 
– потери напора.
Для истечения из открытого резервуара в атмосферу аналогично истечению через отверстие уравнение Д. Бернулли приводится к виду
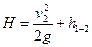. (144)
Потери напора в насадке складываются из потерь па входе и на расширение сжатой струи внутри насадка. (Незначительными потерями в резервуаре и потерями по длине насадка ввиду их малости можно пренебречь.) Итак,
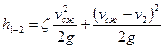. (145)
По уравнению неразрывности можем записать:
,
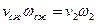откуда
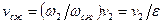. (146)
Подставляя значение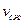 
в уравнение (145), имеем
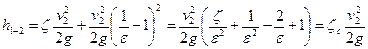, (147)
где обозначено
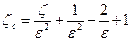. (148)
Полученное значение потерь напора подставим в уравнение (144), тогда
.
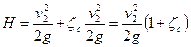Отсюда скорость истечения
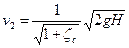. (149)
Обозначая
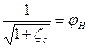, (150)
получим для скорости уравнение
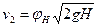. (151)
Определим расход жидкости
.
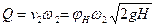Но для насадка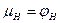 
и
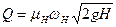, (152)
где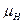 
– коэффициент расхода насадка; 
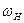– площадь живого сечения насадка.
Таким образом, уравнения для определения скорости и расхода жидкости через насадок имеют тот же вид, что и для отверстия, но другие значения коэффициентов. Для коэффициента сжатия струи (при больших значениях Re и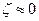 
) можно приближенно принять 
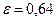, и тогда по формулам (148) и (149) получается 
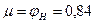. Фактически происходят и потери по длине, поэтому для истечения воды в обычных условиях можно принимать 
.
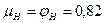Сравнивая коэффициенты расхода и скорости для насадка и отверстия в тонкой стенке, устанавливаем, что насадок увеличивает расход и уменьшает скорость истечения.
Характерной особенностью насадка является то, что давление в сжатом сечении меньше атмосферного. Это положение доказывается уравнением Бернулли, составленным для сжатого и выходного сечений.
Во внутренних цилиндрических насадках сжатие струи на входе больше, чем у внешних, и поэтому значения коэффициентов расхода и скорости меньше. Опытами найдены коэффициенты для воды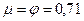 
.
В наружных конических сходящихся насадках сжатие и расширение струи на входе меньше, чем в наружных цилиндрических, но появляется внешнее сжатие на выходе из насадки. Поэтому коэффициенты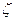 
, 
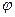и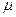 
зависят от угла конусности. С увеличением угла конусности до 13° коэффициент расхода 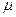растет, а с дальнейшим увеличением угла уменьшается.
Конические сходящиеся насадки применяют в тех случаях, когда нужно получить большую выходную скорость струи, дальность полета и силу удара струи (гидромониторы, пожарные стволы и т. п.).
В конических расходящихся насадках внутреннее расширение струи после сжатия больше, чем в конических сходящихся и цилиндрических, поэтому потери напора здесь возрастают и коэффициент скорости 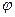уменьшается. Внешнего сжатия при выходе нет.
Коэффициенты 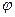и 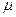зависят от угла конусности. Так, при угле конусности 
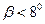значения коэффициентов можно принимать равными 
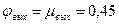; при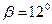 
(предельный угол) 
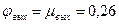. При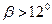 
струя вытекает, не касаясь стенок насадка, т. е. как из отверстия без насадка.
Значении коэффициентов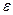 
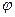, и 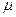для насадок
| Тип насадок | | | |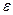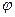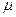
| Наружный цилиндрический…….. | 0 82 | 0,82 | |
| Внутренний цилиндрический .......... | 0,71 | 0,71 | |
Конический сходящийся при 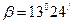 ………………………….. | 0,982 | 0,963 | 0,946 |
Конический расходящийся 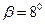 ... | 0,45 | 0,45 | |
| Коноидальный ...........................…… | 0,98 | 0,98 |
Примечание. Для конических насадок коэффициенты дапы для выходного сечения.
Конические расходящиеся насадки применяют в тех случаях, когда необходимо уменьшить скорость истечения, например, насадки для подачи смазочных масел и т. п. В конических расходящихся насадках в месте сжатия струи создается большой вакуум, поэтому их еще применяют там, где требуется создать большой эффект всасывания (эжекторы, инжекторы и т. п.).
Коноидальные насадки имеют очертания формы струи, вытекающей через отверстие в тонкой стенке. Для этих насадок значение коэффициентов составляет: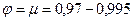 
.
Их применяют в пожарных брандспойтах, но редко, так как изготовление их очень сложное.
Для коноидально-расходящейся насадки можно получить коэффициент расхода больше единицы за счет увеличения выходного сечения.
В таблице приводятся средние значения коэффициентов для различных насадок.
НАСОСЫ
Общие сведения
Насосами называются машины, служащие для перекачки и создания напора жидкостей всех видов, механической смеси жидкостей с твердыми и коллоидными веществами и газов. Следует заметить, что машины для перекачки и создания напора газов (газообразных жидкостей) выделены в отдельные группы и получили название вентиляторов и компрессоров и служат предметом специального изучения, поэтому в данном разделе не рассматриваются.
Насосы в настоящее время являются самым распространенным видом машин.
По принципу действия насосы подразделяются на:
а) центробежные, у которых перекачка и создание напора происходят вследствие центробежных сил, возникающих при вращении рабочего колеса;
б) осевые (пропеллерные) насосы, рабочим органом у которых служит лопастное колесо пропеллерного типа. Жидкость в этих насосах перемещается вдоль оси вращения колеса;
в) поршневые и скальчатые насосы, в которых жидкость перемещается при возвратно-поступательном движении поршня или скалки. К этой группе можно отнести простейший вид поршневых насосов - диафрагмовые насосы, у которых рабочим органом служит резиновая или кожаная диафрагма, совершающая возвратно-поступательные движения;
г) тараны, работающие за счет энергии гидравлического удара;
д) струйные насосы, в которых перемещение жидкости осуществляется за счет энергии потока вспомогательной жидкости, пара или газа;
е) эрлифты (воздушные водоподъемники), в которых рабочим телом является сжатый воздух.
В зависимости от назначения и принципа действия конструктивное исполнение насосов самое различное. Ниже рассматривается устройство, принцип работы, характеристика и применение основных групп насосов.