Истечение жидкости из малого отверстия в тонкой стенке

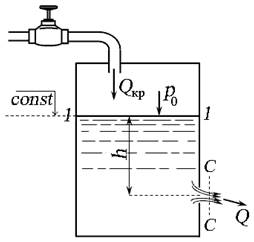
Рассмотрим истечение жидкости через отверстие диаметром d в стенке бака, расположенное на глубине h, в газовую среду. Свободная поверхность жидкости в баке находится под давлением р₀ (рис. 5.1).

а) б)

Рис. 5.1. Истечение жидкости из малого отверстия в атмосферу:

а) – схема истечения; б) – сжатие струи при истечении

Уровень жидкости в баке по плоскости 1 – 1 поддерживается постоянным (количество жидкости, вытекающей из крана Q_кр, равно количеству жидкости Q, истекающей из отверстия в боковой стенке бака), то есть истечение происходит при постоянном напоре.

Скорости истечения на верхней и нижней границах истекающей из отверстия струи можно считать равными, если истечение происходит из малого отверстия.

Малым называется отверстие, если при истечении из него распределение скоростей в живом сечении струи можно считать равномерным. При этом должно выполняться условие:

.

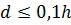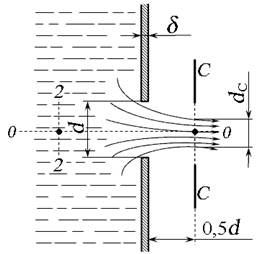
Боковая стенка не оказывает влияние на характер истечения, если толщина стенки не превышает половины диаметра отверстия (δ ≤ 0,5d). В этом случае потери напора аналогичны потерям при внезапном сужении потока, а сама стенка будет называться тонкой.

Частицы жидкости, приближаясь к отверстию, двигаются из всего близлежащего объёма по различным траекториям. Многие из них при попадании в отверстие должны изменить свою траекторию на 90º. Поскольку каждая частица имеет свою массу, то мгновенно изменить направление своего движения она не может. Следствием этого является сжатие струи жидкости при истечении (сечение С – С, рис. 5.1, б). Формирование сжатого сечения струи диаметром d_c заканчивается на расстоянии примерно 0,5d.

Для оценки степени сжатия струи используют коэффициент сжатия ε (эпсилон), равный отношению площади струи в сжатом сечении S_с к площади отверстия S. Для круглого отверстия:

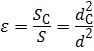, (5.1)

где S_С и d_С – площадь сжатого сечения и диаметр струи в сжатом сечении;

S и d – площадь и диаметр отверстия, через которое происходит истечение.

Для определения скорости истечения и расхода жидкости составим уравнение Бернулли для сечений 1 – 1 и С – С относительно плоскости сравнения 0 – 0, проходящей через центр сжатого сечения:

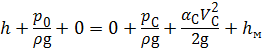, (5.2)

где р_С – давление в сжатом сечении;

α_С и V_C – коэффициент Кориолиса и средняя скорость жидкости в сжатом сечении;

h_м – местные потери напора при истечении.

Местные потери при истечении:

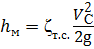, (5.3)

где ζ_т.с. – коэффициент потерь при истечении через отверстие в тонкой стенке.

С учётом (5.3) уравнение Бернулли (5.2) примет вид:

.

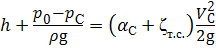Выражение в левой части уравнения является статическим напором Н_ст, под действием которого происходит истечение:

.

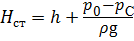Тогда средняя скорость V_С в сжатом сечении струи равна:

,

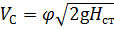где φ – коэффициент скорости, .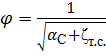

Коэффициент скорости φ отражает влияние распределения местных скоростей в сжатом сечении α_С и потерь напора ζ_т.с..

Определим расход с учётом формулы (5.1):

,

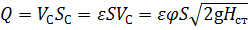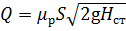, (5.4)

где μ_р – коэффициент расхода, .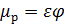

Если высоту столба жидкости h определить как 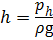, где р_h – давление, создаваемое высотой столба жидкости на глубине h, то статический напор Н_ст будет равен:

,

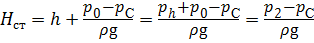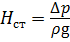, (5.5)

где ∆р – перепад давления (как правило, избыточного) до и после отверстия, под действием которого происходит истечение жидкости;

р₂ – давление в центре тяжести сечения 2 – 2.

С учётом (5.5) уравнение для определения расхода жидкости при истечении из малого отверстия в тонкой стенке при постоянном напоре примет вид:

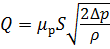. (5.6)

На рис. 5.2 показана зависимость коэффициентов расхода μ_р, скорости φ и сжатия ε от числа Рейнольдса, подсчитанного для идеальной скорости истечения, то есть истечение при отсутствии сжатия струи и сопротивления. При числах Рейнольдса Re > 10⁵ коэффициенты можно считать постоянными: ε = 0,64; φ = 0,97; μ_р = 0,62.

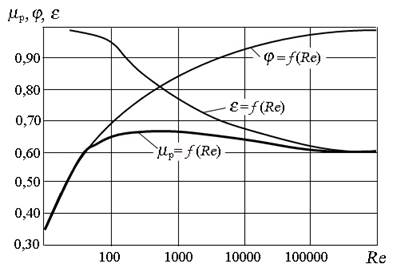
Рис. 5.2. Зависимость коэффициентов расхода μ_р, скорости φ и сжатия ε от числа Рейнольдса для круглого отверстия в тонкой стенке при полном совершенном сжатии

Согласно рис. 5.2, графики функций для определения коэффициентов μ_р, φ и ε составлены для полного совершенного сжатия.

При полном сжатии происходит сжатие струи со всех сторон. Если же с одной или нескольких сторон сжатие отсутствует, сжатие струи будет неполным. Под совершенным понимается такое полное сжатие, при котором отверстие достаточно удалено от ограничивающих поверхностей, и они не влияют на условия сжатия струи. Согласно опытным данным, это расстояние должно быть не менее 3d для круглого отверстия, или утроенного соответствующего линейного размера – для прямоугольного.

При несовершенном сжатии, а тем более при неполном, коэффициенты истечения имеют бόльшие значения.

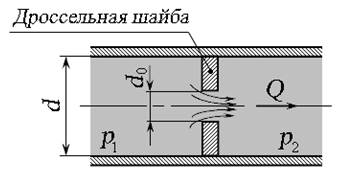
Рис. 5.3. Истечение через затопленное отверстие

Большинство гидравлической аппаратуры работает по типу отверстий в тонкой или толстой стенке, где истечение происходит через затопленное отверстие. Например, по типу отверстия в тонкой стенке происходит истечение через дроссельную шайбу (рис. 5.3). Расход при истечении в жидкость определяют по формуле (5.6), что и для истечения в газообразную среду. Истечение через отверстие диаметром d₀ происходит под действием перепада давлений :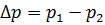

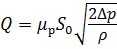, (5.7)

где S₀ – площадь отверстия, через которое происходит истечение.

Истечение через насадки

Насадком называется короткая цилиндрическая или нецилиндрическая труба длиной L_н = (3 … 5)d₀, присоединённая к отверстию (или отверстие в толстой стенке), работающая на выходе полным сечением. Различают насадки трёх типов – цилиндрические, конические и коноидальные. Рассмотрим истечение через цилиндрический насадок.

При входе в насадок струя сжимается, образуя сжатое сечение так же, как и при истечении через отверстие в тонкой стенке (сечение С – С, рис. 5.4). Затем струя постепенно расширяется до размеров отверстия, и выходит из насадка полным сечением. Такое движение жидкости в насадке называется безотрывным.

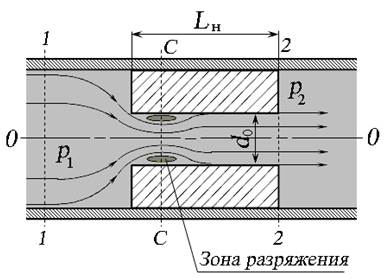
Рис. 5.4. Истечение через насадок

При истечении через насадок возникают следующие потери напора, отнесённые к скорости V₂ на выходе из насадка:

- такие же, как и при истечении через отверстие в тонкой стенке (от сечения 1 – 1 до сжатого сечения С – С)

;

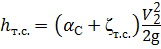- местные потери, связанные с внезапным расширением потока от сечения С – С до живого сечения, в котором поток жидкости будет сформирован

;

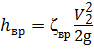- потери напора по длине L_н насадка диаметром d₀

.

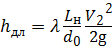Общие потери напора при истечении через насадок будут равны:

.

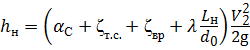Составив уравнение Бернулли для сечений 1 – 1 и 2 – 2, получим ту же формулу для определения скорости истечения на выходе из насадка, что и для истечения через отверстие в тонкой стенке:

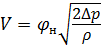, (5.8)

.

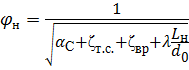где V₂ = V – средняя скорость жидкости на выходе из насадка;

φ_н – коэффициент скорости для истечения через насадок.

Расход жидкости при истечении через насадок определяют по той же формуле, что и для истечения через отверстия в тонкой стенке, но со своими коэффициентами скорости и расхода:

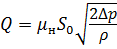, (5.9)

где μ_н – коэффициент расхода при истечении через насадок, μ_н = ε_нφ_н;

ε_н – коэффициент сжатия струи, равный отношению площади S_стр струи в живом сечении на выходе из насадка к площади S_вых самого выходного отверстия насадка, ε_н = ;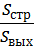

φ_н – коэффициент скорости при истечении через насадок.

Коэффициенты μ_н и φ_н определены по результатам экспериментальных исследований.

В сжатом сечении возникает кольцевая зона разряжения, за счёт которых происходит подсос жидкости при истечении через насадок. В результате этого скорость жидкости при истечении через насадок больше, чем при истечении через отверстие в тонкой стенке.

Недостаток давления (р_ат – р_вак) в зоне разряжения (в сжатом сечении) не должен быть меньше давления р_нп насыщенного пара. В противном случае происходит нарушение сплошности потока жидкости, что приводит к нарушению нормальной работы насадка. Определим р_вак, составив уравнение Бернулли для сечений С – С и 2 – 2 относительно плоскости сравнения 0 – 0, совпадающей с осью насадка:

.

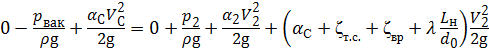Учитывая, что α_С = α₂ ≈ 1, V_C = εV₂, потери по длине примерно равны нулю, получим:

,

.

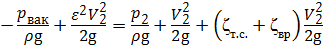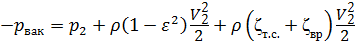По формуле (5.8) 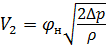, 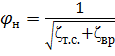. Тогда

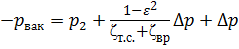. (5.10)

Коэффициент ζ_вр при внезапном расширении, отнесённый к скорости V₂, равен ζ_вр = 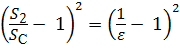. Учитывая, что 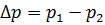, выражение (5.10) примет вид:

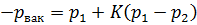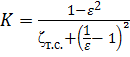, где . (5.11)

Для маловязких жидкостей (вода, бензин, керосин и т. д.) при значительных числах Рейнольдса (Re ≥ 10⁵), при полном и совершенном сжатии коэффициент K ≈ 1. Тогда значение вакуумметрического давления р_вак в сжатом сечении С – С:

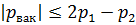, или .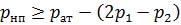

В случае, если 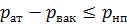, насадок работает неполным сечением по типу истечения через отверстие в тонкой стенке.

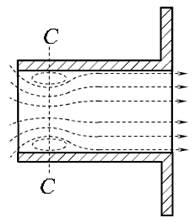
Цилиндрический насадок (рис. 5.5) может быть внешним или внутренним. Расход через внешний цилиндрический насадок будет несколько больше, чем через внутренний, так как коэффициент расхода для внешнего насадка μ_внеш = 0,82, для внутреннего μ_внутр = 0,71.

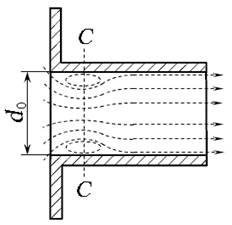
а) б)

Рис. 5.5. Цилиндрический насадок:

а) - внешний; б) - внутренний

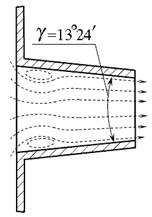
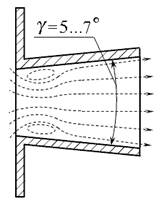
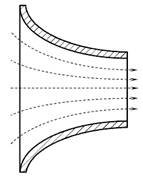
Нецилиндрические насадки могут быть конически сходящиеся, конически расходящиеся и коноидальные (рис. 5.6).

а) б) в)

Рис. 5.6. Нецилиндрические насадки:

а) - конически сходящиеся; б) - конически расходящиеся;

в) - коноидальные

Конически сходящиеся насадки имеют конусность γ = 13º24′, так как при таком значении конусности достигается максимальное значение коэффициента расхода μ_к.с. = 0,94. При таком угле конусности площадь сжатого сечения примерно равна площади выходного отверстия насадка. Выходящая из конического насадка струя характеризуется большой кинетической энергией, в связи с чем эти насадки применяют в соплах турбин, гидромониторах и пожарных брандспойтах.

Конически расходящиеся насадки характеризуются бόльшим значением вакуума в сжатом сечении, чем в цилиндрическом. Такие насадки применяют, если необходимо пропустить относительно большой расход жидкости при малых скоростях на выходе.

Коноидальные насадки имеют сложную форму, за счёт которой на входе в насадок отсутствует вакуумметрическое давление, и такие насадки работают полным сечением при любом перепаде давлений. Коноидальный насадок обеспечивает наибольшую скорость в выходном сечении, следовательно, максимальную кинетическую энергию.

В табл. 3 приведены значения коэффициентов ε_н, φ_н и μ_н для различных типов насадок.

Таблица 3

Значения коэффициентов истечения через насадки

при совершенном сжатии

Тип насадка	εн	φн	μн
Внешний цилиндрический		0,82	0,82
Внутренний цилиндрический		0,707	0,707
Конически расходящийся (γ = 5 … 7º)		0,45 … 0,5	0,45 …0,5 (по Sвых) 1 … 1,05 (по Sвх)
Конически сходящийся (γ = 13º24′)	0,98	0,96	0,94
Коноидальные		0,98	0,98