Вычисление определенного интеграла
Формула Ньютона-Лейбница.
Для вычисления определенного интеграла используется формула Ньютона-Лейбница:
Если функция 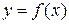 непрерывна на отрезке [a;b] и
непрерывна на отрезке [a;b] и 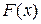 - какая-либо ее первообразная на [a;b], то имеет место формула
- какая-либо ее первообразная на [a;b], то имеет место формула
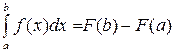 .
.
Пример. Вычислить 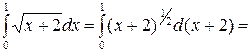
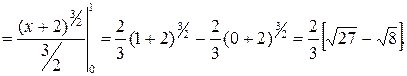
Интегрирование методом замены переменной.
Если для вычисления интеграла 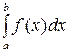 от непрерывной функции делается подстановка
от непрерывной функции делается подстановка 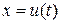 , которая удовлетворяет следующим условия:
, которая удовлетворяет следующим условия:
а) функция 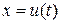 и ее производная
и ее производная 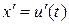 - непрерывны при
- непрерывны при 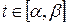
б) множеством значений функции 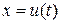 при
при 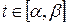 является отрезок [a,b];
является отрезок [a,b];
в) 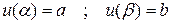 , то имеет место формула
, то имеет место формула
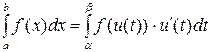 .
.
Заметим, что
1) при вычислении определенного интеграла методом замены переменной возврат к старой переменной необязателен, но при этом необходимо поменять пределы интегрирования на новые;
2) иногда удобно вместо подстановки 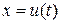 применить подстановку
применить подстановку 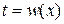 , как , например, в случае универсальной тригонометрической подстановки.
, как , например, в случае универсальной тригонометрической подстановки.
Примеры. 1. 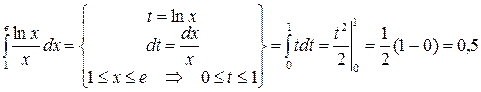
2. 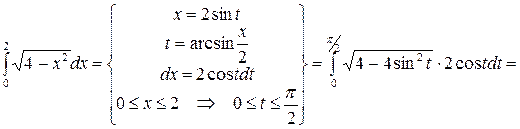
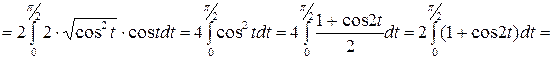
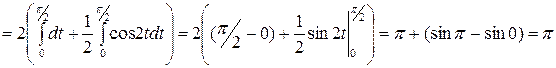
Интегрирование по частям.
Если функции 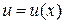 и
и 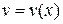 имеют непрерывные производные на отрезке [a,b], то имеет место формула
имеют непрерывные производные на отрезке [a,b], то имеет место формула
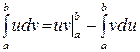 .
.
Примеры. 1. 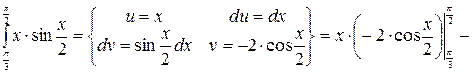
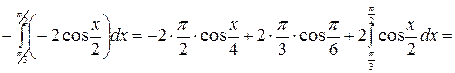
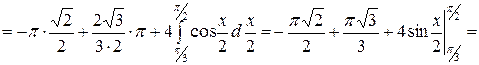
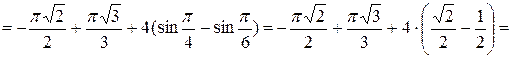
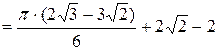 .
.
2. 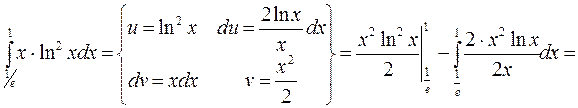
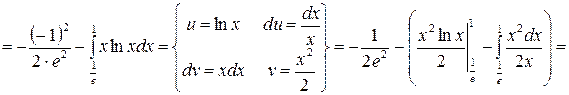
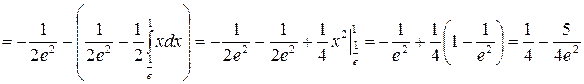 .
.
ЗАДАЧИ
1.1 а) 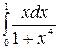 б)
б) 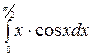 в)
в) 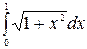
1.2 а) 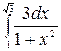 б)
б) 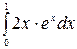 в)
в) 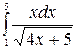
1.3 а) 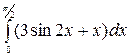 б)
б) 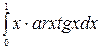 в)
в) 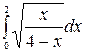
1.4 а) 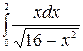 б)
б) 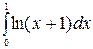 в)
в) 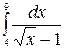
1.5 а) 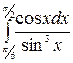 б)
б) 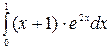 в)
в) 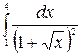
1.6 а) 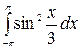 б)
б) 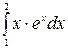 в)
в) 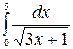
1.7 а) 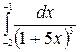 б)
б) 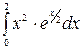 в)
в) 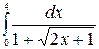
1.8 а) 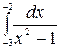 б)
б) 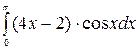 в)
в) 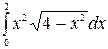
1.9 а) 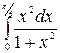 б)
б) 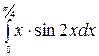 в)
в) 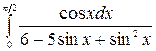
1.10 а) 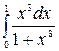 б)
б) 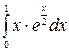 в)
в) 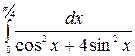
1.11 а) 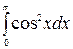 б)
б) 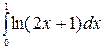 в)
в) 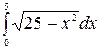
1.12 а) 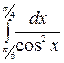 б)
б) 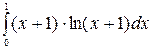 в)
в) 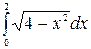
1.13 а) 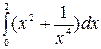 б)
б) 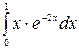 в)
в) 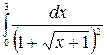
1.14 а) 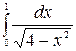 б)
б) 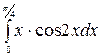 в)
в) 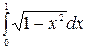
1.15 а) 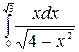 б)
б) 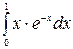 в)
в) 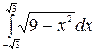
1.16 а) 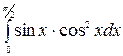 б)
б) 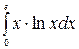 в)
в) 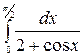
1.17 а) 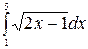 б)
б) 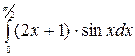 в)
в) 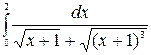
1.18 а) 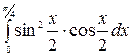 б)
б) 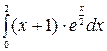 в)
в) 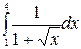
1.19 а) 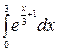 б)
б) 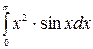 в)
в) 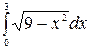
1.20 а) 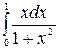 б)
б) 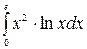 в)
в) 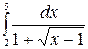
Геометрический и физический смысл
Определенного интеграла.
1) Пусть на отрезке [a,b] задана непрерывная неотрицательная функция 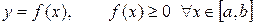 . Рассмотрим фигуру, образованную параллельными прямыми
. Рассмотрим фигуру, образованную параллельными прямыми 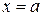 и
и 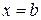 , осью OX и графиком кривой
, осью OX и графиком кривой 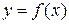 . Такая фигура называется криволинейной трапецией.
. Такая фигура называется криволинейной трапецией.
Площадь криволинейной трапеции, ограниченной прямыми 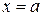 и
и 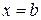 , осью OX и графиком неотрицательной функции
, осью OX и графиком неотрицательной функции 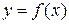 , численно равна определенному интегралу от этой функции.
, численно равна определенному интегралу от этой функции.
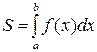
2) Пусть материальная точка М перемещается под действием силы 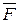 , направленной вдоль оси ОХ , причем величина этой силы описывается функцией
, направленной вдоль оси ОХ , причем величина этой силы описывается функцией 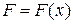 , где x – абсцисса точки М.
, где x – абсцисса точки М.
Тогда работа A переменной силы 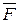 по перемещению материальной точки М вдоль оси ОХ из точки
по перемещению материальной точки М вдоль оси ОХ из точки 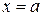 в точку
в точку 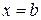 равна определенному интегралу от величины этой силы, взятому по отрезку [a,b].
равна определенному интегралу от величины этой силы, взятому по отрезку [a,b].
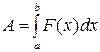 .
.
Кроме указанной задачи в физике с помощью определенных интегралов решают задачи о массе М стержня с переменной плотностью 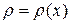 , имеющей начало
, имеющей начало 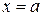 и конец
и конец 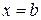 , и о пути S, пройденном материальной точкой за промежуток времени
, и о пути S, пройденном материальной точкой за промежуток времени 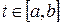 со скоростью
со скоростью 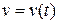 , т.е.
, т.е.
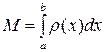
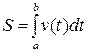 .
.
Пример 1. Скорость тела задается формулой 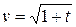
 . Найти путь, пройденный телом за первые 8 с. после начала движения.
. Найти путь, пройденный телом за первые 8 с. после начала движения.
Опираясь на физический смысл определенного интеграла, имеем
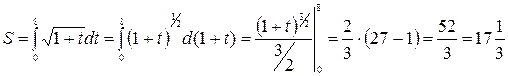 .
.
Пример 2. Найти работу, затрачиваемую на растяжение пружины на 10 см, если известно, что сила 100Н растягивает пружину на 0,01 м?
Для решения задачи воспользуемся законом Гука, согласно которому 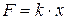 , где k – коэффициент пропорциональности. Найдем этот коэффициент, используя условия задачи. Так как 100Н=
, где k – коэффициент пропорциональности. Найдем этот коэффициент, используя условия задачи. Так как 100Н= 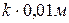 , то
, то 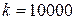 , следовательно, переменная сила будет описываться формулой
, следовательно, переменная сила будет описываться формулой 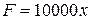 . Далее, необходимо все начальные данные перевести в единую систему измерения, например в метры, тогда требование задачи сводится к тому, что пружину необходимо растянуть на 0,1 м. Используя формулу для вычисления работы, получим
. Далее, необходимо все начальные данные перевести в единую систему измерения, например в метры, тогда требование задачи сводится к тому, что пружину необходимо растянуть на 0,1 м. Используя формулу для вычисления работы, получим
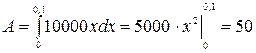 Дж.
Дж.
