Вычисление определенного интеграла

Определенный интеграл вычисляется по формуле Ньютона-Лейбница

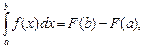
где F(x) ‒ первообразная для функции f(x). Таким образом, определенный интеграл равен разности значений первообразной на концах промежутка.

Сформулируем и докажем теоремы, обосновывающие справедливость этой основной формулы математического анализа.

Теорема о существовании первообразной. Если функция f(x) непрерывна на отрезке [a, b], то функция 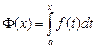дифференцируема в любой внутренней точке х этого отрезка, причем Ф'(х) = f(x), то есть функция Ф(х) является первообразной функции f(x).

Доказательство. Найдем производную функции Ф(x), являющейся интегралом с переменным верхним пределом. Для этого вначале выберем 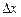столь малым, чтобы точка х + ∆x лежала внутри отрезка [а, b], и построим приращение функции Ф(x).

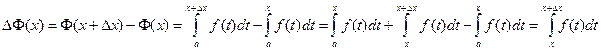
К полученному интегралу применим теорему о среднем:

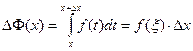, где

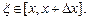
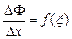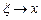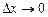Следовательно, . Поскольку f(x) непрерывна и при , то 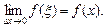Поэтому производная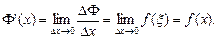

Этим показано, что функция, являющаяся интегралом от функции f(x) с постоянным нижним и переменным верхним пределом х, есть одна из первообразных функций от функции f(x). Этот факт, установленный Ньютоном и Лейбницем, показывает, что дифференциальное и интегральное исчисление представляет собой нечто единое, и известен как основная теорема математического анализа.

Теперь выведем основную формулу математического анализа.

Теорема. Если функция f(x) непрерывна на отрезке [а, b], то

.

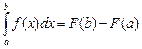Доказательство. В силу непрерывности на отрезке [a, b] функция f(x) интегрируема и на основании основной теоремы математического анализа имеет первообразную .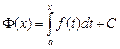

Первообразных у функции бесконечно много, и все они отличаются друг от друга на произвольную постоянную (обозначим ее через С). Поэтому, если F(x) — первообразная для f(х), то:

,

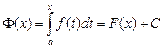Константу легко выразить через значение первообразной F в точке а. Действительно принимая во внимание, что 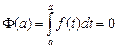, получим: -F(a) = С. Поскольку 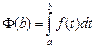, то для точки b с переменной интегрирования х, получаем основную формулу математического анализа — формулу Ньютона-Лейбница.

Эта формула дает следующее правило: для вычисления определенного интеграла необходимо найти первообразную подынтегральной функции, а затем вычислить разность значений первообразной на верхнем и нижнем пределе.

Пример. Вычислить интеграл .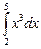

Решение. Одна из первообразной функции х³ есть функция х⁴/4. Поэтому:

.

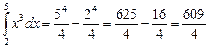Формулу Ньютона-Лейбница при вычислении определенного интеграла удобно записывать, используя знак подстановки в следующем виде: .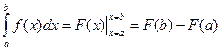

При вычислении определенного интеграла используются те же основные приемы, что и при вычислении неопределенного интеграла.

1.Формула интегрирования по частям.

.

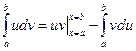Пример. Вычислить .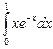

Решение. Прямому вычислению данного интеграла препятствует наличие сомножителя х в подынтегральном выражении поскольку производная от х по х равна 1, то целесообразно положить u = х. Тогда:

.

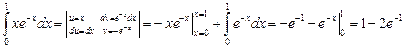2.Замена переменной в определенном интеграле.

Во многих случаях подынтегральное выражение можно упростить, если заметить, что его часть является дифференциалом некоторой функции. Тогда можно записать:

,

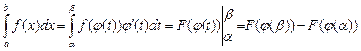где x = j(t), j(α) = a, j(β) = b, т. е. [j(α); j(β)] = [a, b].

Несобственные интегралы

Для существования определенного интеграла необходимо, чтобы промежуток интегрирования был конечен и непрерывная подынтегральная функция ограничена. Когда не выполняется одно или оба эти условия, приходится прибегать к понятию несобственного интеграла.