Вычисление определенного интеграла методом подстановки.
Вычисление определенного интеграла методом подстановки состоит в следующем:
1) часть подынтегральной функции заменить новой переменной;
2) найти новые пределы определенного интеграла;
3) найти дифференциал от обеих частей замены;
4) все подынтегральное выражение выразить через новую переменную (после чего должен получиться табличный интеграл);
5) вычислить полученный определенный интеграл.
Пример 18.Вычислить интеграл 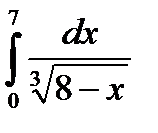 .
.
Решение. Введем подстановку 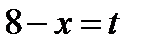 , тогда
, тогда 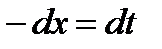 ,
, 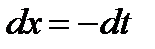 . Определим пределы интегрирования для переменной t. При x=0 получаем
. Определим пределы интегрирования для переменной t. При x=0 получаем 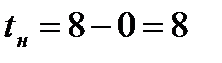 , при x=7 получаем
, при x=7 получаем 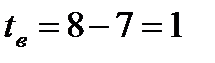 .
.
Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим
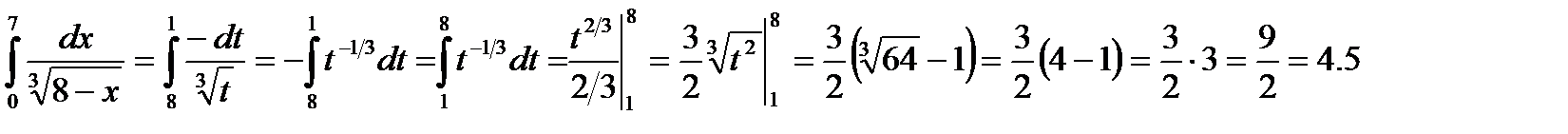 .
.
Пример 19.Вычислить интеграл 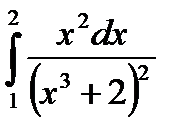 .
.
Решение. Произведем подстановку 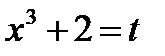 , тогда
, тогда 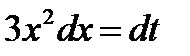 ,
, 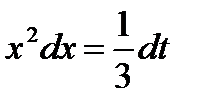 . Определим пределы интегрирования для переменной t. При x=1 получаем
. Определим пределы интегрирования для переменной t. При x=1 получаем 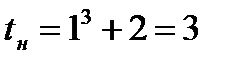 , при x=2 получаем
, при x=2 получаем 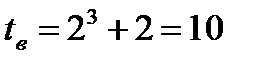 .
.
Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим
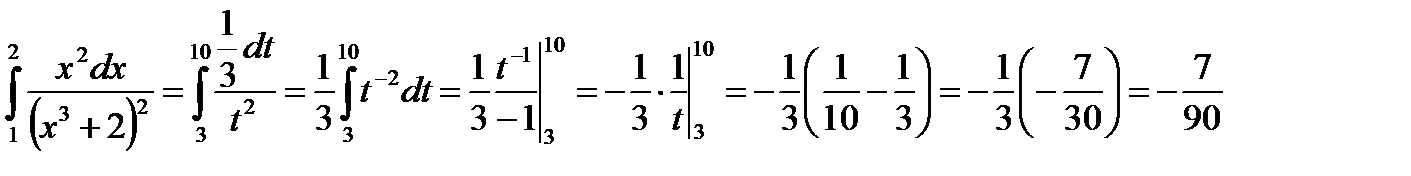 .
.
Пример 20.Вычислить интеграл 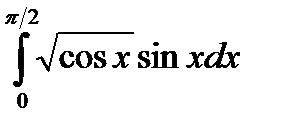 .
.
Решение. Положим 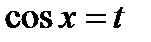 , тогда
, тогда 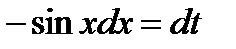 и
и 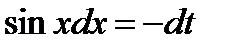 . Определим пределы интегрирования для переменной t:
. Определим пределы интегрирования для переменной t: 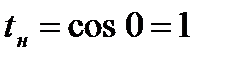 ,
, 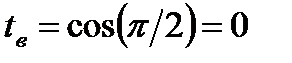 .
.
Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим
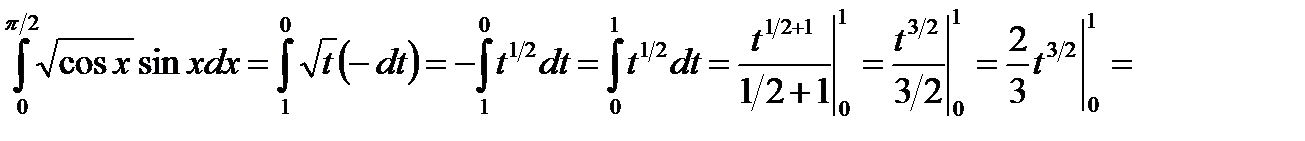
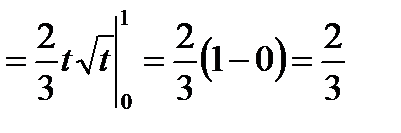
Пример 21.Вычислить интеграл 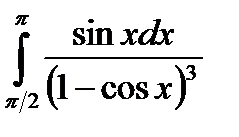 .
.
Решение. Пусть 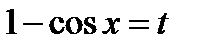 ,
, 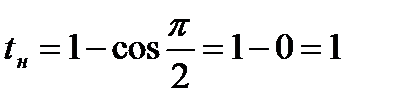 ,
, 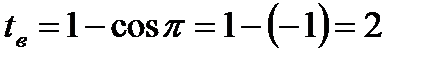 ,
, 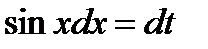 .
.
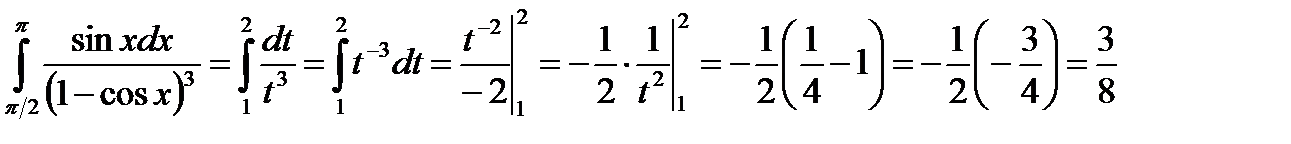
Пример 22.Вычислить интеграл 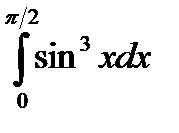 .
.
Решение. Сначала преобразуем подынтегральное выражение:
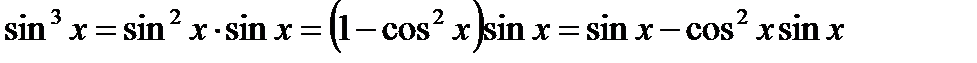 .
.
Затем вычислим интеграл от разности функций, заменив его разностью определенных интегралов от каждой функции:
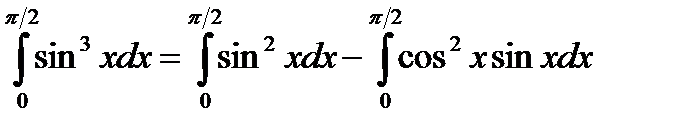 .
.
Вычислим каждый интеграл отдельно:
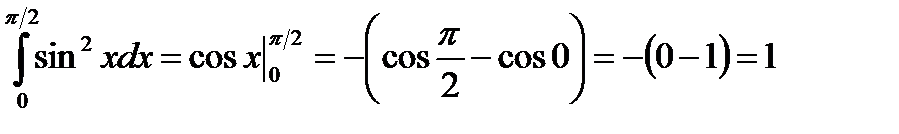 ;
;
Пусть 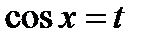 ,
, 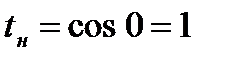 ,
, 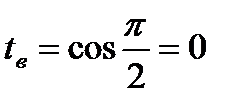 ,
, 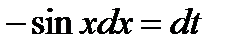 ,
, 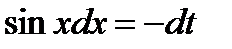 .
.
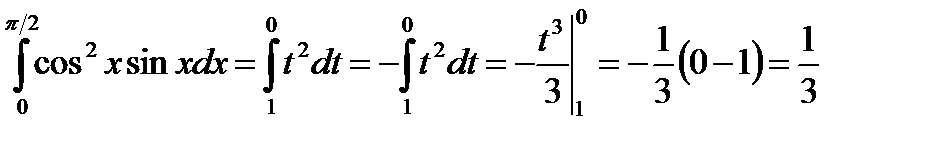 .
.
Тогда
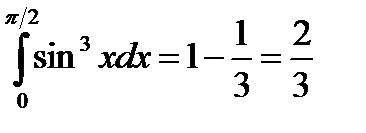
Интегрирование по частям.
Здесь используют формулу: 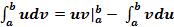
Пример 23.Вычислите интеграл: 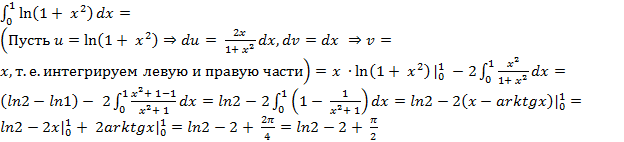
Пример 24.Вычислите интеграл: 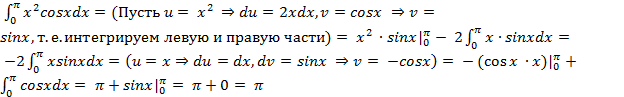
Приложение определенного интеграла.
Понятие определенного интеграла широко применяется для вычисления различных геометрических и физических величин.
Площади плоских фигур.
1. Фигура ограниченная графиком непрерывной и неотрицательной на отрезке [a;b] функции f(x), осью Ох и прямыми х = а, х = b. Площадь данной фигуры находится по S = 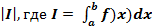 (1)
(1)
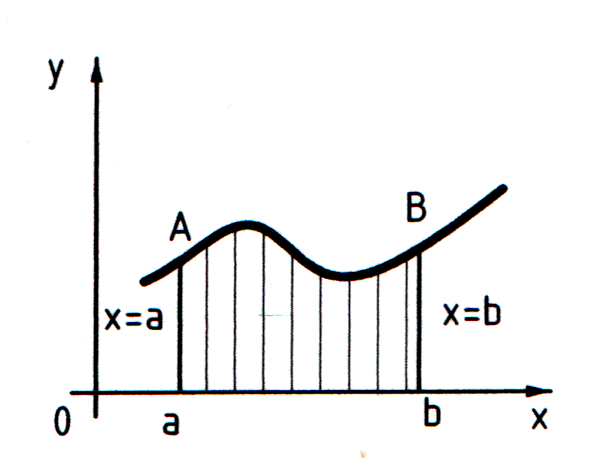
Пример 25: Вычислить площадь фигуры ограниченной линиями 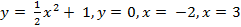 . Решение: Построим графики данных функций: а)
. Решение: Построим графики данных функций: а) 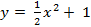 - кв. ф., график – парабола, ветви направленны вверх. Вершина находится в точке с координатами (0; 1).
- кв. ф., график – парабола, ветви направленны вверх. Вершина находится в точке с координатами (0; 1).
Находим доп. точки, для этого строим таблицу:
| Х | ±1 | ±2 | ±3 |
| у | 1,5 | 5,5 |
б) у = 0 – ось Ох
в) х = - 2, х = 3 – прямые, У у = 
параллельные оси Оу
Х = - 2 1 х = 3
0 Х
- 2 1 3
S = 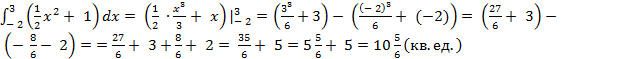
Пример 26: Вычислить площадь фигуры ограниченной линиями y = - x2 – 1, y = 0, x = - 1, x = 2.
Решение: Построим графики данных функций: а) у = - х2 – 1 – квадратичная функция, графиком является парабола, ветви направлены вниз. Вершина находится в точке с координатами (0; - 1). Находим доп. точки, для этого строим таблицу:
| Х | ±1 | ± 2 | ± 3 |
| У | - 2 | - 5 | - 10 |
б) у = 0 – ось Ох; х = - 1, х = 2 – прямые параллельные оси Оу
У
0 Х
- 2 - 1 1 2 3
Х = -1 Х = 2
У = - х2 – 1
I = 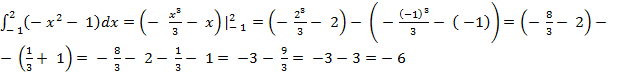
S = 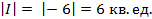
2. Фигура, ограниченная графиками двух непрерывных на отрезке [a; b] функций f(x) и g(x) и прямыми x = a, x = b, где f(x) ≥ g(x). В этом случае искомая площадь вычисляется по формуле
S = 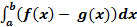 (2)
(2)
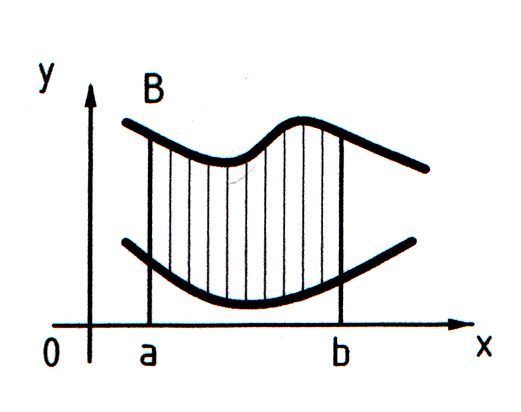
Пример 27. Вычислить площадь фигуры ограниченной линиями 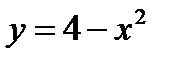 ,
, 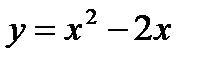 .
.
Решение:1) Найдем пределы интегрирования, т.е. абсциссы точек пересечения графиков функций 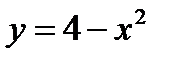 и
и 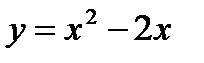 . Для этого решим систему
. Для этого решим систему
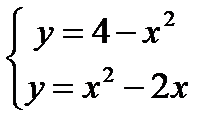
Имеем 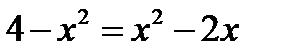
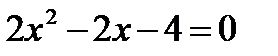 ,
, 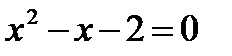 , a = 1, b= - 1, c = - 2
, a = 1, b= - 1, c = - 2
D = 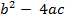
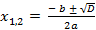
D = (- 1)2 - 4· 1· ( - 2) =9 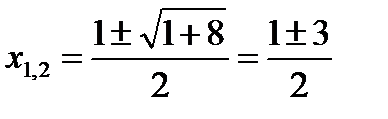 ,
, 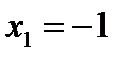 ,
, 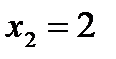 .
.
Следовательно a = - 1, b = 2
2)Построим графики функций:
а) y = 4 – x2 - квадратичная функция, график – парабола, ветви вниз. Вершина находится в точке с координатами (0;4). Находим доп. точки, для этого строим таблицу:
| Х | ±1 | ± 2 | ± 3 |
| У | - 5 |
б) y = x2 - 2x – квадратичная функция, график – парабола, ветви направлены вверх. Найдем координаты вершины параболы: хв = - 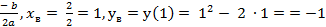 .
.
Вершина находится в точке с координатами (1; - 1). Находим доп. точки, для этого строим таблицу:
У
| Х | - 1 | ||
| У |
у = х2 – 2х
0 Х
У = 4 – х2
Искомую площадь вычисляем по формуле (2):
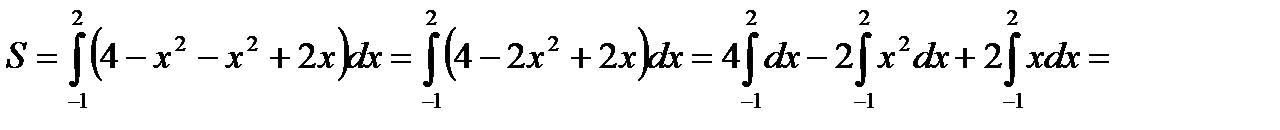
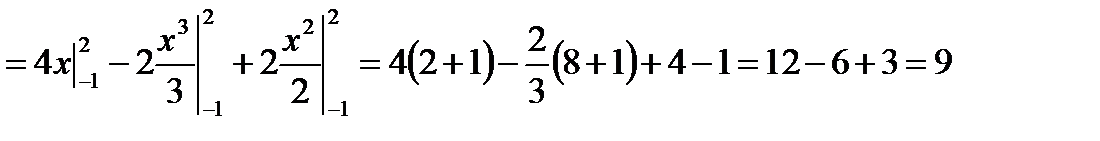 ;
; 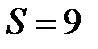 кв. ед.
кв. ед.
3.Фигура, ограничена осью Ох, прямыми x = a, x = b и графиком функции f(x), которая непрерывна на данном отрезке и меняет свой знак конечное число раз на этом отрезке. В этом случае отрезок [a;b] разбивают на части. Искомая площадь Sчисленно равна алгебраической сумме интегралов, взятых по каждому из полученных отрезков, т. е.
S = S1 + S2, S1 = 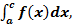 S2 =
S2 = 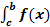 dx
dx
У
S1
a c b X
S2
Пример 28: Вычислите площадь фигуры, ограниченной линиями y = sinx, x = -  , x=
, x= 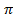 . Решение: Построим графики функций: У
. Решение: Построим графики функций: У
х = -  0 π Х
0 π Х
S = S1 + S2; S1 = 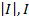 =
= 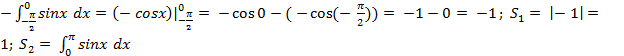 = (- cos x)
= (- cos x) 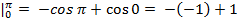 =2; S = 1 + 2 = 3 кв. ед.
=2; S = 1 + 2 = 3 кв. ед.
4.Фигура ограничена графиками трех и более непрерывных на отрезка [a;b] функций. В этом случае искомую площадь вычисляют как алгебраическую сумму площадей, вычисление каждой из которых сводится к одному из предыдущих случаев.
Пример 29: Вычислите площадь фигуры, ограниченной линиями y = 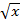 ; y =
; y =  ; y = 2x. Решение: 1) Находим пределы интегрирования, т.е. точки пересечения графиков функций. Для этого необходимо решить 3 системы уравнений:
; y = 2x. Решение: 1) Находим пределы интегрирования, т.е. точки пересечения графиков функций. Для этого необходимо решить 3 системы уравнений:
а) 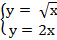
Имеем 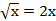 , возведем обе части уравнения в квадрат
, возведем обе части уравнения в квадрат
х = 4х2
4х2 – х = 0
х(4х – 1) = 0
х1 = 0 или 4х – 1 = 0
4х = 1
х2 = 
б) 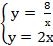 Имеем
Имеем 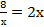
8 = 2х2
х2 = 4
х1,2 = ± 2
в) 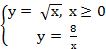 Имеем
Имеем 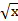 =
= 
х = 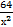
х3 = 64
х = 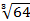 = 4
= 4
2) Построим графики данных функций:
а) у = 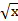 - графиком является ветвь параболы, расположенная в 1 четверти , т. к. х ≥ 0.
- графиком является ветвь параболы, расположенная в 1 четверти , т. к. х ≥ 0.
| Х | ||||
| у |
б) y = 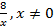 - обратная пропорциональность, графиком является гипербола, расположенная в I и в III координатных четвертях.
- обратная пропорциональность, графиком является гипербола, расположенная в I и в III координатных четвертях.
| Х | ± 1 | ± 2 | ± 4 | ± 8 |
| У | ± 8 | ± 4 | ± 2 | ± 1 |
в) у = 2х – прямая пропорциональность, графиком является прямая, проходящая через начала координат.
| Х | ||
| У |
Т. К. х ≥ 0, то графики достаточно построить в 1 координатной четверти
У у = 
у = 2х
У = 
1 2
3) Находим площадь фигуры. Она равна сумме площадей на отрезке [ 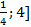 , т. е.
, т. е.
S = S1 + S2, где S1 = 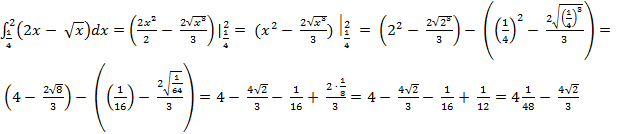 (кв. ед.)
(кв. ед.)
S2 = 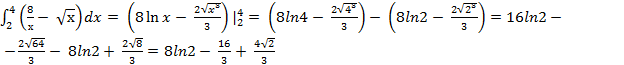
S = 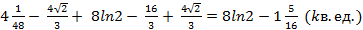
Дифференциальные уравнения.
Понятие о дифференциальном уравнении. Дифференциальным уравнением называется уравнение, связывающее независимую переменную, искомую функцию, ее производную (или дифференциал аргумента и дифференциал функции).
Если дифференциальное уравнение содержит производную или дифференциал не выше первого порядка, то оно называется дифференциальным уравнением первого порядка. Общий вид такого уравнения 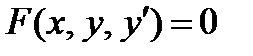 , где
, где 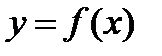 - искомая функция,
- искомая функция, 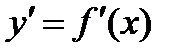 - ее производная по x, а F – заданная функция переменных x, y, y’.
- ее производная по x, а F – заданная функция переменных x, y, y’.
Общим решением дифференциального уравнения первого порядка называется функция 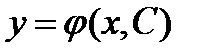 от x и произвольной постоянной C, обращающая это уравнение в тождество по x.
от x и произвольной постоянной C, обращающая это уравнение в тождество по x.
Общее решение, записанное в неявном виде 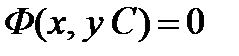 , называется общим интегралом.
, называется общим интегралом.
Частным решением уравнения 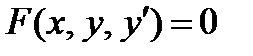 называется решение, полученное из общего решения при фиксированном значении C:
называется решение, полученное из общего решения при фиксированном значении C: 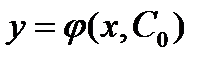 , где
, где 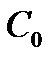 - фиксированное число.
- фиксированное число.
Частным интегралом уравнения 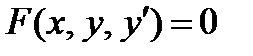 называется интеграл, полученный из общего интеграла при фиксированном значении C:
называется интеграл, полученный из общего интеграла при фиксированном значении C: 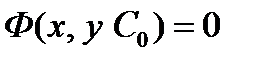 .
.
График любого частного решения дифференциального уравнения 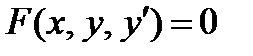 называется дифференциальной кривой. Общему решению (и общему интегралу) этого уравнения соответствует семейство интегральных кривых, зависящих от одного параметра.
называется дифференциальной кривой. Общему решению (и общему интегралу) этого уравнения соответствует семейство интегральных кривых, зависящих от одного параметра.
Задача нахождения частного интеграла дифференциального уравнения n-го порядка (n=1, 2, 3, …), удовлетворяющего начальным условиям вида 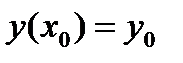 ,
, 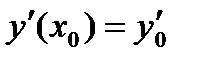 ,
, 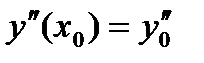 , …,
, …, 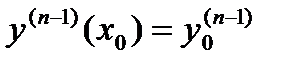 , называется задачей Коши.
, называется задачей Коши.
Задача Коши для дифференциального уравнения первого порядка состоит в том, чтобы найти решение, удовлетворяющее начальному условию 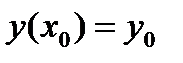 . Другими словами, из всех интегральных кривых данного дифференциального уравнения требуется выделить ту, которая проходит через точку
. Другими словами, из всех интегральных кривых данного дифференциального уравнения требуется выделить ту, которая проходит через точку 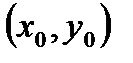 .
.
Пример 1. Составить уравнение кривой 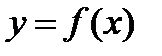 , если угловой коэффициент касательной, проведенной в любой точке кривой равен 2x.
, если угловой коэффициент касательной, проведенной в любой точке кривой равен 2x.
Решение. Так как на основании геометрического смысла производной 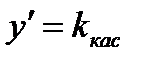 , то получим дифференциальное уравнение первого порядка:
, то получим дифференциальное уравнение первого порядка:
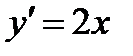 ,
, 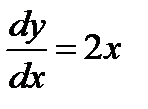 ,
, 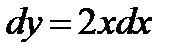 .
.
Чтобы найти искомую функцию 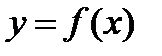 , надо проинтегрировать обе части уравнения
, надо проинтегрировать обе части уравнения 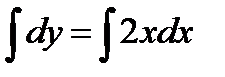 . Отсюда получим общее решение дифференциального уравнения:
. Отсюда получим общее решение дифференциального уравнения: 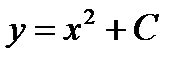 . Геометрически это решение представляет собой семейство парабол с вершиной на оси Oy, симметричных относительно этой оси (рис. 18).
. Геометрически это решение представляет собой семейство парабол с вершиной на оси Oy, симметричных относительно этой оси (рис. 18).
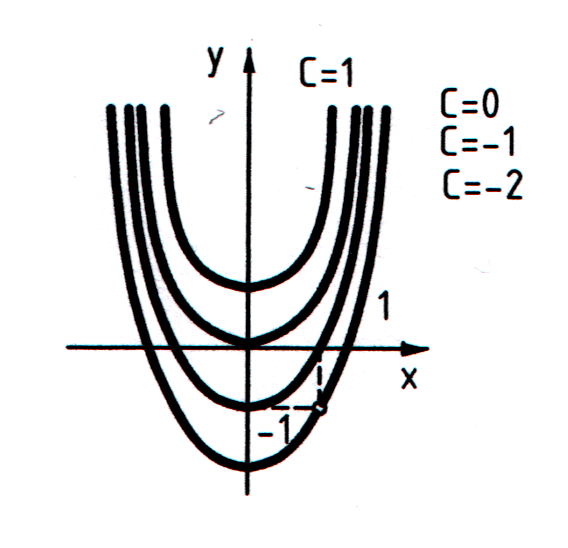
Рисунок 18.
Чтобы из общего решения выделить частное решение, надо задать начальные условия. Пусть 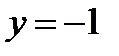 при
при 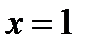 , тогда общее решение примет вид
, тогда общее решение примет вид 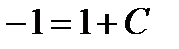 , откуда
, откуда 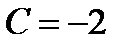 . Геометрически частное решение
. Геометрически частное решение 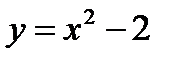 представляет собой параболу, проходящую через точку (1, -1) (рис. 68).
представляет собой параболу, проходящую через точку (1, -1) (рис. 68).
Дифференциальные уравнения с разделяющимися переменными. Общий вид такого уравнения
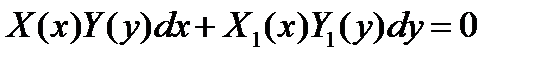
где 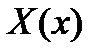 ,
, 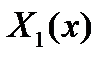 - функции только от x,
- функции только от x, 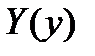 ,
, 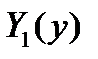 - функции только от y.
- функции только от y.
Поделив обе части уравнения на произведение 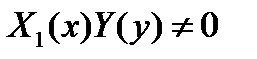 , получим уравнение с разделяющимися переменными:
, получим уравнение с разделяющимися переменными: 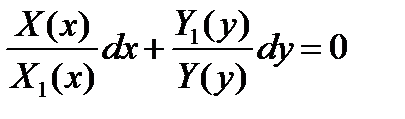 .
.
Общий интеграл этого уравнения имеет вид
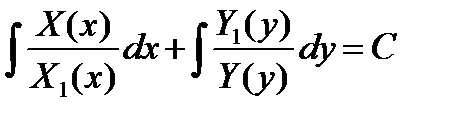 .
.
Замечание. Если произведение 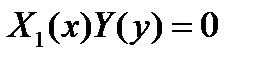 при x=a и y=b, то эти функции x=a и y=b являются решениями дифференциального уравнения при условии, что при этих значениях x и y уравнение не теряет числового смысла. Геометрически эти решения представляют собой прямые, параллельные осям координат.
при x=a и y=b, то эти функции x=a и y=b являются решениями дифференциального уравнения при условии, что при этих значениях x и y уравнение не теряет числового смысла. Геометрически эти решения представляют собой прямые, параллельные осям координат.
Пример 2. Решить уравнение 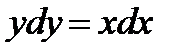 . Найти частное решение, удовлетворяющее условию y=4 при x=-2.
. Найти частное решение, удовлетворяющее условию y=4 при x=-2.
Решение. Это уравнение с разделенными переменными. Интегрируя, находим общее решение уравнения: 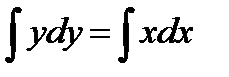 ,
, 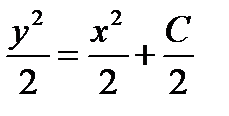 .
.
Для получения более простого по форме общего решения постоянное слагаемое в правой части представлено в виде C/2. Тогда
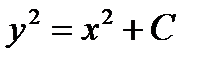 .
.
Подставив в общее решение значения y=4 и x=-2, получим 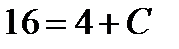 , откуда
, откуда 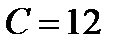 .
.
Пример 3. Найти общий интеграл дифференциального уравнения 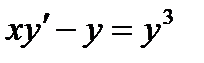
Решение. Так как 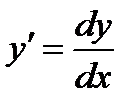 , то
, то 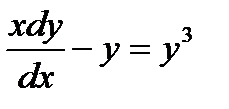 , откуда
, откуда 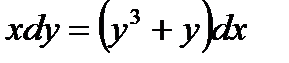 .
.
Разделим обе части уравнения на произведение 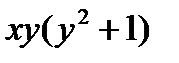 :
: 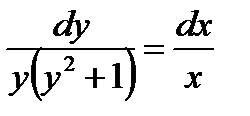 .
.
Преобразуем дробь: 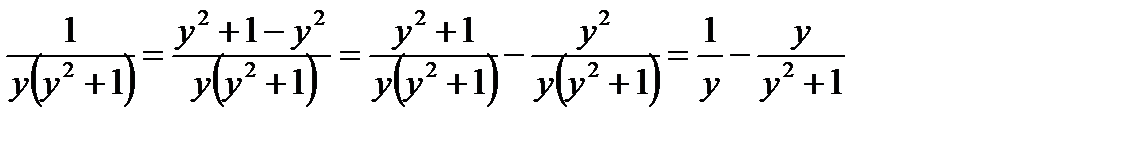 .
.
Тогда 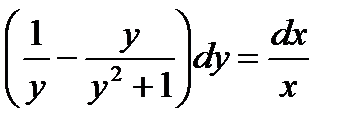 .
.
Интегрируя, находим
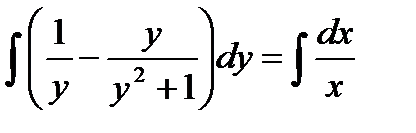 ,
, 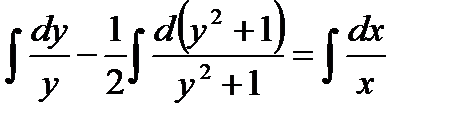 ,
, 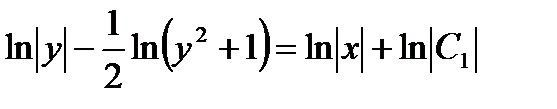 .
.
Для облегчения потенцирования и получения более простого по форме общего решения постоянное слагаемое в правой части представлено в виде 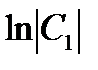 . После потенцирования получим
. После потенцирования получим
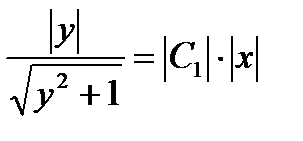 , откуда
, откуда 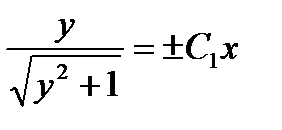 , или
, или 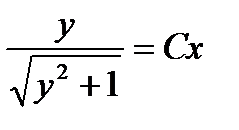 , где
, где 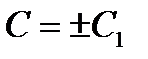 .
.
Произведение 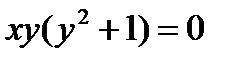 при
при 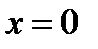 и
и 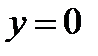 . При этих значениях x и y дифференциальное уравнение не теряет числового смысла, поэтому
. При этих значениях x и y дифференциальное уравнение не теряет числового смысла, поэтому 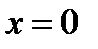 и
и 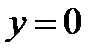 - решение уравнения, но решение
- решение уравнения, но решение 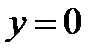 входит в решение
входит в решение 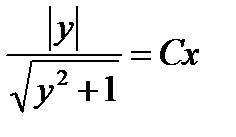 при
при 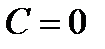 .
.
Значит, решения уравнения имеют вид 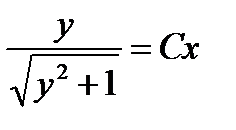 и
и 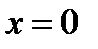 .
.
Пример 4. Решить уравнение 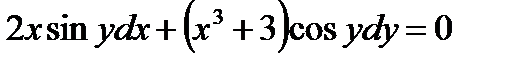 . Найти частное решение, удовлетворяющее условию
. Найти частное решение, удовлетворяющее условию 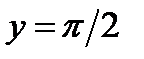 при
при 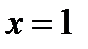 .
.
Решение. Разделим каждый член уравнения на произведение 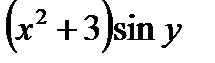 :
:
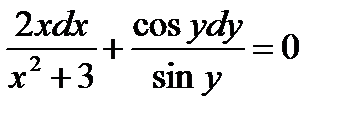 .
.
Интегрируя, находим 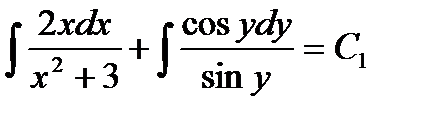 ,
, 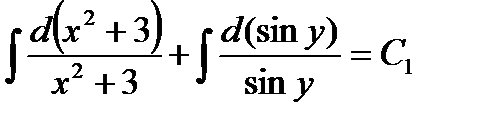 ,
, 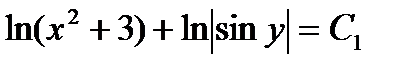 .
.
После потенцирования получим 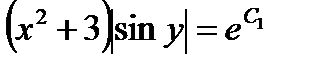 ,
, 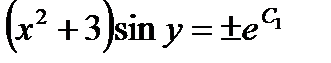 или
или 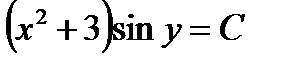 , где
, где 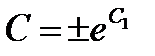 . Отсюда
. Отсюда 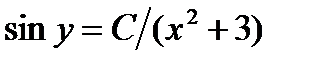 .
.
Произведение 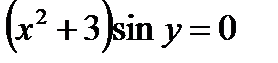 при
при 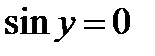 ; так как при этом значении дифференциальное уравнение не теряет числового смысла, то
; так как при этом значении дифференциальное уравнение не теряет числового смысла, то 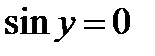 - решение уравнения. Но оно входит в интеграл
- решение уравнения. Но оно входит в интеграл 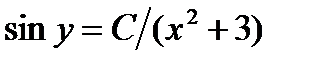 при
при 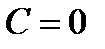 . Значит, общий интеграл уравнения имеет вид
. Значит, общий интеграл уравнения имеет вид 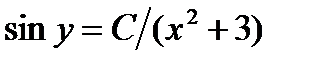 .
.
Подставив в общий интеграл значения 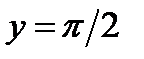 и
и 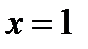 , получим
, получим 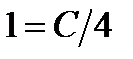 , откуда
, откуда 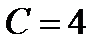 . Итак, частный интеграл уравнения, удовлетворяющий данному условию. Имеет вид
. Итак, частный интеграл уравнения, удовлетворяющий данному условию. Имеет вид 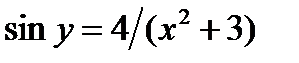 .
.
Пример 5. Решить уравнение 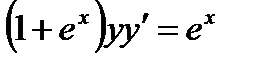 . Найти частное решение, удовлетворяющее условию
. Найти частное решение, удовлетворяющее условию 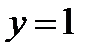 при
при 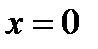 .
.
Решение. Так как 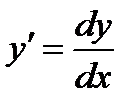 , то
, то 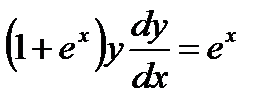 , откуда
, откуда 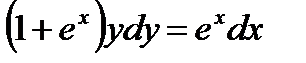 .
.
Разделим обе части уравнения на 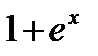 :
: 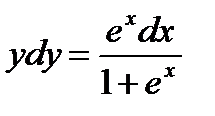 .
.
Интегрируя, находим 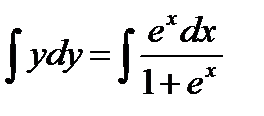 ,
, 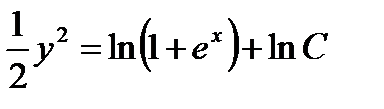 , или
, или 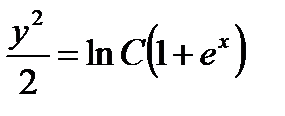 .
.
После потенцирования получим решение 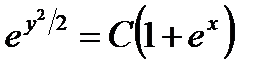 .
.
При 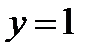 и
и 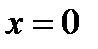 имеем
имеем 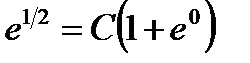 ,
, 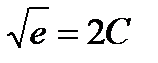 , откуда
, откуда 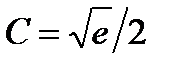 .
.
Итак, частный интеграл уравнения, удовлетворяющий данному условию, имеет вид
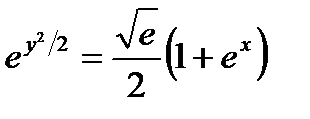 , или
, или 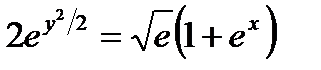 .
.
Пример 6. Решить уравнение 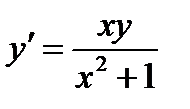 . Найти частное решение, удовлетворяющее условию
. Найти частное решение, удовлетворяющее условию 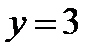 при
при 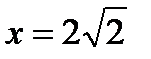 .
.
Решение. Так как 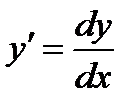 , то
, то 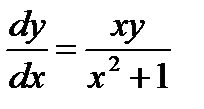 , откуда
, откуда 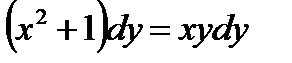 .
.
Разделим обе части уравнения на произведение 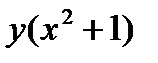 :
: 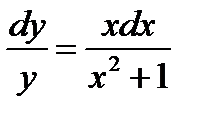 .
.
Интегрируя находим 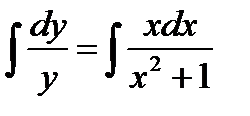 ,
, 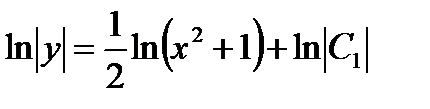 .
.
После потенцирования получим решение 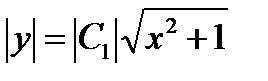 , откуда
, откуда 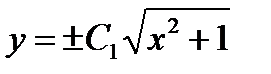 , или
, или 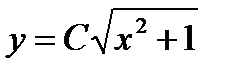 , где
, где 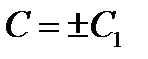 .
.
Произведение 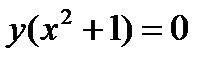 при
при 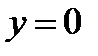 ; так как при этом значении y дифференциальное уравнение не теряет числового смысла, то
; так как при этом значении y дифференциальное уравнение не теряет числового смысла, то 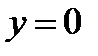 - решение уравнения. Но оно входит в решение
- решение уравнения. Но оно входит в решение 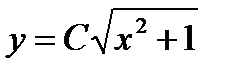 при
при 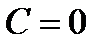 . Значит, общее решение уравнения имеет вид
. Значит, общее решение уравнения имеет вид 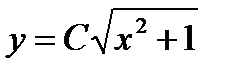 .
.
Подставив в общее решение значения 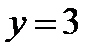 и
и 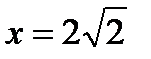 , получим
, получим 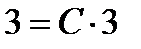 , откуда
, откуда 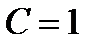 . Итак, частное решение уравнения, удовлетворяющее данному условию, имеет вид
. Итак, частное решение уравнения, удовлетворяющее данному условию, имеет вид 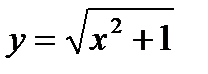 .
.
Дифференциальные уравнения второго порядка. Если дифференциальное уравнение содержит производную или дифференциал не выше второго порядка, то оно называется дифференциальным уравнением второго порядка.
Общий вид такого уравнения 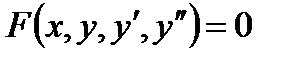 ,
,
где 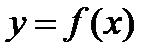 - искомая неизвестная функция,
- искомая неизвестная функция, 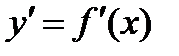 и
и 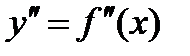 - ее производные по x первого и второго порядков, а
- ее производные по x первого и второго порядков, а 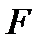 - заданная функция переменных
- заданная функция переменных 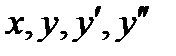 .
.
Общим уравнением дифференциального уравнения второго порядка называется функция 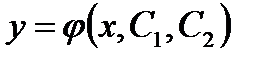 от x и двух произвольных постоянных
от x и двух произвольных постоянных 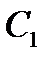 и
и 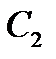 , обращающая это уравнение в тождество по x.
, обращающая это уравнение в тождество по x.
Общее решение, записанное в неявном виде 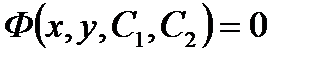 , называется общим интегралом.
, называется общим интегралом.
Частным решением уравнения 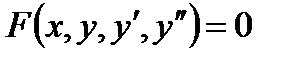 называется решение, полученное из общего решения при фиксированном значении
называется решение, полученное из общего решения при фиксированном значении 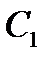 и
и 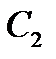 :
: 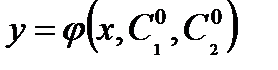 , где
, где 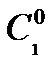 и
и 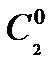 - фиксированные числа.
- фиксированные числа.
Частным интегралом этого уравнения называется интеграл, полученный из общего интеграла при фиксированном значении 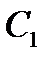 и
и 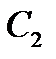 :
: 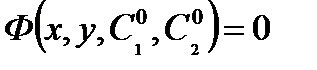 , где
, где 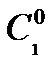 и
и 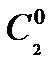 - фиксированные числа.
- фиксированные числа.
Общее решение дифференциального уравнения 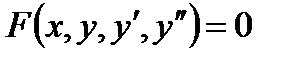 можно рассматривать кА семейство интегральных кривых данного уравнения, зависящее от двух параметров
можно рассматривать кА семейство интегральных кривых данного уравнения, зависящее от двух параметров 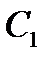 и
и 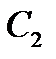 . Частному решению, полученному из общего, соответствует одна кривая этого семейства.
. Частному решению, полученному из общего, соответствует одна кривая этого семейства.
Задача Коши для дифференциального уравнения второго порядка состоит в том, чтобы найти решение, удовлетворяющее начальным условиям 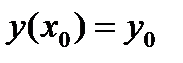 ,
, 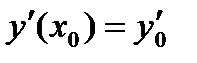 . Постоянные
. Постоянные 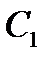 и
и 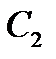 определяются из системы уравнений
определяются из системы уравнений
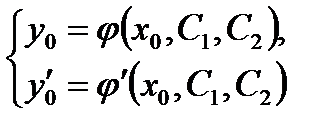
Другими словами, из всех интегральных кривых данного дифференциального уравнения требуется выделить интегральную кривую, проходящую через данную точку 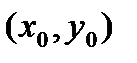 в заданном направлении
в заданном направлении 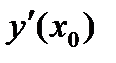
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида 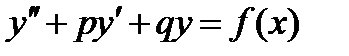 , где
, где 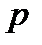 и
и 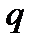 - некоторые числа.
- некоторые числа.
Если 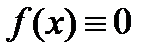 , то дифференциальное уравнение называется линейным однородным. Оно имеет вид
, то дифференциальное уравнение называется линейным однородным. Оно имеет вид 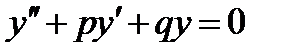 .
.
Справедлива теорема: если 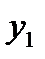 и
и 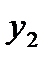 - частые решения уравнения
- частые решения уравнения 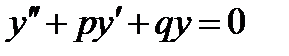 , причем
, причем 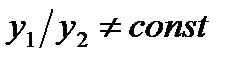 , то функция
, то функция 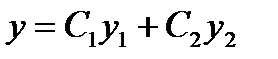 , где
, где 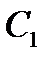 и
и 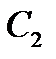 - произвольные постоянные, является общим решением этого уравнения.
- произвольные постоянные, является общим решением этого уравнения.
Решением данного дифференциального уравнения 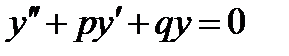 должна быть такая функция, которая, будучи подставлена в уравнение, превратит его в тождество. Левая часть уравнения представляет собой сумму функции y и ее производных
должна быть такая функция, которая, будучи подставлена в уравнение, превратит его в тождество. Левая часть уравнения представляет собой сумму функции y и ее производных 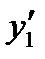 и
и 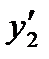 , взятых с некоторыми постоянными коэффициентами. Чтобы такая сумма бранилась в нуль, надо, чтобы y,
, взятых с некоторыми постоянными коэффициентами. Чтобы такая сумма бранилась в нуль, надо, чтобы y, 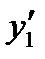 и
и 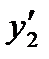 были подобны между собой.
были подобны между собой.
Такой функцией является функция 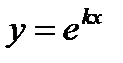 , где
, где 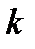 - постоянная. Требуется подобрать
- постоянная. Требуется подобрать 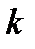 так, чтобы эта функция удовлетворяла уравнению
так, чтобы эта функция удовлетворяла уравнению 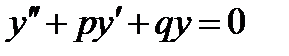 .
.
Так как 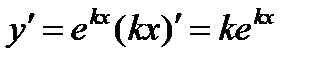 , а
, а 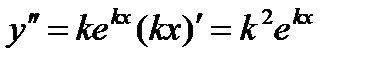 , то, подставляя эти значения y,
, то, подставляя эти значения y, 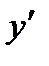 и
и 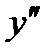 в левую часть уравнения
в левую часть уравнения 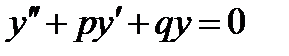 , получим
, получим 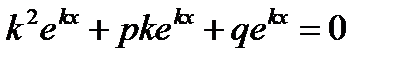 .
.
Сокращая на множитель 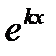 , не обращающийся в нуль, получим характеристическое уравнение
, не обращающийся в нуль, получим характеристическое уравнение 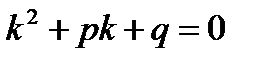 .
.
Это уравнение определяет те значения 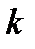 , при которых функция
, при которых функция 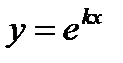 является решением дифференциального уравнения
является решением дифференциального уравнения 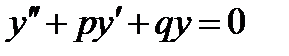 .
.
При решении характеристического уравнения 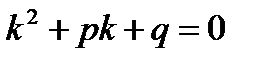 возможны три случая:
возможны три случая:
| № | корни уравнения | частные решения | общее решение |
действительные различные ( 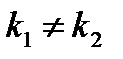 ) ) | 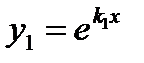 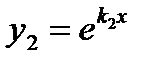 | 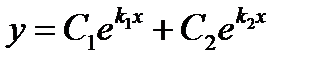 | |
действительные равные ( 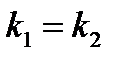 ) ) | 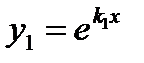 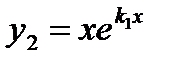 | 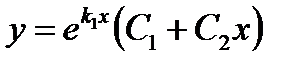 | |
комплексно-сопряженные ( 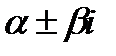 ) ) | 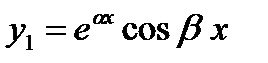 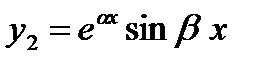 | 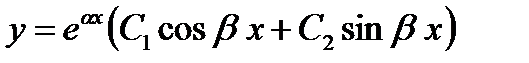 |
Пример 7. Найти общее решение дифференциального уравнения 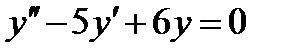 .
.
Решение. Составим характеристическое уравнение и найдем его корни:
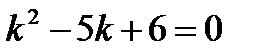 ,
, 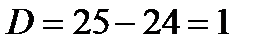 ,
, 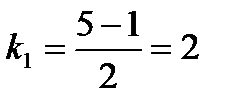 ,
, 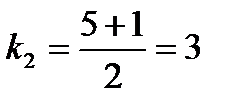 .
.
Корни характеристического уравнения являются действительными и различными. Поэтому 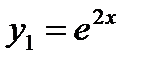 ,
, 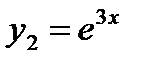 - частные решения, а
- частные решения, а 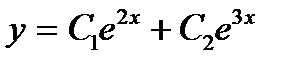 - общее решение данного дифференциального уравнения.
- общее решение данного дифференциального уравнения.
Пример 8. Найти общее решение дифференциального уравнения 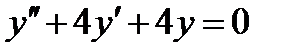 .
.
Решение. Характеристическое уравнение 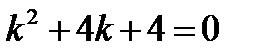 или
или 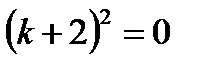 имеет действительные равные корни
имеет действительные равные корни 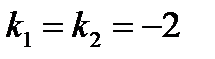 . Поэтому
. Поэтому 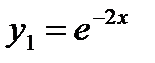 ,
, 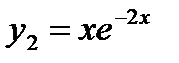 - частные решения, а
- частные решения, а 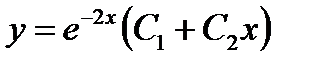 - общее решение данного дифференциального уравнения.
- общее решение данного дифференциального уравнения.
Пример 9. Найти общее решение дифференциального уравнения 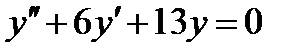 .
.
Решение. Составим характеристическое уравнение и найдем его корни:
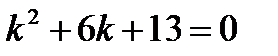 ,
, 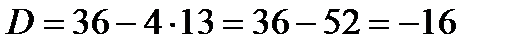 ,
, 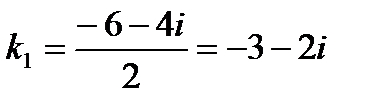 ,
, 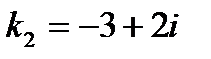 .
.
Корни являются комплексно-сопряженными. Поэтому 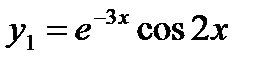 ,
, 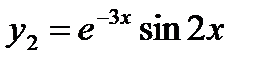 - частные решения, а
- частные решения, а 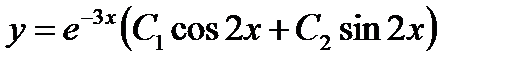 - общее решение данного дифференциального уравнения.
- общее решение данного дифференциального уравнения.
Пример 10. Найти общее решение дифференциального уравнения 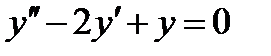 , удовлетворяющее данными начальным условиям при
, удовлетворяющее данными начальным условиям при 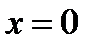 ,
, 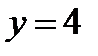 ,
, 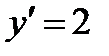 .
.
Решение. Характеристическое уравнение 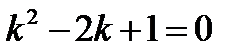 или
или 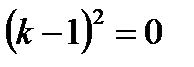 имеет действительные равные корни
имеет действительные равные корни 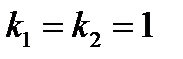 . Поэтому
. Поэтому 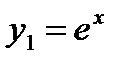 ,
, 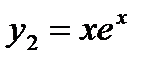 - частные решения, а
- частные решения, а 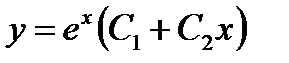 - общее решение данного дифференциального уравнения.
- общее решение данного дифференциального уравнения.
Для определения частного решения, удовлетворяющего данным начальным условиям, сначала найдем производную 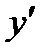 функции
функции 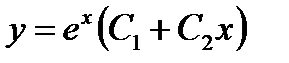 :
:
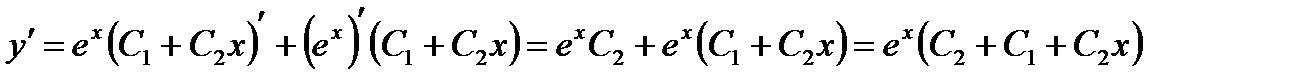 . Теперь подставим начальные условия в выражения для
. Теперь подставим начальные условия в выражения для 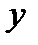 и
и 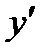 :
:
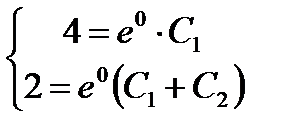
или 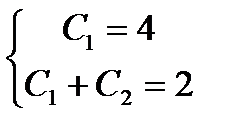 ,
,
откуда 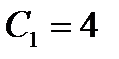 и
и 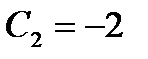 .
.
Подставив эти значения в общее решение, найдем частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям: 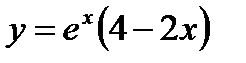 .
.
Упражнения для самопроверки
1. Найдите интегралы:
а) 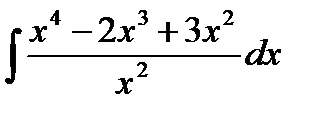 ; б)
; б) 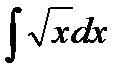 ; в)
; в) 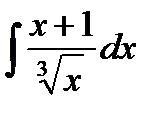 ; г) ;
; г) ; 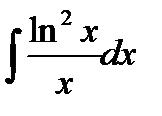 ; д)
; д) 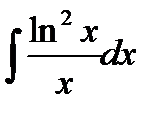 ;е)
;е) 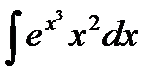 ; ж)
; ж) 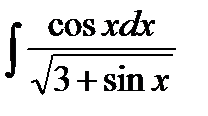 ; з)
; з) 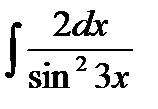 .
.
2. Вычислите определенные интегралы:
а) 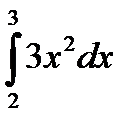 ; б)
; б) 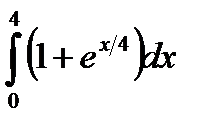 ; в)
; в) 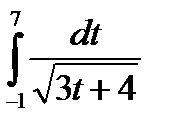 ; г)
; г) 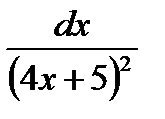 .
.
3. Решите дифференциальные уравнения и найдите частные решения (частные интегралы), удовлетворяющие данным условиям:
а) 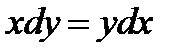 ,
, 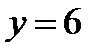 при
при 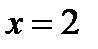 ; б)
; б) 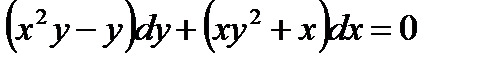 ,
, 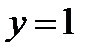 при
при 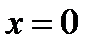 ; в)
; в) 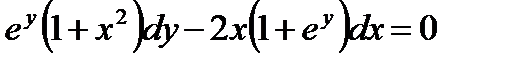 ,
, 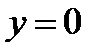 при
при 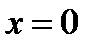 ; г)
; г) 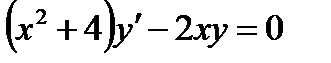 ,
, 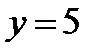 при
при
