Интегрирование дифференциального бинома

Интегралы типа 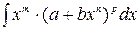, называемые интегралами от дифференциального бинома, где a и b – вещественные числа; 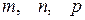- рациональные числа, берутся лишь в случае, когда хотя бы одно из чисел 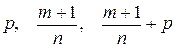является целым числом.

Приведение подынтегральной функции к рациональной осуществляется с помощью следующих подстановок:

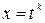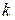1) если p – целое число, то подстановка , где -наименьшее общее кратное знаменателей дробей m и n;

2) если 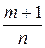- целое число, то подстановка 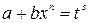, где s – знаменатель дроби p;

3) если 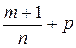- целое число, то подстановка 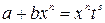, где s - знаменатель дроби p.

Во всех остальных случаях интегралы типа 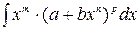не выражаются через известные элементарные функции.

Пример .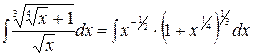

Так как 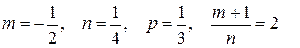, то делаем подстановку 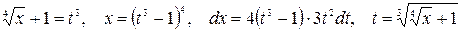. Таким образом

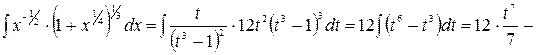
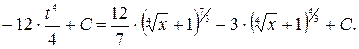
ГЛАВА 2. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ

1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ.

Пусть функция 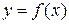определена и непрерывна на отрезке [a,b], где -∞<a<b<∞ .

1. Разобьем отрезок [a,b] произвольным образом на n частичных отрезков .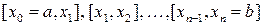

2. В каждом частичном отрезк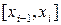е , где 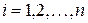, выбираем произвольным образом точку 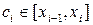и вычисляем значение функции в этой точке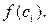

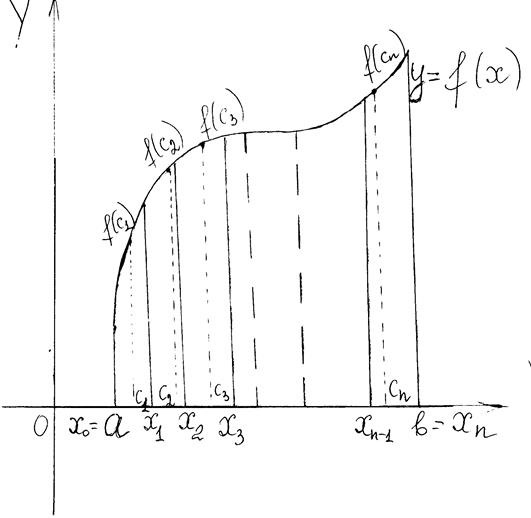
3. Умножим найденное значение функции 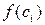на длину 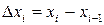соответствующего частичного отрезка, получим .

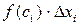4. Составим сумму 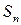всех таких произведений:

,

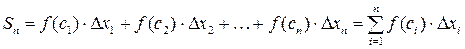которая называется интегральной суммойфункции 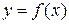на отрезке [a,b].

5. Обозначим через 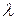длину наибольшего частичного отрезка 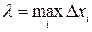, где 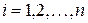. Перейдем в интегральной сумме к пределу при .

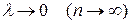Определение. Определенным интегралом функции 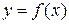на отрезке [a,b] называется предел интегральной суммы 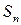, если этот предел существует, конечен и не зависит от способа составления интегральной суммы и обозначается

.

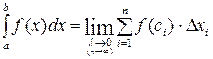Числа a и b называются соответственно нижними верхним пределами интегрирования, 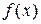- подынтегральной функцией, 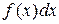- подынтегральным выражением, x – переменной интегрирования, отрезок [a,b] – отрезком интегрирования.

Имеет место следующее утверждение:

Если функция 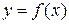непрерывна на отрезке [a,b], то определенный интеграл 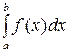существует.

Перечислим свойства определенного интеграла

1. Определенный интеграл не зависит от обозначения переменной интегрирования, т.е. .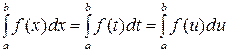

2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю: .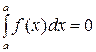

3. Для любого вещественного числа k верно, что .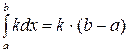

4. Аддитивность по функции: если функци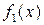и и 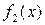интегрируемы на [a,b], тогда интегрируема на [a,b] и их сумма

.

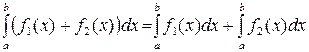5. Аддитивность по области: если функция 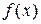интегрируема на [a,b] и a<c<b, то .

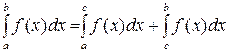(Заметим, что это свойство верно и в случае )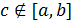

6. «Теорема о среднем». Если функция 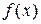непрерывна на отрезке [a,b], то существует точка 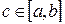такая, что

.

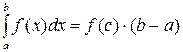Доказательство:

Пусть 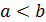и m, M - наименьшее и наибольшее значение функции f(x) на промежутке [a,b]. Тогда по свойству 10 (оценка интегралов) имеем

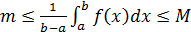. Обозначим 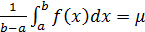, где

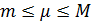. Так как f(x) непрерывна, следовательно, по свойству непрерывных функций 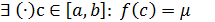, следовательно,

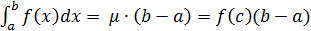ч.т.д.

7. Если функция 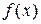неотрицательна на отрезке [a,b], где a<b, то интеграл 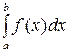имеет тот же знак, что и функция, т.е. .

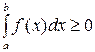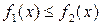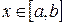8. Если при , то

.

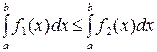9. Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции: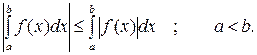

10. Оценка интеграла. Если m и M – соответственно наименьшее и наибольшее значения функции 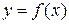на отрезке [a,b], (a<b), то

.

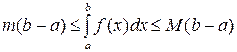11. При перестановке местами пределов интегрирования знак определенного интеграла меняется на противоположный

.

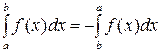12. Интеграл по симметричному промежутку от нечетной функции равен нулю, т.е. если 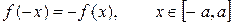, то .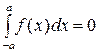

13. Интеграл по симметричному промежутку от четной функции равен удвоенному интегралу от этой функции по половине промежутка, т.е. если 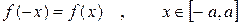, то 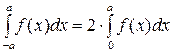.