Интегрирование дробно-рациональных функций.

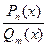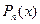Определение. Дробно-рациональной функцией называется функция вида , где и 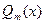- многочлены степени m и n, соответственно.

Если степень числителя меньше степени знаменателя, дробь называется правильной, в противном случае, дробь называется неправильной.

Всякая неправильная дробь в результате деления числителя на знаменатель может быть представлена в виде суммы многочлена 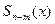и правильной рациональной дроби 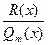. Например,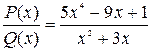

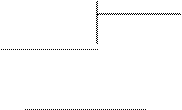
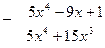
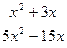
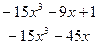
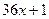
Разделив числитель на знаменатель в столбик, мы можем представить заданную неправильную дробь в виде многочлена, записанного под чертой делителя, и правильной рациональной дроби, у которой в числителе будет стоять многочлен, являющийся остатком деления числителя на знаменатель, т.е. .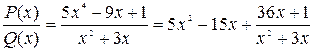

Правильные рациональные дроби вида

I) ;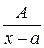

II)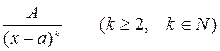

III) 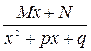, ( знаменатель – квадратный трехчлен с отрицательным дискриминантом ( 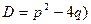, т.е. имеет комплексные корни);

IV) 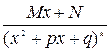, ( 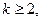и знаменатель имеет комплексные корни),

где 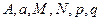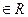, называются простейшими рациональными дробями I, II, III, IV типов.

Рассмотрим интегрирование простейших дробей I-III типов :

I.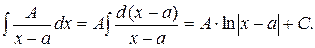

II.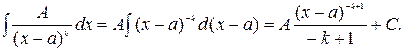

III.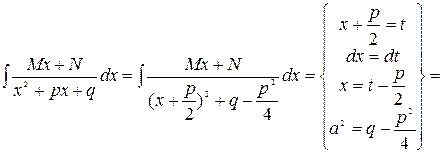

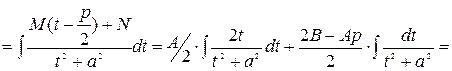
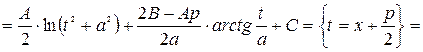
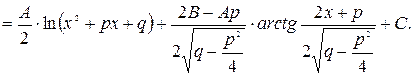
Интегрирование простейшей дроби IV типа будет показано далее на конкретном примере.

Пример.

1.

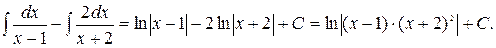
2.

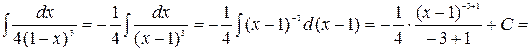
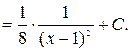
3.

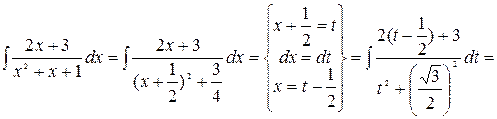
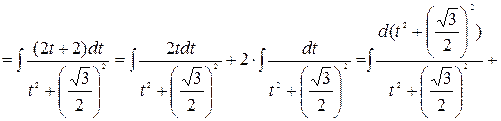
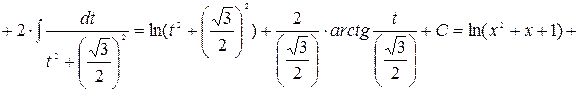
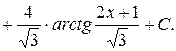
Рассмотрим пример на интегрирование простейших дробей IV типа.

4.

.

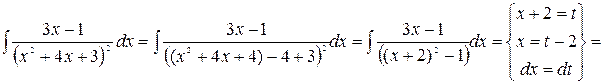
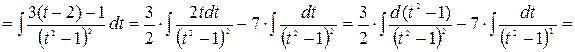
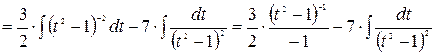Рассмотрим более подробно вычисление последнего интеграла

=

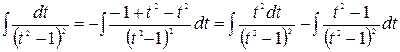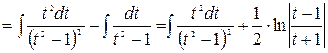
Для вычисления последнего интеграла применим метод интегрирования по частям:

.

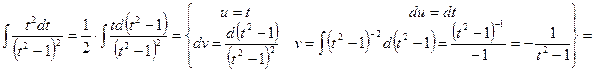
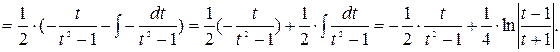Объединяя все найденные результаты, получаем

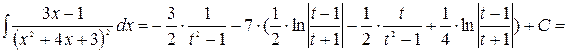
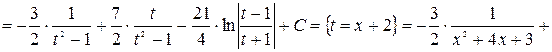
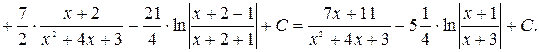
5.

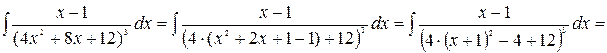
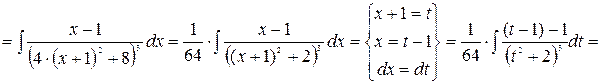
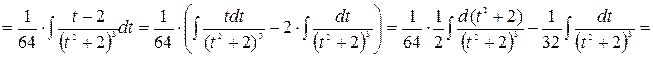
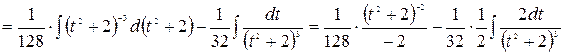
Рассмотрим последний интеграл

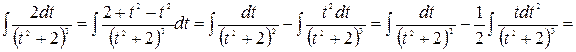
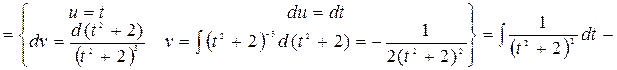
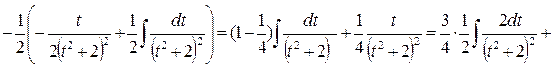
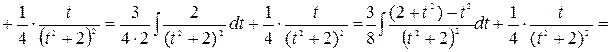
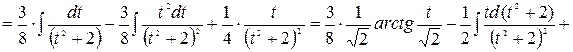
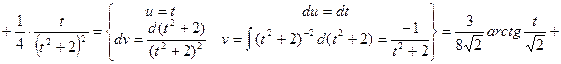
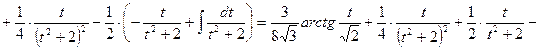
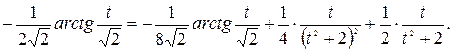
Объединяя полученные результаты, получаем

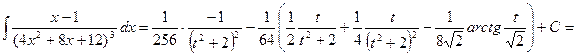
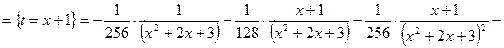
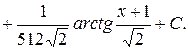
Алгоритм интегрирования рациональных дробей

1. Выделить правильную рациональную дробь (степень многочлена числителя меньше степени многочлена знаменателя), если исходная дробь неправильная.

2. Разложить знаменатель правильной рациональной дроби на линейные и квадратичные сомножители (в соответствии с теоремой о разложении многочлена).

3. Разложить правильную рациональную дробь на простейшие в соответствии с корнями знаменателя.

4. Проинтегрировать целую часть (многочлен) и простейшие дроби.

Разложение правильной рациональной дроби можно проводить двумя способами.

Рассмотрим первый из них (метод частных значений ) на конкретном примере.

Пример. Разложить данную дробь на простейшие.

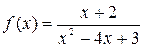
Эта дробь правильная, так как степень числителя равна 1, а степень знаменателя равна 2, следовательно, целую часть выделять не требуется. Приравняем знаменатель дроби к нулю и найдем его корни

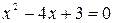
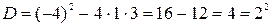
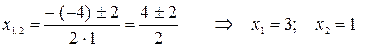
Напомним, что если корнями квадратного трехчлена 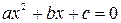являются значения 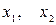, то имеет место формула

.

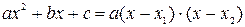Таким образом, знаменатель исходной дроби может быть представлен в виде 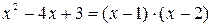,следовательно, сама дробь будет разложена на две простейшие дроби

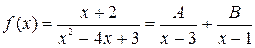, где А и В являются неопределенными коэффициентами, подлежащими определению.

Приведем правую часть равенства к общему знаменателю, получим

.

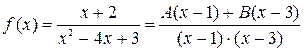Так как знаменатели левой и правой дроби равны и между дробями стоит знак равенства, то равны и числители этих дробей. Отсюда имеем:

.

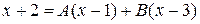Метод частных значений заключается в том, что в левую и правую части полученного равенства, содержащего А и В, подставляют значения, равные корням знаменателя исходной дроби.

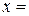
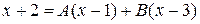
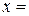1

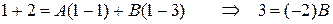
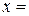3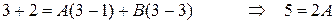

Таким образом,

Подставляя найденные значения в разложение исходной дроби на простейшие, получаем

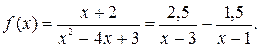
Метод частных значений рекомендуется применять в тех случаях, когда знаменатель дроби раскладывается либо на линейные множители, либо на линейные множители и один квадратный трехчлен с отрицательным дискриминантом. В последнем случае надо учитывать, что корней знаменателя будет не достаточно для нахождения всех неопределенных коэффициентов, следовательно, потребуются еще 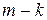произвольныx значений x, где m – степень знаменателя.

Пример Разложить на простейшие дроби функцию

.

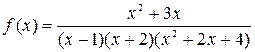В данном примере знаменатель представляет собой произведение двух линейных множителей и одного квадратного трехчлена с отрицательным дискриминантом, следовательно

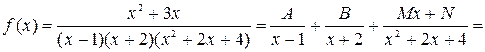
После приведения к общему знаменателю получаем новую дробь вида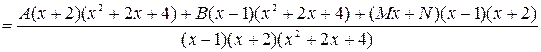

Так как все дроби связаны между собой знаками равенства и имеют одинаковый знаменатель, то числитель исходной дроби равен числителю последней, т.е.

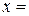
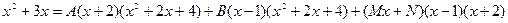
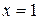
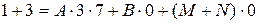
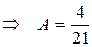
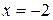
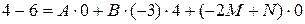
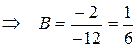
Так как корней уравнения больше нет, а неопределенными остались два коэффициента, то выбираем произвольным образом еще два значения x, например 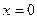и .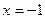

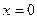
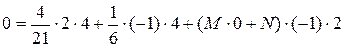
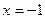
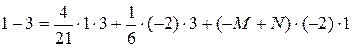
Объединяя два последних выражения в систему, получим

.

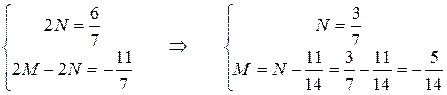Подставляя найденные коэффициенты в выше стоящее разложение, получаем, что .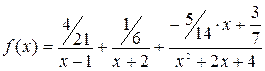

Второй метод нахождения неопределенных коэффициентов при разложении на простейшие дроби заключается в сравнении коэффициентов при одинаковых степенях x в многочленах, стоящих в числителях исходной и полученной дробей. Результаты сравнения записываются в виде системы линейных уравнений, решая которую и находят значения неопределенных коэффициентов.

Пример Вычислить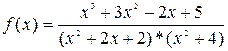

При разложении этой функции на простейшие дроби нужно учитывать, что в знаменателе стоят два квадратных трехчлена с отрицательным дискриминантом, поэтому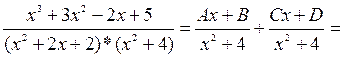

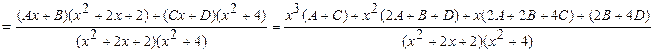
Так как числители между собой равны, то составляем систему, приравнивая коэффициенты при одинаковых степенях многочленов

, .

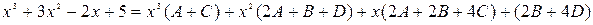
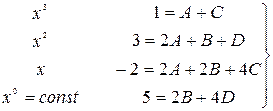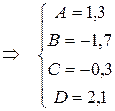Таким образом, .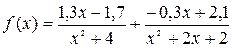

Приведем еще несколько примеров стандартных интегралов дробно-рациональных функций, у которых знаменатель – квадратный трехчлен с отрицательным дискриминантом:

;

.

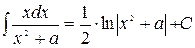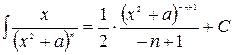
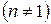А теперь рассмотрим случай интегрирования дробно-рациональной функции, у которой степень числителя больше степени знаменателя (т.е. n>m).

Пример.

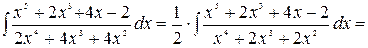
так как степень числителя n=5, а степень знаменателя m=4, то эта дробь неправильная и необходимо выделить целую часть этой дроби:

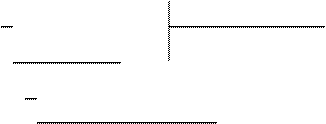
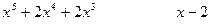(целая часть)

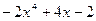
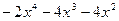
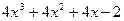(остаток)

Следовательно, данный интеграл равносилен следующему

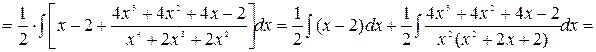
Разложим подынтегральную функцию последнего интеграла на простейшие дроби

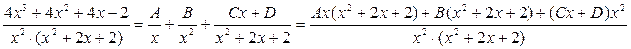
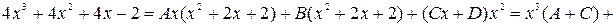
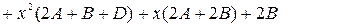
Сравнивая коэффициенты при одинаковых степенях в левой и правой частях, получаем систему линейных уравнений

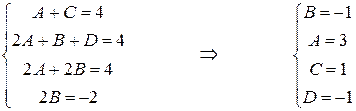
Учитывая значения найденных коэффициентов, заменяем подынтегральную функцию последнего интеграла разложением на простейшие

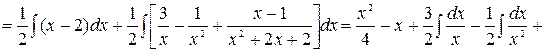
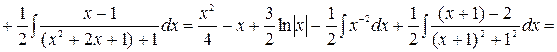
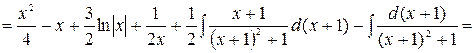
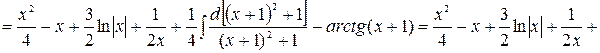
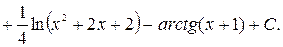
Заметим, что аргумент последнего логарифма является квадратным трехчленом с отрицательным дискриминантом, который принимает только положительные значения, поэтому модуль был заменен на обычные скобки.

Интегралы вида 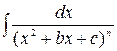после выделения в знаменателе полного квадрата приводятся к интегралам вида 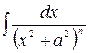, берущимся с помощью тригонометрических подстановок, которые будут рассмотрены далее.