ПРАКТИКА № 9. Несобственный интеграл.
Задача 2. Вычислить несобственный интеграл 1 рода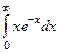 
.
Ответ.1.
Задача 7.Выяснить сходимость несобственного интеграла по признакам сравнения: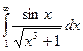 
, не вычисляя его.
Ответ. Сходится.
Задача 8.Выяснить сходимость несобственного интеграла по признакам сравнения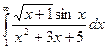 
не вычисляя его.
Ответ.Сходится.
Задача 9.Выяснить сходимость несобственного интеграла 2-го рода по признакам сравнения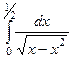 
.
Ответ.Сходится.
Задача 10.Выяснить сходимость несобственного интеграла 2-го рода по признакам сравнения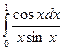 
.
Ответ.Расходится.
Задача 11.Выяснить сходимость несобственного интеграла по признакам сравнения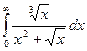 
.
Ответ.Сходится.
Задача 12.Вычислить несобственный интеграл 2 рода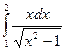 
.
Ответ.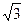 
.
Задача 13. Вычислить несобственный интеграл 2 рода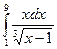 
.
Ответ.25,2.
ПРАКТИКА № 10.
Задача 2. Вычислить двойной интеграл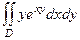 
, где D квадрат, 
.
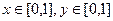Ответ.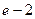 
.
Задача 4. Вычислить интеграл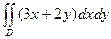 
по треугольнику D, вершины которого: (0,0),(1,1),(1,2).
Ответ. 2.
Задача 5.Сменить порядок интегрирования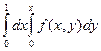 
.
Ответ.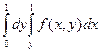 
.
ПРАКТИКА № 11.
Задача 1. Изменить порядок интегрирования: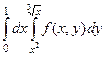 
.
Ответ.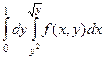 
.
Задача 2. Сменить порядок интегрирования в двойном интеграле:
.
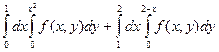Ответ.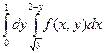 
.
Задача 3. Изменить порядок интегрирования: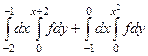 
.
Ответ.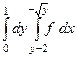 
.
Задача 4.Вычислить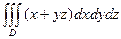 
по кубу 
.
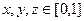Ответ.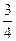 
.
Задача 5. Вычислить тройной интеграл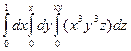 
.
Ответ.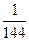 
.
Задача 6. Найти объём тела, ограниченного поверхностями: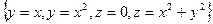 
.
Ответ.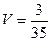 
.
Задача 8. Вычислить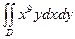 
, где D - четверть круга радиуса 1 (в первой координатной четверти).
Ответ.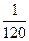 
.
ПРАКТИКА № 12.
Задача 1. Записать в полярных координатах двойной интеграл по треугольнику с вершинами (0,0), (1,0), (1,1).
Ответ.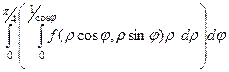 
.
Задача 2. Найти площадь поверхности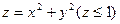 
.
Ответ.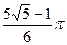 
.
Задача 3. Вычислить объём тела, ограниченного цилиндром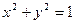 
и двумя плоскостями 
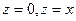в цилиндрических координатах.
Ответ.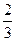 
.
Задача 4.Вычислить определитель Якоби сферических координат.
Ответ.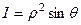 
.
Задача 5. Плотность вещества в шаре радиуса 1 равна расстоянию от начала координат. Вычислить массу (в сферических координатах).
Ответ.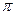 
.
Задача 5-Б. Вычислить массу шара радиуса 1, если плотность равна квадрату расстояния от центра шара.
Ответ.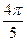 
.
Задача 6.Найти объём тела, ограниченного конусом
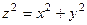и сферой радиуса 
.
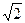Ответ.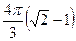 
.
Задача 7.Найти объём тела, ограниченного поверхностями
.
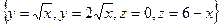Ответ.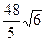 
.
ПРАКТИКА № 13.
Задача 3.Решить дифференциальное уравнение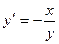 
.
Ответ.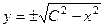 
.
Задача 4. Решить уравнение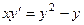 
, и найти частное решение задачи Коши: 
.
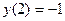Ответ. Общее решение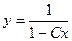 
, частное решение: 
.
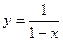ПРАКТИКА № 14.
Задача 1. Решить уравнение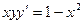 
.
Ответ.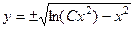 
.
Задача 2. Решить уравнение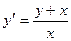 
.
Ответ.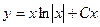 
.
Линейные уравнения 1 порядка.
Задача 3.Решить уравнение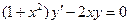 
.
Ответ.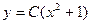 
.
Задача 4. Решить уравнение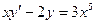 
Ответ. 
.
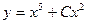Задача 5.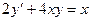 
. Ответ. 
.
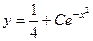Уравнения Бернулли.
Задача 6. Решить дифференциальное уравнение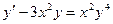 
Ответ.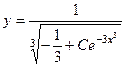 
.
Дифференциальные уравнения высшего порядка.
Задача 7. Решить дифференциальное уравнение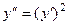 
.
Ответ.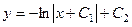 
.
Задача 8. Найти общее решение уравнения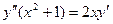 
и частное решение при условиях Коши: 
.
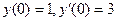Ответ.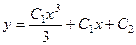 
, 
.
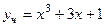Задача 9. Найти общее решение уравнения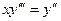 
и частное решение при условиях Коши: 
.
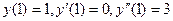Отвт.Общее реш.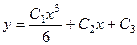 
, частное 
.
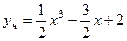ПРАКТИКА № 15.
Задача 4. Найти общее решение дифф. уравнения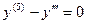 
.
Ответ.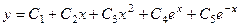 
.
Задача 5.Найти частное решение дифференциального уравнения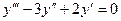 
при условиях Коши: 
.
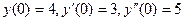Ответ.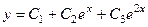 
, частное реш. 
.
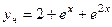Задача 6. Найти частное решение дифференциального уравнения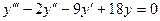 
при условиях Коши: 
.
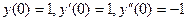Ответ.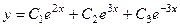 
, 
.
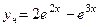Задача 9. Найти общее решение дифф. уравнения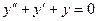 
.
Ответ.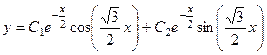 
.
Задача 10. Уравнение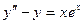 
решить методом Лагранжа
Ответ.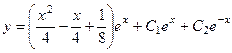 
.
ПРАКТИКА № 16.
Задача 2. Решить уравнение: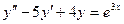 
методом неопределённых коэффициентов.
Ответ.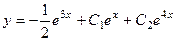 
.
Задача 3.Решить уравнение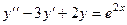 
.
Ответ.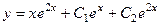 
.
Задача 4.Решить уравнение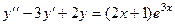 
.
Ответ.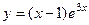 
.
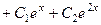Задача 5. Решить уравнение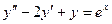 
.
Ответ.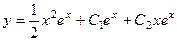 
.
Задача 6. Решить уравнение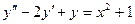 
методом неопределённых коэффициентов.
Ответ.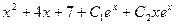 
.
Задача домашняя. Решить уравнение.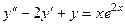 
.
Ответ.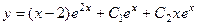 
.
ПРАКТИКА № 17
Задача 6. Вычислить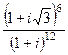 
Ответ. 
.
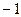Задача 7. Вычислить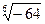 
. Ответ. 
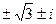и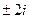 
.
Задача 9. Дано: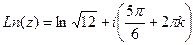 
. Найти 
.
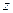Ответ.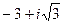 
.
Задача 10. Найти все значения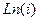 
.
Ответ.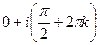 
.